a()+o(r) 5(1)本 1(t) a() () xa(t) a(t)-o(t) 图1-16随机过程的数学期望和均方差
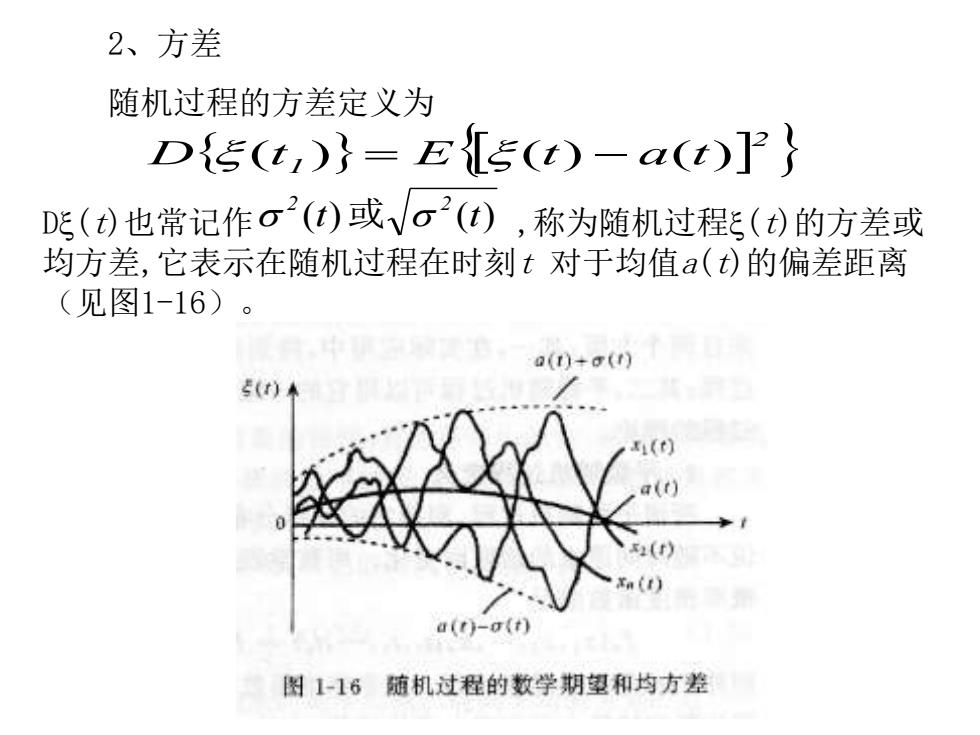
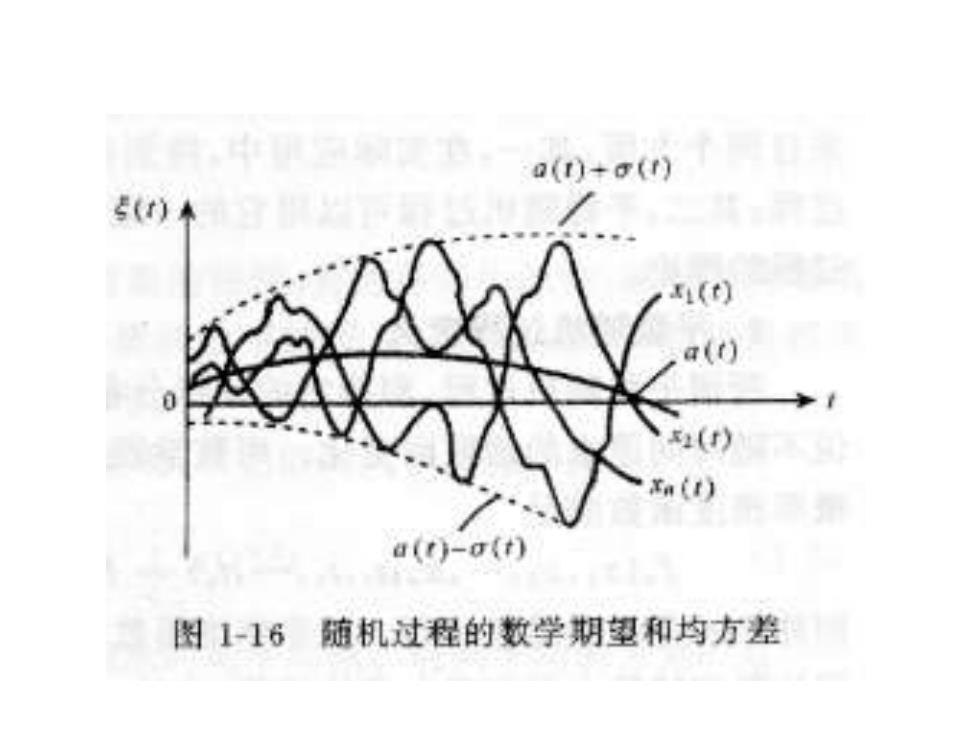
2、方差 随机过程的方差定义为 D{5(t,)}=E5(t)-a(t)]P} D()也常记作o2(0)或√o2(),称为随机过程(t)的方差或 均方差,它表示在随机过程在时刻t对于均值a(t)的偏差距离 (见图1-16)。 a()+g()】 5()米 1(t) a(t) a(t)-o(t) 图1-16随机过程的数学期望和均方差
2、方差 随机过程的方差定义为 2 1 D x (t ) = E x (t) − a(t) Dx(t)也常记作 ,称为随机过程x(t)的方差或 均方差,它表示在随机过程在时刻t 对于均值a(t)的偏差距离 (见图1-16)。 (t) 2 (t) 2 或

3、协方差函数和相关函数 数学期望以a(t)和方差o(t)描述了随机过程在各个孤立 时刻的特征,但没有反映随机过程不同时刻之间的内在联系。 协方差函数C(t,t)和相关函数R(t,t)就是用来衡量随机过 程中任意两个时刻上获得的随机变量的统计相关特性的。 协方差函数定义为 C(t,t2)=E5(t,)-a(t,)]l[5(t2)-a(t2)] 5 [x-a(t )x-a(t )f(xx)ddx 其相关函数定义为 R(t1,t2)=E{5(t,)5(t2)} [x,-a(t,)Ix2-a(t2)lfz (x1x2:t1.t2)dx,dx
3、协方差函数和相关函数 数学期望以a(t)和方差 描述了随机过程在各个孤立 时刻的特征,但没有反映随机过程不同时刻之间的内在联系。 协方差函数C(t1,t2) 和相关函数R(t1,t2)就是用来衡量随机过 程中任意两个时刻上获得的随机变量的统计相关特性的。 协方差函数定义为 (t) 2 1 1 2 2 2 1 2 1 2 1 2 1 2 1 1 2 2 x a t x a t f x x t t dx dx C t t E t a t t a t ( ) ( ) ( , ; , ) ( , ) ( ) ( ) ( ) ( ) = − − = − − − − x x 其相关函数定义为 1 1 2 2 2 1 2 1 2 1 2 1 2 1 2 x a t x a t f x x t t dx dx R t t E t t ( ) ( ) ( , ; , ) ( , ) ( ) ( ) = − − = − − x x

C(tpt)和R(t,t)之间的关系式为 C(t,t2)=E5(t)-at]+at)at2)-5(t)at2)-5t)at,)} =E5(t,)5t,)+Ea(t,)at2-E5t,)at)-E5t,)5(t)E5(2)at,》 =R(t,t2)-a(t1)a(t2) 上面的C(tpt)及R(tt)是衡量同一个随机过程,因此, 又分别称为自协方差函数和相关函数。 如果把上述概念推广到两个或更多随机过程中去,可的互 协方差函数和互相关函数。设(t)和n(t)分别表示两个随机过 程,则互协方差函数定义为 Cs.n(4,t2)=E5(t)-a(小72)-a,(t2)} 而相关函数定义为 Rs.n(t1,t2)=E[5(t,)7(t2)]
C(t1,t2)和 R(t1,t2)之间的关系式为 ( , ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( , ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 2 1 2 1 2 1 2 1 2 1 2 2 1 1 2 1 1 1 2 1 2 2 1 R t t a t a t E t t E a t a t E t a t E t t E t a t C t t E t a t a t a t t a t t a t = − = + − − = − + − − x x x x x x x x x 上面的C(t1,t2)及 R(t1,t2)是衡量同一个随机过程,因此, 又分别称为自协方差函数和相关函数。 如果把上述概念推广到两个或更多随机过程中去,可的互 协方差函数和互相关函数。设x(t)和h(t)分别表示两个随机过 程,则互协方差函数定义为 Cx ,h (t 1 ,t 2 ) = Ex (t 1 ) − ax (t 1 )h(t 2 ) − ah (t 2 ) 而相关函数定义为 ( , ) ( ) ( ) , 1 2 1 2 R t t E x t h t x h =

随机过程的统计特性一般都与时刻t和t有关。如果t2〈t, 可令t2=t,+t,则相关函数R(t,t2)可表示为R(t,t2 +),这说明相关函数依赖于起始时刻(或时间起点)t,及时 间间隔τ,及相关函数是t和x的函数。 三、平稳随机过程 平稳随机过程的重要性来自两个方面:其一,在实际应用 中,特别在通信中所遇到的过程大多属于或很接近平稳随机过 程;其二,平稳随机过程可以用他的一维、二维统计特征很好 地描述。 1、平稳随机过程定义 所谓平稳随机过程,即指它的n维分布函数或概率密度函 数不随时间的平移而变化。 fn(x1,x2,…xnt1,t2,…tn) =fn(x,x2,…xnt,+h,t2+h,…tn+h) (1-47)
随机过程的统计特性一般都与时刻t1和t2有关。如果 , 可令t2 = t1 +,则相关函数R (t1,t2)可表示为R (t1,t2 +),这说明相关函数依赖于起始时刻(或时间起点)t1及时 间间隔,及相关函数是t1和的函数。 2 1 t t 三、平稳随机过程 平稳随机过程的重要性来自两个方面:其一,在实际应用 中,特别在通信中所遇到的过程大多属于或很接近平稳随机过 程;其二,平稳随机过程可以用他的一维、二维统计特征很好 地描述。 1、平稳随机过程定义 所谓平稳随机过程,即指它的n维分布函数或概率密度函 数不随时间的平移而变化。 ( ) ( , , ; , , ) ( , , ; , , ) 1 47 f x x x t h t h t h f x x x t t t n 1 2 n 1 2 n n 1 2 n 1 2 n − = + + +