
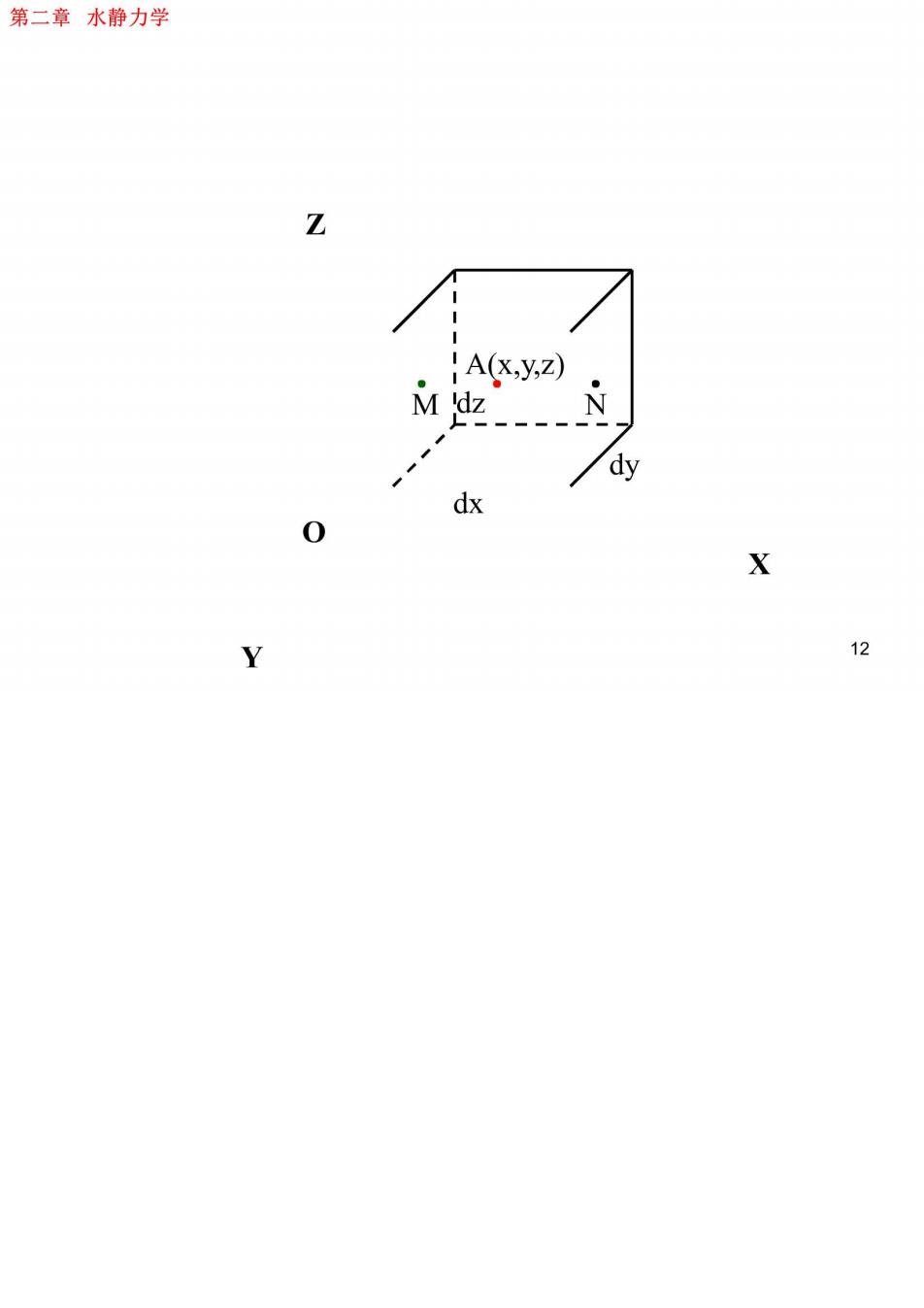
第二章水静力学 §2-2 液体平衡微分方程及其积分 一、液体平衡微分方程式 在静止流体中任取一边长为d,d和dz的微元 平行六面体的流体微团,如图所示。现在来分析作用在 这流体微团上外力的平衡条件。下面分析作用在六面 体上的表面力和质量力。 由上节所述流体静压力的特性知,作用在微元平行六 面体的表面力只有静压力。设微元平行六面体中心点处的 静压强为,则作用在六个平面中心点上的静压强可按泰 勒(G.L.Taylor)级数展开,例如:在平行于x轴的左、右 两个平面中心点上的静压强分别为:
第二章水静力学 A(x,y,Z) M dx 0 X

第二章水静力学 A点的压强为一函数p(x,y,Z) A(xy M点的坐标:Mx 0 dx 用泰勒级数展开为: X Px=px-y =( +(++( )2 忽略二阶以上微量 13

第二章水静力学 则:M点压强为: 1卫k p,(0= A(x.Y.z 20x ML应 N点压强为: 0 X p,=P+2=p+}2 =p+ 20x 20x 六面体左右两面的表面力为: p dx)dydz M点所在面为:(P2x N点所在面为:(p+)2dkd 20

第二章水静力学 另外作用在微小六面体上的质 量力在X轴向的分量为: A dx X.p dxdydz 根据平衡条件上述各力在X轴上的投影应为零,即: p爱e-p片费a+X.dd=-0 整理得:X-p=0 p Ox 同理,在x,y方向上可得: 15