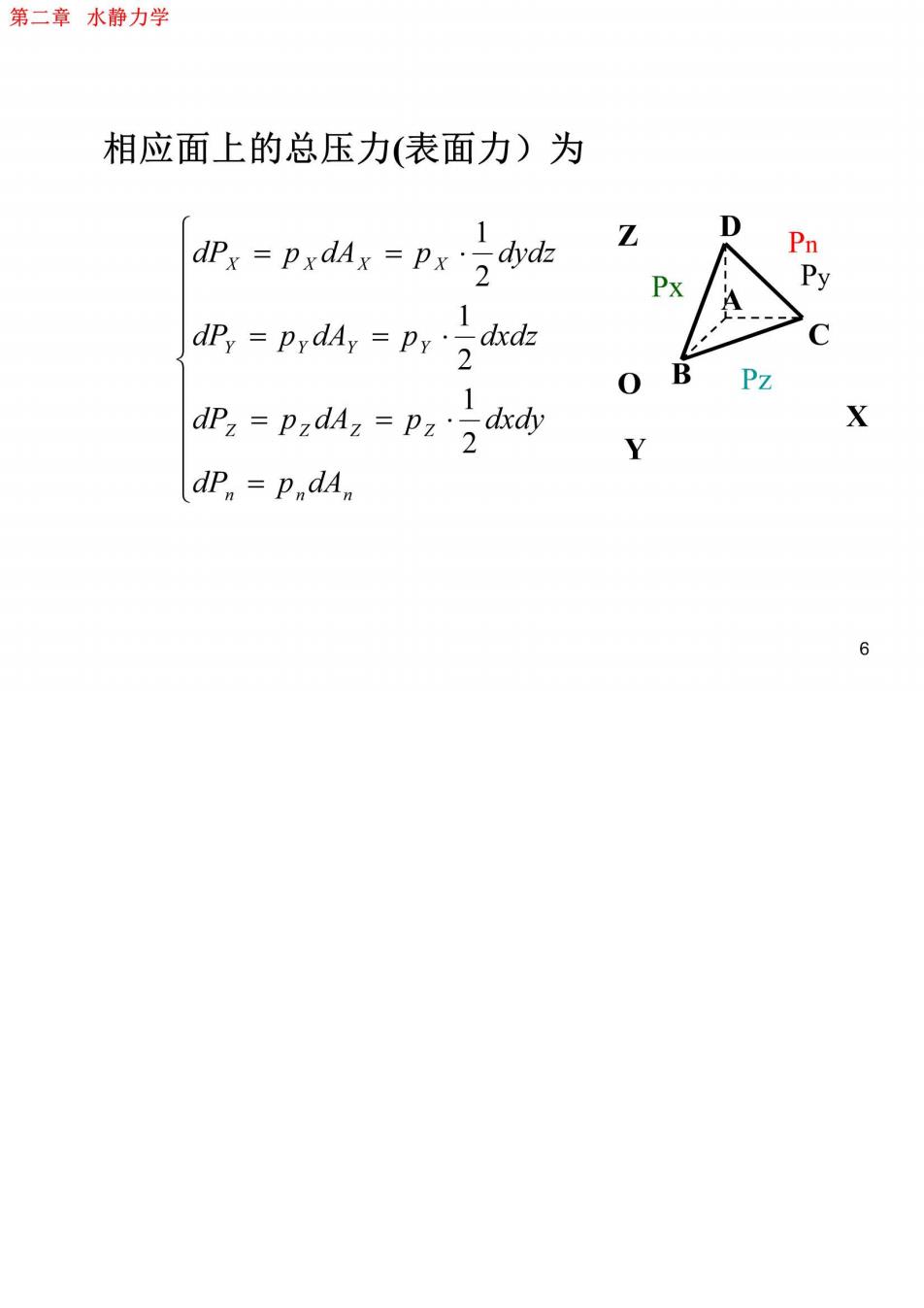
第二章水静力学 相应面上的总压力(表面力)为 1 D dPx =PxdAx =Pxdbyd Pn Px Py A dPy =pydAy =Py 2 0 B 1 dP,=PzdAz=Pz‘2d dpn=pdAn 6

第二章水静力学 D 四面体的体积△V为 av-6dkwk O B Pz X 总质量力在三个坐标方向的投影为 FxP乐X Fy=-p.dccd.y 6 rP少4口 >

第二章水静力学 D 按照平衡条件,所有作用于微 小四面体上的外力在各坐标轴上 P 投影的代数和应分别为零 Pz ΣF=0,得P-P.cos(n,x)+F,=0 ΣF,=0,得P-P.cos(n,)+F,=0 ΣF,=0,得P.-Pcos(m,z)+F.=0 以x方向为例: PxdAx-p,d4.cos(n.X)+Xpxdrdydz=0 6

第二章水静力学 0 Px 因为d4,cosn,X)=d4,=dh 2 O B PZ 代入上式得: 十 2Ay-Az-p,-2AyAzD,+Ax-Ay-Ap=0 6 1 整理后,有p,-P,+3△xpX=0 当四面体无限缩小到A点时,△x0因此: p.=P 同理,我们可以推出: 乃=Pn和p=p

第二章水静力学 D 这样我们可以得到: Py P=卫=P.=P B 上式表明任一点的静水压强 卫是各向等值的,与作用面的方 位无关。第二特性得到证明。 但液体中不同点上的静水压强可以不等