《物理化学》课程教学课件（PPT讲稿）第二章 热力学第二定律

$2.4熵的概念def8Q.AS:二T0判据（密闭系统）：AS≥T熵增大原理（孤立系统）：△S≥0“在孤立系统中所发生的过程总是向着炳增大的方向进行26

26 §2.4 熵的概念 def Qr S T   =  熵判据(密闭系统)： Q S T   熵增大原理(孤立系统)：   S 0 “在孤立系统中所发生的过程总是向 着熵增大的方向进行

一、可逆过程热温商：Q1Q2=0对于卡诺循环：TT2%证明任意可逆循环=027

27 一、可逆过程热温商： Q Q T T 1 2 1 2 + = 0  =0 i i T Q 对于卡诺循环： 证明任意可逆循环：

证：任意可逆循环可以被许多绝热可逆线和定温可逆线分割成许多小卡诺循环而每个小卡诺循环的热温商之和为零808060=ZpTT1 T,相邻两个小卡诺循环的绝热可逆线抵消：当折线段趋于无穷小时80;S0.pZ=0VTT,28

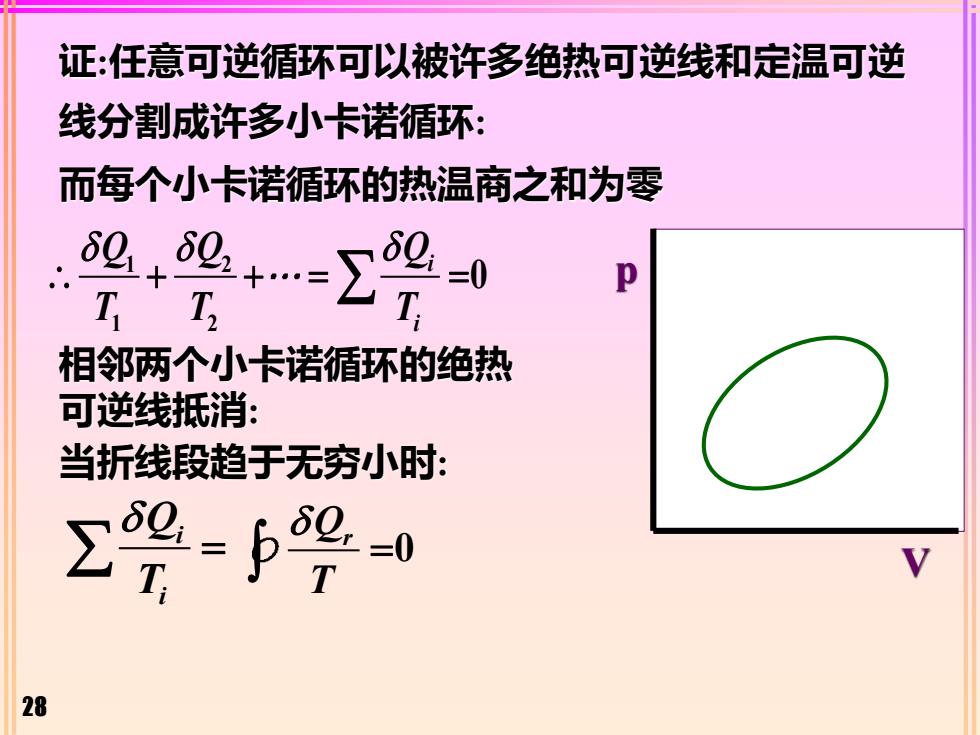
28 p V 证:任意可逆循环可以被许多绝热可逆线和定温可逆 线分割成许多小卡诺循环: i i Q Q Q T T T 1 2 1 2 0     + + = =  i i Q T   = Qr T 0  =  相邻两个小卡诺循环的绝热 可逆线抵消: 而每个小卡诺循环的热温商之和为零 当折线段趋于无穷小时:

二、炳BαA→B→A假设将任意可逆循环过程看作%-(%) +(%)p=0一TaeB(%) --1(%) - (%)β其积分值与途径无关VdefL808Qrdef或dsAS=S.-S,==TT单位：J·K-1，容量性质29

29 二、熵 单位：JK-1 ， 容量性质 A B A   假设将任意可逆循环过程看作 → → B A r r r A B Q Q Q T T T 0          = + =            B A r r A B Q Q T T         = −           其积分值与途径无关 def B r B A A Q S S S T   = − =  def Qr dS T  或 = p V A B   B r A Q T     =     

三、不可逆过程的热温商9+9<0根据卡诺定理，≤nRTT2A.<0任意不可逆循环过程α（不可逆）和β（可逆）8Q.(9 (% pZ<0αBAB(% -1 (%)ZB-TABA80.1→BSA二V78Q8Q;Z则 △A→BS>或dsTTAB30

30 三、不可逆过程的热温商 根据卡诺定理，I  R Q Q T T 1 2 1 2 +  0 i i Q T  0 则 或 A i r B A B Q Q T T 0     →     +            A i r B A B Q Q T T     →      −           i A B A B Q S T  → →          Qi dS T   任意不可逆循环过程 (不可逆)和 (可逆) B r A B A Q S T   →   = =       p  B  A V