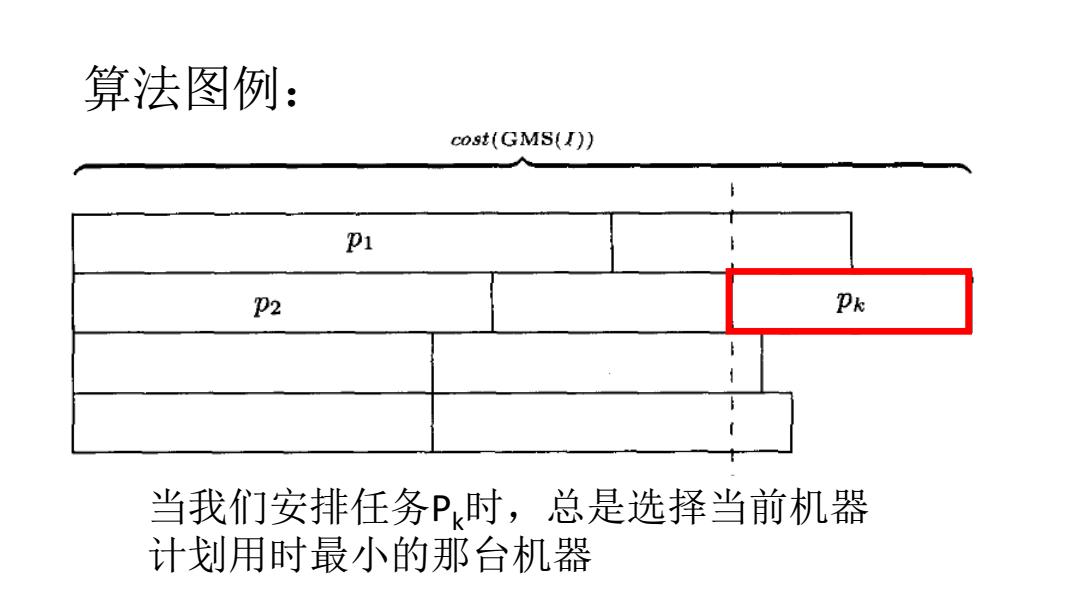
算法图例: cost(GMS(I)) P1 P2 Pk 当我们安排任务P时,总是选择当前机器 计划用时最小的那台机器
算法图例: 当我们安排任务Pk时,总是选择当前机器 计划用时最小的那台机器

生产调度问题的一个近似解 Algorithm 4.2.1.3 (GMS (GREEDY MAKESPAN SCHEDULE)). Input:I=(p1,...,pn,m),n,m,p1,...,p ositive integers and m 2. Step 1:Sort p1,...,Pn. To simplify the nota 2p2≥T≥pn in the rest of th hm. Step 2: for i 这个算法会 差到什么程 edistributed to the 度呢? dices of all jobs ,m.} 40 b compce an I such that me(T):=min{Time(T,)1≤j≤m}; T:=TU{}: Time(T):=Time(Ti)+pi end Output:(T,T2,.,Tm)为
生产调度问题的一个近似解 这个算法会 差到什么程 度呢?
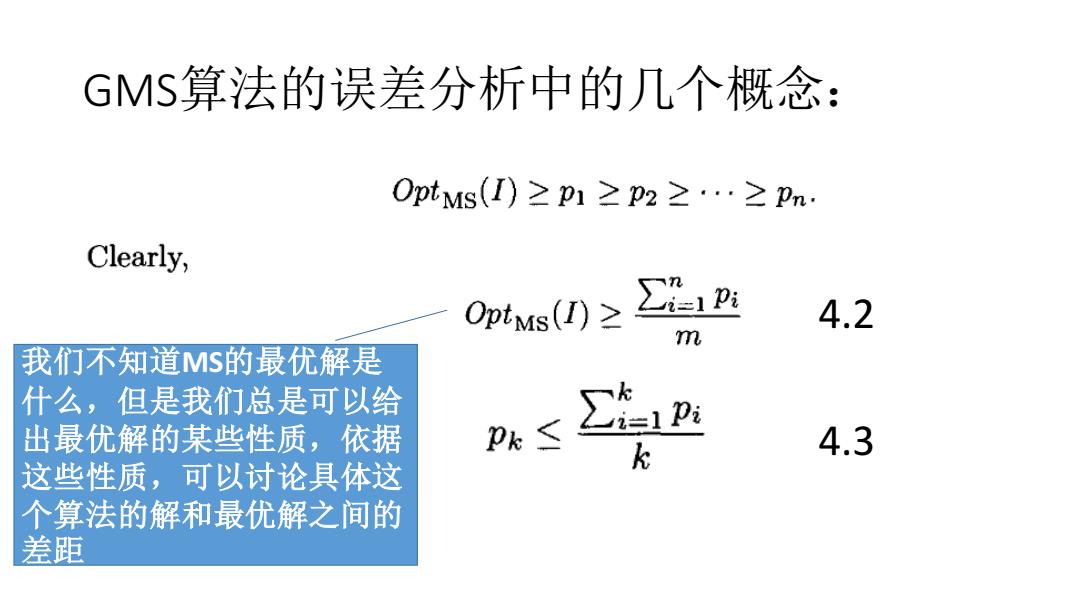
GMS算法的误差分析中的几个概念: 0ptMs(I)≥p1≥p2≥·≥pn: Clearly, OptMs(I)≥ ∑21p 4.2 m 我们不知道MS的最优解是 什么,但是我们总是可以给 出最优解的某些性质,依据 Pk≤ k 4.3 这些性质,可以讨论具体这 个算法的解和最优解之间的 差距
GMS算法的误差分析中的几个概念: 4.2 我们不知道MS的最优解是 什么,但是我们总是可以给 出最优解的某些性质,依据 这些性质,可以讨论具体这 个算法的解和最优解之间的 差距 4.3

证明概要(只讨论任务数大于机器数): Let n>m. Let Ti be such that cost(Ti)=rTP=cost(GMS()),and let k be the largest index in Ti.If k m,then T=1 and so Optms(1)=p1 pk and GMS(D)is an optimal solution. Now,assume m <k.Following Figure 4.2 we see that 什么是T? 这里有完整证明中的第二层分情形证明,是什么?
证明概要(只讨论任务数大于机器数): 什么是Tl? 这里有完整证明中的第二层分情形证明,是什么?
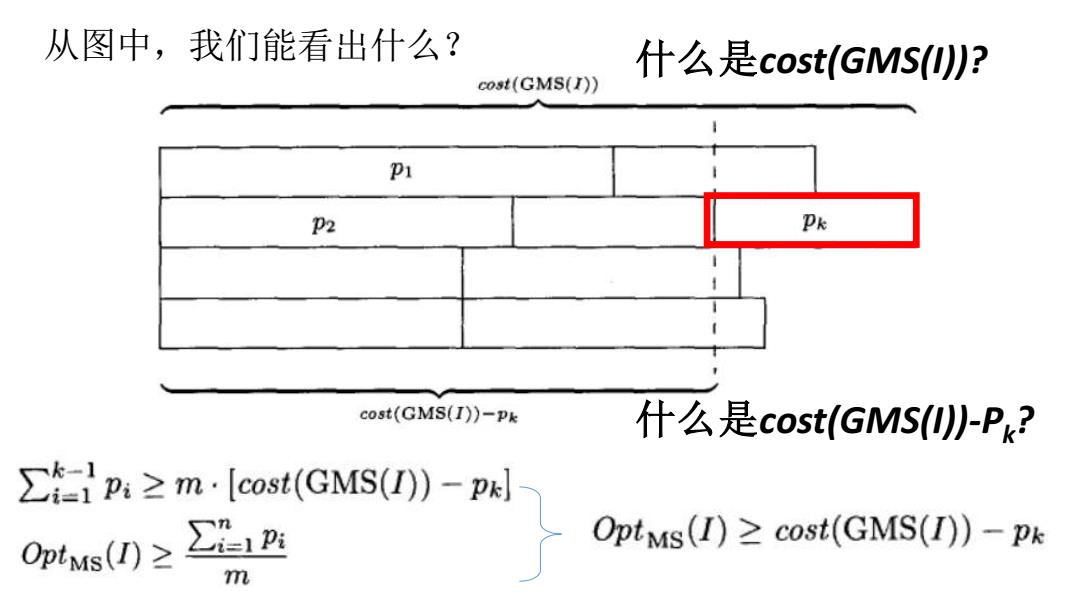
从图中,我们能看出什么? 什么是cost(GMSI)? cost(GMS(I)) P1 P2 Pk cost(GMS(I))-Pk 什么是cost(GMSI-Pk? ∑ipn:≥m·[cost(GMS(I)-pkl OptMs(I)≥ ∑2 OptMs(I)>cost(GMS(I))-pk m
从图中,我们能看出什么? 什么是cost(GMS(I))? 什么是cost(GMS(I))-Pk?