
我们希望能够得到某个近似算法的如下结论: For any positive real 6 1,we say that A is a 6-approximation algo- rithm for U if RA(z)≤6 for every x∈Lr: 如果不能,我们要努力得到某个近似算法的这个结论: For every function f:NN-R,we say that A is an f(n)-approximation algorithm for U if RA(n)≤f(n)for every n∈N
我们希望能够得到某个近似算法的如下结论: 如果不能,我们要努力得到某个近似算法的这个结论:

如何评价一个近似算法的“好坏” 1,针对某个特定的问题输入,A的解和最优解的误差 在不知道最优解的情况下,如何评估? 2,针对某个规模的各种问题输入,A的最大误差; 3,针对问题的所有可能输入,A的误差变化趋势: 将所有输入可能,建模为n的增长 4,给出一个误差的界限,证明A近似算法的误差的界限 绝对的某个值,或者某个函数
如何评价一个近似算法的“好坏” 1,针对某个特定的问题输入,A的解和最优解的误差 在不知道最优解的情况下,如何评估? 2,针对某个规模的各种问题输入,A的最大误差; 3,针对问题的所有可能输入,A的误差变化趋势: 将所有输入可能,建模为n的增长 4,给出一个误差的界限,证明A近似算法的误差的界限 绝对的某个值,或者某个函数
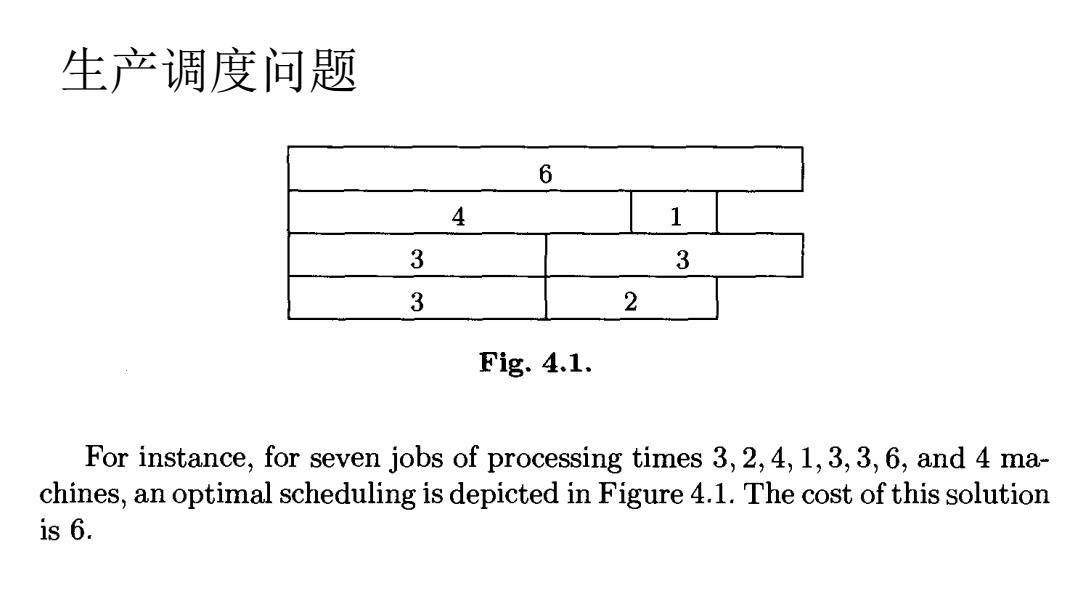
生产调度问题 6 4 1 3 3 3 2 Fig.4.1. For instance,for seven jobs of processing times 3,2,4,1,3,3,6,and 4 ma- chines,an optimal scheduling is depicted in Figure 4.1.The cost of this solution s6
生产调度问题

生产调度问题的一个近似解 Algorithm 4.2.1.3 (GMS (GREEDY MAKESPAN SCHEDULE)). Input:I=(p1,...,Pn,m),n,m,p1,...,Pn positive integers and m 2. Step 1:Sort p1,...,Pn. To simplify the notation we assume p1≥p2≥·≥pn in the rest of the algorithm. Step 2:for i=1 to m do begin Ta:={i); Time(Ti):=pi end In the initialization step the m largest jobs are distributed to the m machines.At the end,Ti should contain the indices of all jobs assigned to the ith machine for i=1,...,m.} Step 3:for i=m+1 to n do begin compute an I such that Time(T)=min{Time(Til≤j≤m; T:=TUfi: Time(Ti):=Time(Ti)+pi end Output:(Ti,T2,...,Tm)
生产调度问题的一个近似解
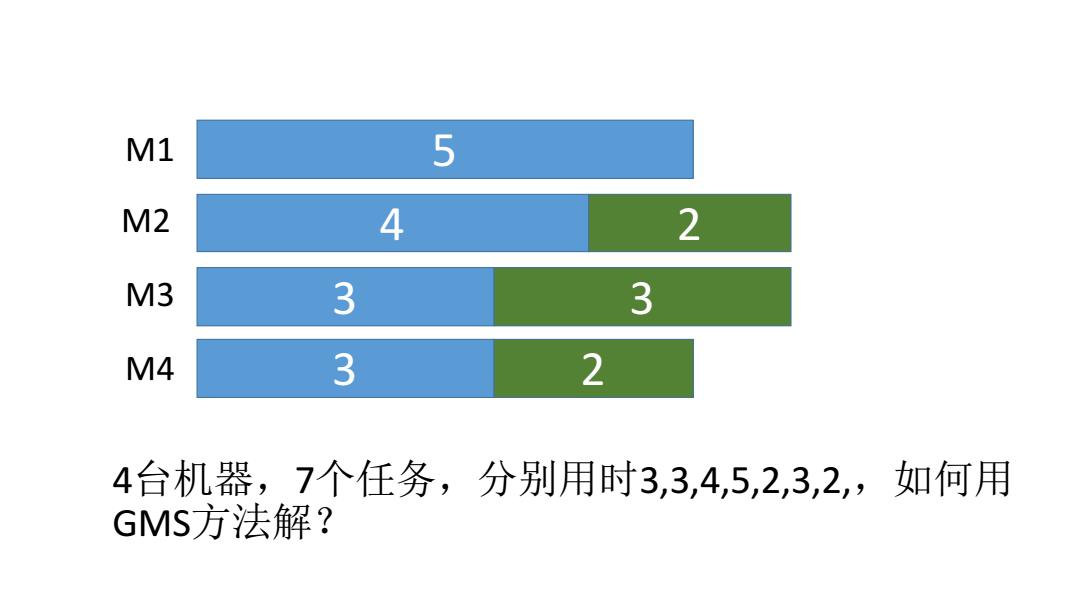
M1 5 M2 4 2 M3 3 3 M4 3 2 4台机器,7个任务,分别用时3,3,4,5,2,3,2,如何用 GMS方法解?
4台机器,7个任务,分别用时3,3,4,5,2,3,2,,如何用 GMS方法解? M1 M2 M3 M4 5 4 3 3 3 2 2