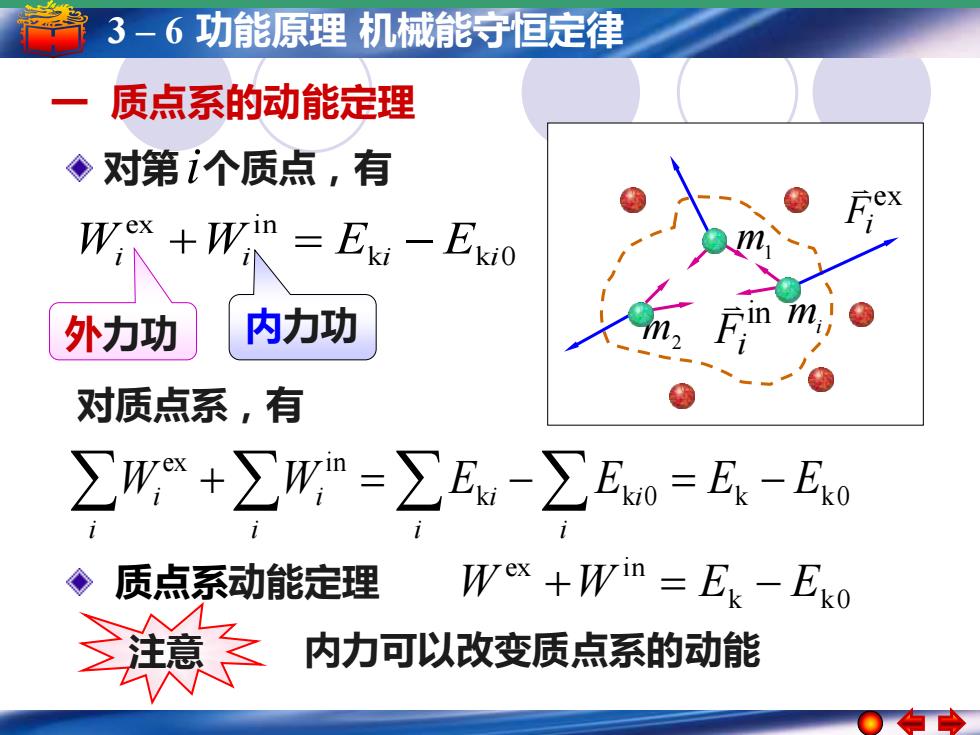
3-6功能原理机械能守恒定律 质点系的动能定理 ◆对第个质点,有 Wex +Wrin =Ek-Ekio 外力功 内力功 对质点系,有 ∑W+∑=∑E-∑Ew=E-Ew ◆质点系动能定理 Wex +win =Ek-Eko 柔 内力可以改变质点系的动能
5 3 ––16简谐运动 功能原理简谐运动的振幅 机械能守恒定律 周期 频率和相位 一 质点系的动能定理 质点系动能定理 k k0 ex i n W +W = E − E m1 m2 mi ex Fi in Fi 注意 内力可以改变质点系的动能 k k 0 k k0 ex i n W W E E E E i i i i i i i i + = − = − 对质点系,有 k k 0 ex i n Wi +Wi = E i − E i 对第 i 个质点,有 外力功 内力功

3-6功能原理机械能守恒定律 二质点系的功能原理 质点系动能定理 wex+win =Ek-Es Wn=∑Wn=Wg+W8 非保守 力的功 W"=-(∑E-∑Eo)=-(E,-Eo) Wx+W=(E+E)-(Eko+E0) 机械能E=Ek+E, Wex +Wne =E-Eo 质点系的功能原理:质点系机械能的增量等于 外力和非保守内力作功之和
5 3 ––16简谐运动 功能原理简谐运动的振幅 机械能守恒定律 周期 频率和相位 ( ) ( ) k p k0 p0 i n nc ex W +W = E + E − E + E 机械能 E = Ek + Ep 质点系动能定理 k k0 ex i n W +W = E − E 非保守 力的功 i n nc i n c i n i n W W W W i = i = + ( ) ( ) p p 0 p p0 in Wc E E E E i i i = − i − = − − 0 i n nc ex W +W = E − E 二 质点系的功能原理 质点系的功能原理:质点系机械能的增量等于 外力和非保守内力作功之和

3-6功能原理机械能守恒定律 三 机械能守恒定律 功能原理Wx+WC=(E+E,)-(Ek0+E0) 当Wex+Wn=0 nc 时,有E=E。 机械能守恒定律:只有保守内力作功的情况下,质 点系的机械能保持不变· Ek-Ek0=-(E。-E0) △Ek=-△E。 守恒定律的意义 不究过程细节而能对系统的状态下结论,这是各 个守恒定律的特点和优点
5 3 ––16简谐运动 功能原理简谐运动的振幅 机械能守恒定律 周期 频率和相位 Ek = −Ep ( ) Ek − Ek0 = − Ep − Ep0 当 0 in nc ex W +W = 时,有 E = E0 ( ) ( ) k p k0 p0 i n nc ex 功能原理 W +W = E + E − E + E 三 机械能守恒定律 机械能守恒定律:只有保守内力作功的情况下,质 点系的机械能保持不变 . 守恒定律的意义 不究过程细节而能对系统的状态下结论,这是各 个守恒定律的特点和优点

3-6功能原理机械能守恒定律 讨论 如图所示的系统,物体A、B置于光滑的桌面上, 物体A和C,B和D之间摩擦因数均不为零,首先用 外力沿水平方向相向推压A和B,使弹簧压缩,后拆 除外力,则A和B弹开过程中,对A、B、C、D组成 的系统 (A)动量守恒,机械能守恒 (B)动量不守恒,机械能守恒 (C)动量不守恒,机械能不守恒 (D)动量守恒,机械能不一定守恒 D M B WWWWM B
5 3 ––16简谐运动 功能原理简谐运动的振幅 机械能守恒定律 周期 频率和相位 如图所示的系统, 物体 A、B 置于光滑的桌面上, 物体 A 和 C, B和 D 之间摩擦因数均不为零, 首先用 外力沿水平方向相向推压 A 和 B,使弹簧压缩,后拆 除外力,则 A 和 B 弹开过程中,对 A、B、C、D 组成 的系统 讨论 (A)动量守恒,机械能守恒 (B)动量不守恒,机械能守恒 (C)动量不守恒,机械能不守恒 (D)动量守恒,机械能不一定守恒 D B C A D B C A

3-6功能原理机械能守恒定律 讨论 下列各物理量中,与参照系有关的物 理量是哪些? (不考虑相对论效应) (1)质量 (2)动量 (3)冲量 (4)动能 (5)势能 (6) 功 答:动量、动能、功
5 3 ––16简谐运动 功能原理简谐运动的振幅 机械能守恒定律 周期 频率和相位 下列各物理量中,与参照系有关的物 理量是哪些? (不考虑相对论效应) (1)质量 (2) 动量 (3) 冲量 (4) 动能 (5) 势能 (6) 功 答:动量、动能、功 . 讨 论