
Recitation:Radiation Exchange between Surfaces ·The view factor Radiosity J Emissive Power (E) Reflective Power(Grer) Radiosity.J qi→j Incident Radiation AJ G FA=AF A fraction of the total seen by Aj
Recitation: Radiation Exchange between Surfaces • The view factor Radiosity , i j i j i i q F A J i J Emissive Power (E) Reflective Power (Gref) Fi, j Ai AjFj,i A fraction of the total seen by Aj ρG E G

Blackbody Radiation Exchange qi=FiAJ q=FiAJ If A &A are blackbody,no reflection, J=E。=oT4 Net radiation heat transfer between the surfaces △q=FA,oI-FA,oI, △9=FA,(T4-T)
• Blackbody Radiation Exchange i j i j i i q F A J , 4 J Eb T j i j i j j q F A J , If Ai &Aj are blackbody, no reflection, Net radiation heat transfer between the surfaces 4 , 4 ij Fi, j Ai Ti Fj iAj Tj q ( ) 4 4 ij Fi, j Ai Ti Tj q
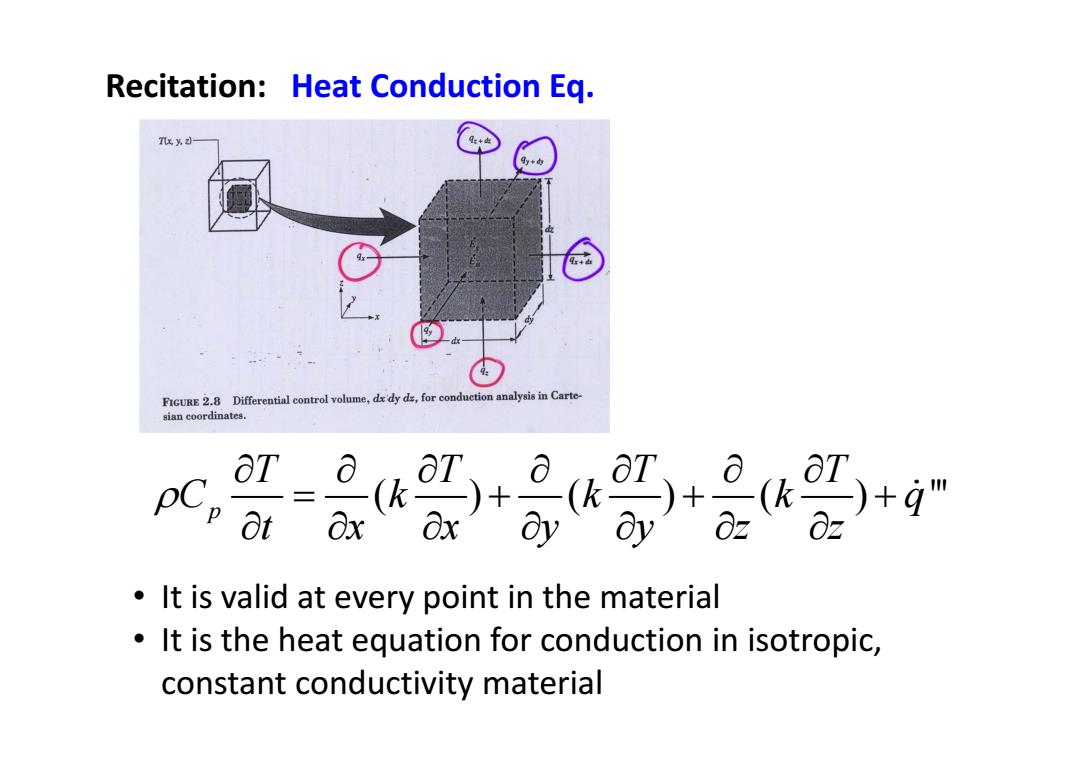
Recitation:Heat Conduction Eq. 比%小 FIGURE 2.8 Differential control volume,dx dy ds,for conduction analysis in Carte- sian coordinates 二 -(k)g It is valid at every point in the material It is the heat equation for conduction in isotropic, constant conductivity material
( ) ( ) ( ) ''' p TT T T C k k kq txx yy zz • It is valid at every point in the material • It is the heat equation for conduction in isotropic, constant conductivity material Recitation: Heat Conduction Eq

In Cylindrical coordinate systems: ++k+”=c at Y k a2T o2t aT In spherical coordinate systems: k 02T k∂ ot r2 Or sin0 0+r2sing 00 (sing +9 t pCp at
In Cylindrical coordinate systems: In spherical coordinate systems:

Boundary Conditions and Initial Conditions insulation Tlx=0 To 0 0 convection,h,T ot 一k =0 ay y=W OT -k·y=0=h7m-T(x,0]
Boundary Conditions and Initial Conditions