
互補原則(Bohr's Principle of Complementary) Bohr's Principle of Complementary The particle and the wave models are complementary No measurements can simultaneously reveal the particle and the wave properties of matter. 再重複一下重點 ·de Broglie Hypothesis:粒子的行為應該以一個物質波函數(matter wave)平(r,t)來形容,這個波函數可以提供有關粒子位置及動量的訊息 形容粒子行為的物質波函數為一機率波The probability that the particle will be found in volume dV: P(r,t)dV=I平|2dV,P(r,t)=Y2:probability density機率密度
互補原則 ( Bohr’s Principle of Complementary ) Bohr’s Principle of Complementary : The particle and the wave models are complementary • No measurements can simultaneously reveal the particle and the wave properties of matter. 再重複一下重點 • de Broglie Hypothesis : 粒子的行為應該以一個物質波函數 ( matter wave ) Y( r,t ) 來形容 , 這個波函數可以提供有關粒子位置及動量的訊息 • 形容粒子行為的物質波函數為一機率波 The probability that the particle will be found in volume dV : P( r,t ) dV = Y 2 dV , P( r,t ) = Y 2 : probability density 機率密度

·例如:一個在一維空間中以等速率運動的粒子: 其波函數可以Y(x,t)=Asin(kx-ot),k=2π入,o=2πD代表 →this particle: (1)has a well-defined p=h/ (2)P(x,t dx=2dx A2dx at any point Particle can be found with equal probability at any point (因為粒子以等速率自∞移動至+∞處,因此在各點出現及停留的 時間都一樣) 這是最簡單的一個物理系統(以等速度運動的單一粒子),其他的物理系 統都比這個複雜的多(沒有固定的速度及動量,粒子在各點出現的機率也 不同) →波函數的形式複雜許多,沒有固定的波長或固定的振幅 (求速度(或動量)的平均值及粒子出現位置的平均值有時可能比較重要)
• 例如 : 一個在一維空間中以等速率運動的粒子 : 其波函數可以 Y( x,t ) = A sin( kx – wt ) , k = 2p/l , w = 2p u 代表 this particle : (1) has a well-defined p= h/l (2) P( x,t ) dx = Y 2 dx = A2dx at any point Particle can be found with equal probability at any point ( 因為粒子以等速率自– 移動至 + 處 , 因此在各點出現及停留的 時間都一樣 ) 這是最簡單的一個物理系統 ( 以等速度運動的單一粒子 ) ,其他的物理系 統都比這個複雜的多 ( 沒有固定的速度及動量,粒子在各點出現的機率也 不同 ) 波函數的形式複雜許多,沒有固定的波長或固定的振幅 ( 求速度 ( 或動量 ) 的平均值及粒子出現位置的平均值有時可能比較重要 )
魏察者 粒子最可能 出现的位置 KA-BooM! 量子力学就 量子力學的處理方法
量子力學的處理方法
薛丁格理論(The Schrodinger Theory) ·平不同於“物理波”,所以不必一定要是實數,也可以是複數形式, 也就是說可以同時包含實數項及虚數項的波函數 ·如何在平面座標上表示出一個複數? 虛數軸 Ae+i0= etio=cos0±i sine A(cose+isine Euler's identity (Asine) Aeie=A(cos0±isin0) 實數軸 complex conjugate (A cose) Aeti )*Ae-i (Aeti )*=Ae-i= 複數平面 A(cose-i sine) .Ae+i(kx-ot )=A cos(kx-ot )+isin(kx ot ) free particle wave function,Y(x,t
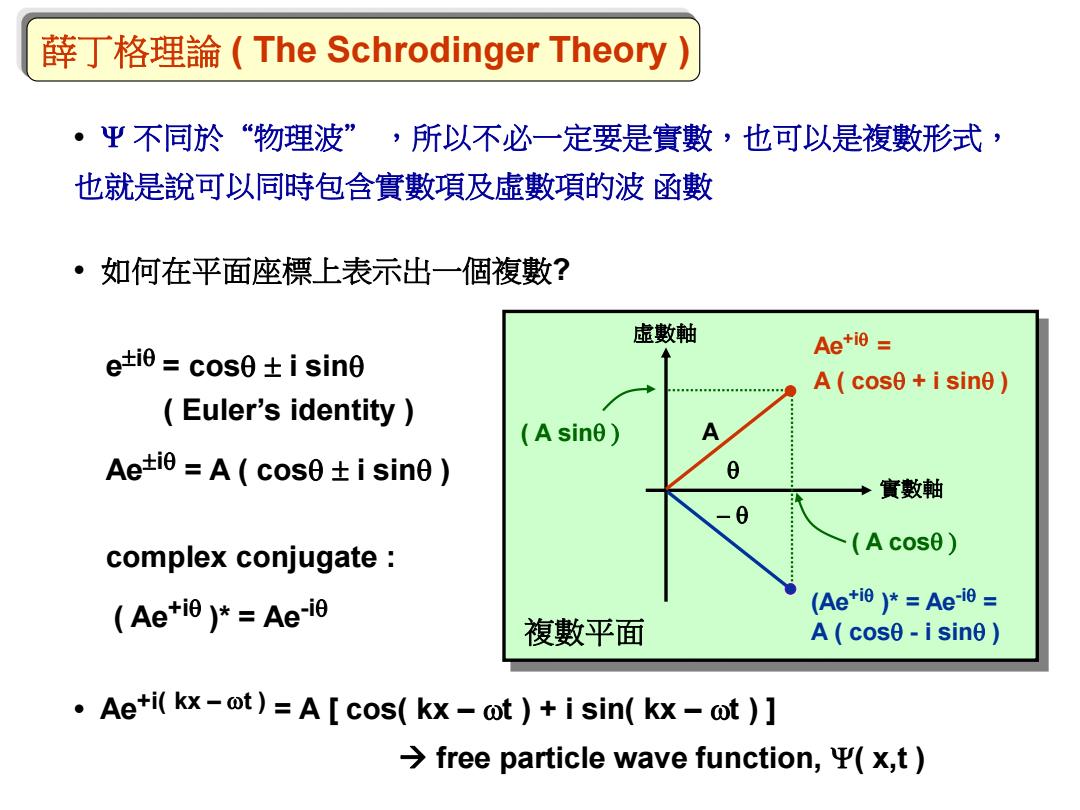
薛丁格理論 ( The Schrodinger Theory ) • Y 不同於“物理波” ,所以不必一定要是實數,也可以是複數形式, 也就是說可以同時包含實數項及虛數項的波 函數 • 如何在平面座標上表示出一個複數? e iq = cosq i sinq ( Euler’s identity ) Ae iq = A ( cosq i sinq ) complex conjugate : ( Ae +iq )* = Ae -iq • Ae +i( kx – wt ) = A [ cos( kx – wt ) + i sin( kx – wt ) ] free particle wave function, Y( x,t ) q - q A Ae +iq = A ( cosq + i sinq ) ( A cosq ) (Ae +iq )* = Ae -iq = A ( cosq - i sinq ) ( A sinq ) 複數平面 實數軸 虛數軸

例如:Aeti(kx-mt)=A[cos(kx-ot)+isin(kx-t)] free particle wave function,Y(x,t (平不同於“物理波”,不必一定要是實數) |平|=A,平2=A2→所有位置出現機率相同 此複數形式波函數有“實數波”及“虛數波”兩個部分,此雨部份均 具有明確及相同的波長及頻率: 「入=2π/k (0=0/2元 因此所描述的粒子應該具有確定的動量及能量: p=hIλ E=hv ·對此複數形式波函數,還有另一個求算其所描述之粒子的動量及能量 的方法
例如 : Ae +i( kx – wt ) = A [ cos( kx – wt ) + i sin( kx – wt ) ] free particle wave function, Y( x,t ) ( Y 不同於“物理波”, 不必一定要是實數 ) Y = A , Y 2 = A2 所有位置出現機率相同 此複數形式波函數有“實數波”及“虛數波”兩個部分 , 此兩部份均 具有明確及相同的波長及頻率 : l = 2p / k u = w / 2p 因此所描述的粒子應該具有確定的動量及能量 : p = h / l E = hu • 對此複數形式波函數 , 還有另一個求算其所描述之粒子的動量及能量 的方法