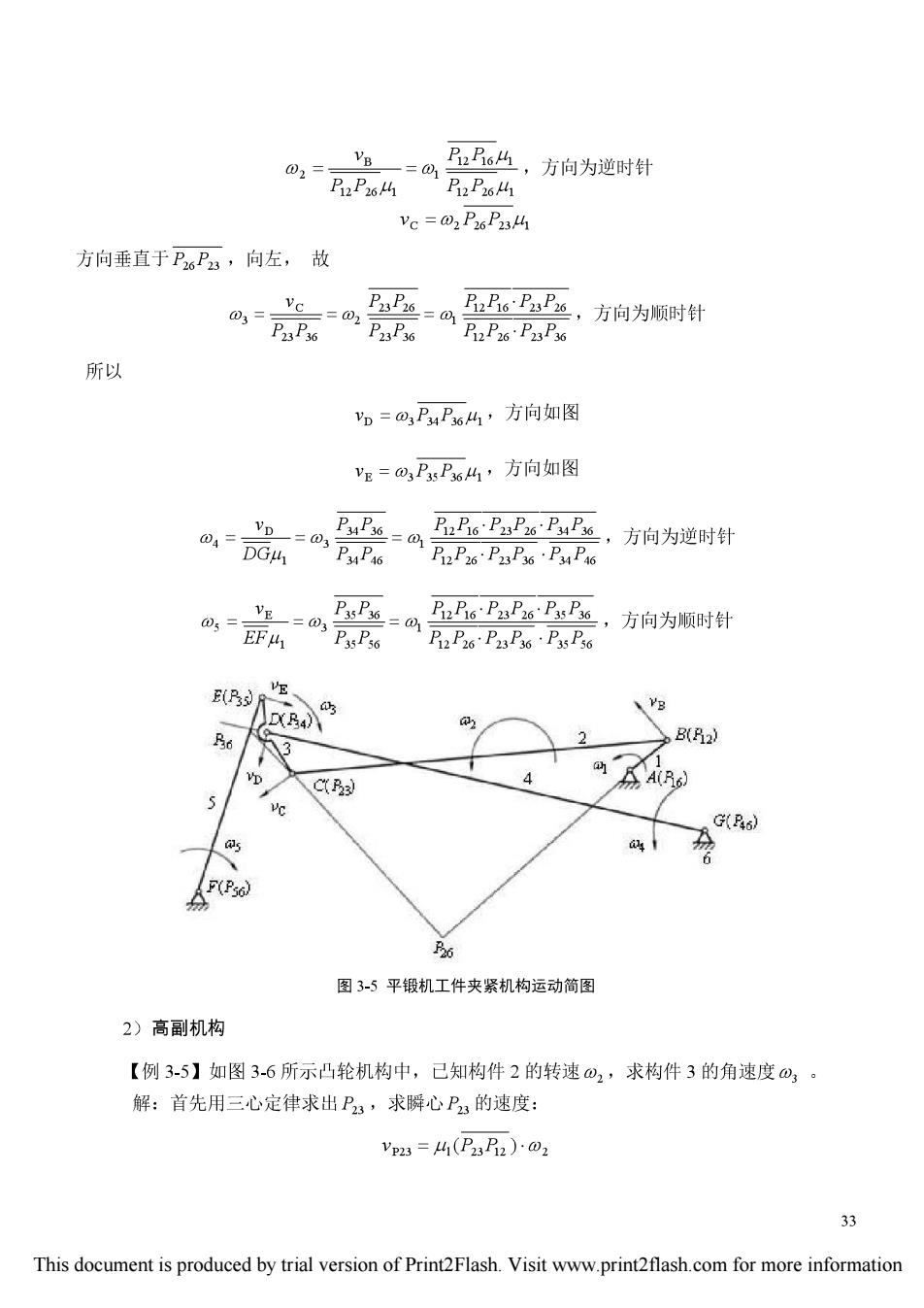
02 VB B丛,方向为逆时针 2P2641 B2P2641 Vc=02P6P234 方向垂直于P6P,向左,故 03= =@ P23P36 6P6,方向为顺时针 P23P36 2P26·P23P36 所以 p=@P4P641’方向如图 E=3P35P3641,方向如图 04= P46=0 B6PP6~乃P6,方向为逆时针 DGu P34P46 乃2P26·P23P36·P34P6 PxsPx6= VE-03 PysPs6 BB6PP6PP6,方向为顺时针 EF B2P6P23P6·P35Ps6 E(P3R D(B4八 6 B(32》 凡3 饰 C《(B 4 AA(6】 e G(Rs) 5 6 ho Bo 图3-5平锻机工件夹紧机构运动简图 2)高副机构 【例3-5】如图3-6所示凸轮机构中,已知构件2的转速⊙2,求构件3的角速度@3。 解:首先用三心定律求出P3,求瞬心P3的速度: Vp23=4(P232)02 33 This document is produced by trial version of Print2Flash.Visit www.print2flash.com for more information
This document is produced by trial version of Print2Flash. Visit www.print2flash.com for more information

Vp23=41(P233)·03 所以 ①3=①2·(P33/P3R3),方向与02相反。 【例3-6】如图3-7所示为一直动从动件凸轮机构。设已知各构件的尺寸和原动件1的角速 度,求从动件2的速度v2。 解:因为构件2作平动,所以利用瞬心乃2是构件1和2的等速重合点,即可求得y2。 由于构件1、2组成高副,所以瞬心P2在过接触点K处的公法线n-n上;又由三心定理知, 瞬心乃2与R3、P3共线。因此过R3作P3的方向线与n-n线的交点即为瞬心R2。 V2=Vp业=a0乃2341 2方向向上,如图3-7所示。 3→9 3 2 2 B3→0 图3-6图解法求高副机构的角速度 图3-7直动从动件凸轮机构 利用速度瞬心法对简单机构的速度分析非常简便。但对于包含构件数目较多的机构,由于瞬 心数目较多,使得求解困难。需要特别说明的是,速度瞬心法仅限于对机构的速度分析,不便用 于加速度分析。 3.3用相对运动图解法对机构进行运动分析 相对运动图解法(relative kinematic graphic method)也称为矢量方程图解法(vector graphic method),所依据的是理论力学中的运动合成原理。在对机构进行速度、加速度分析时,根据运 动合成原理列出速度、加速度运动矢量方程,按矢量运算作图求解。下面就在机构运动分析中所 遇到的两种不同情况对其基本原理和方法加以说明。 3.3.1作平面运动的同一构件上两点间的运动分析 如图3-8所示为铰链四杆机构运动简图。已知各构件的尺寸及原动件1以等角速度),逆时 针方向转动,求机构在图示位置时构件2、3的角速度o2、o3和角加速度x2、:,以及构件2 34 This document is produced by trial version of Print2Flash.Visit www.print2flash.com for more information
This document is produced by trial version of Print2Flash. Visit www.print2flash.com for more information

上点E的速度vE和加速度xe。 用相对运动图解法进行运动分析时,应沿着机构的运动传递顺序,从与运动已知的原动件相 连的杆组开始,以杆组为单位依次进行。首先确定杆组中外接副的运动(往往是己知的),其次 确定杆组内接副的运动,然后再确定构件上一般点的运动。 B 4 (a) 铰链四杆机构运动简图 (b)速度多边形 (c)加速度多边形 图3-8同一构件上两点之间的运动图解分析 1.列出运动矢量方程式 铰链四杆机构仅含有一个Ⅱ级杆组BCD,且外接副点B、D的运动已知,所以先求内接副 点C的运动。而点C和B同在连杆2上,选运动己知的点B为基点,由运动合成原理,点C的 运动可视为随着基点B作平动与绕着基点B作相对转动的合成。所以点C的速度v。和加速度ac 的矢量方程分别表示为 Vc VB VCB (3-2) 方向: ⊥CD⊥AB ⊥BC 大小: n @LAB (3-3) 方向: C→D⊥CD B→AC→B⊥BC 大小: @jlcD ? 021AB @2lBc 式中,yc、a8、a为点C相对于点B的相对速度、相对法向加速度和相对切向加速度; a心、a心分别为点C的绝对法向加速度和切向加速度。 为了减少方程中未知量的数目,将转动加速度分解为法向和切向两个分量,每一项的大小 和方向均示于式中。在式(3-2)中,仅vc、vc的大小未知,而在式(3-3)中,经过速度分析 之后a也为已知,仅有a心、a的大小未知,故每个方程组仅包含两个未知量,可以用作图 法求解。 35 This document is produced by trial version of Print2Flash.Visit www.print2flash.com for more information
This document is produced by trial version of Print2Flash. Visit www.print2flash.com for more information