下传动级数要尽量地少。 大功率减速传动装置按“质量最小原则”确定的各级传动表现为“前大后小”的传动比分 配方式。减速齿轮传动的后级齿轮比前级齿轮的转矩要大得多,同样传动比的情祝下齿厚、质量 也大得多,因此减小后级传动比就相应减少了大齿轮的齿数和质量。 大功率诚速传动装置的各级传动此可以按图2-7和图28选择。 10 200300 00 图27大功率传动装置两级传动比曲线 图2.8大功率传动装置三级传动比曲线 (1<10时,使用图中的虚线 (i<100时,使用图中的虚线) 例2-3:设n=2,i=40,求各级传动此。 解 查图2-7可得i1≈9.1:2≈4.4 例2-4:设n=3,i=22,求各级传动此。 解: 查图28可得i1≈12:b≈5:i3≈3.4 (2)小功率传动装置 对于小功率传动装置,按“质量最小”原则来确定传 动此时,通常选择相等的各级传动此。在假设各主动小齿 轮的模数、齿数均相等这样的特殊条件下,各大齿轮的分 度圆直径均相等,因而每级齿轮副的中心距也相等。这样 便可设计成如图2-9所示的回曲式齿轮传动链:其总 图2-9回曲式齿轮传动链 传动比可以非常大。显然,这种结构十分紧凑 3、输出轴转角误差最小原划 以图2-10所示四级齿轮减速传动链为例。四级传动比分别为、。、、4,齿轮上8的转 角误差依次为△心,一△Dg。该传动链输出轴的总转动角误差△中为: △+△,+A+A,+A+A9+A1+A A中m=iig4 (2-7) 24 由上式可以看出,如果从输入端到输出端的各级传动比按“前小后大”原则排列,则总转角 误差较小。而且低速级的误差在总误差中占的比重很大。因此,要提高传动精度,就应减少传动 级数。并使末级齿轮的传动此尽可能大,制造精度尽量高。 4、三种原则的选择 在设计齿轮传动装置时,上述三条原则应根据具体工作条件综合考虑。 6
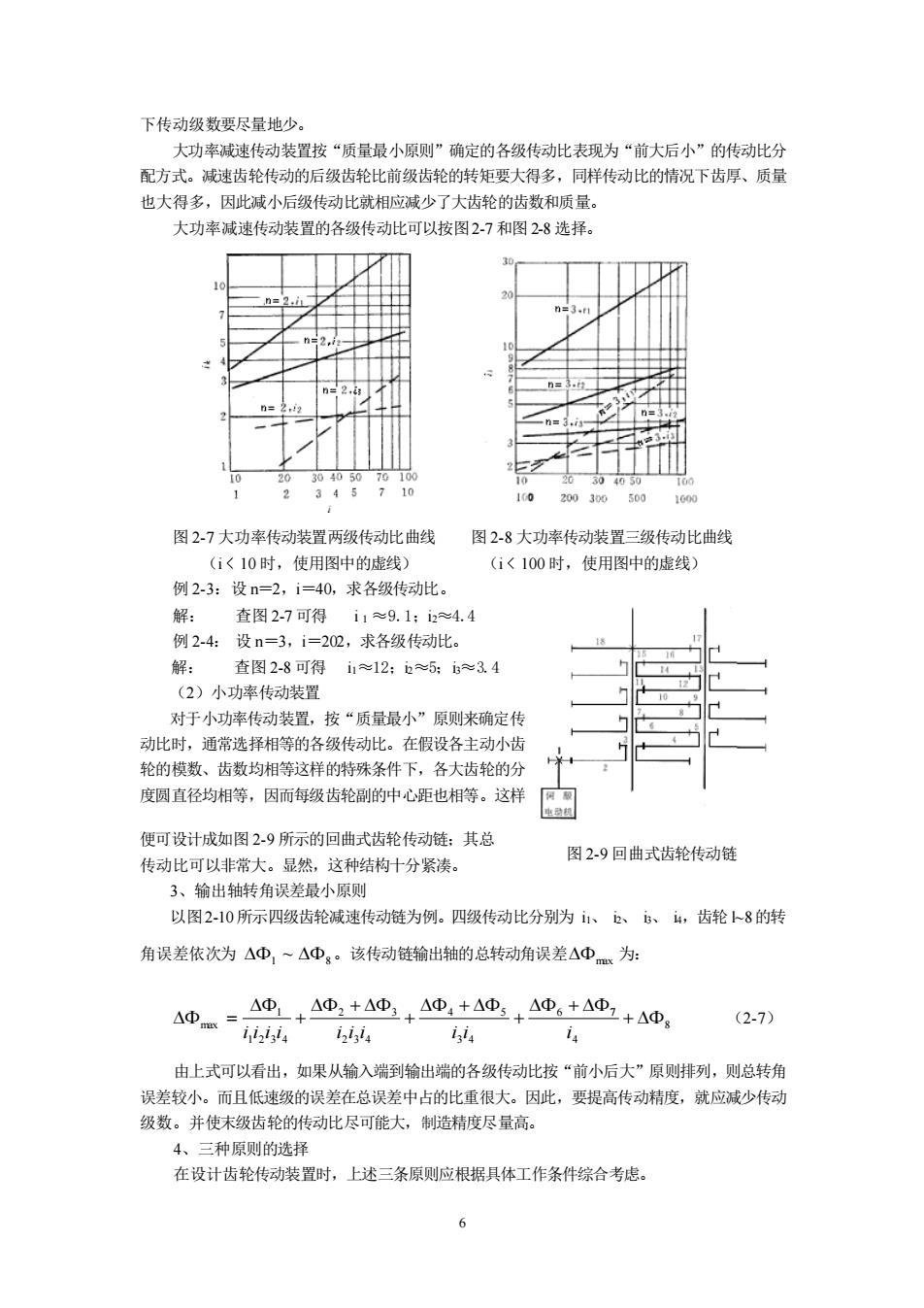
6 下传动级数要尽量地少。 大功率减速传动装置按“质量最小原则”确定的各级传动比表现为“前大后小”的传动比分 配方式。减速齿轮传动的后级齿轮比前级齿轮的转矩要大得多,同样传动比的情况下齿厚、质量 也大得多,因此减小后级传动比就相应减少了大齿轮的齿数和质量。 大功率减速传动装置的各级传动比可以按图2-7 和图 2-8 选择。 图 2-7 大功率传动装置两级传动比曲线 图 2-8 大功率传动装置三级传动比曲线 (i < 10 时,使用图中的虚线) (i < 100 时,使用图中的虚线) 例 2-3:设 n=2,i=40,求各级传动比。 解: 查图 2-7 可得 i 1 ≈9.1;i2≈4.4 例 2-4: 设 n=3,i=202,求各级传动比。 解: 查图 2-8 可得 i1≈12;i2≈5;i3≈3.4 (2)小功率传动装置 对于小功率传动装置,按“质量最小”原则来确定传 动比时,通常选择相等的各级传动比。在假设各主动小齿 轮的模数、齿数均相等这样的特殊条件下,各大齿轮的分 度圆直径均相等,因而每级齿轮副的中心距也相等。这样 便可设计成如图 2-9 所示的回曲式齿轮传动链;其总 传动比可以非常大。显然,这种结构十分紧凑。 3、输出轴转角误差最小原则 以图2-10所示四级齿轮减速传动链为例。四级传动比分别为 i1、 i2、 i3、 i4,齿轮 l~8的转 角误差依次为 1 ~ 8 。该传动链输出轴的总转动角误差 max 为: 8 4 6 7 3 4 4 5 2 3 4 2 3 1 2 3 4 1 max + + + + + + + = i i i i i i i i i i (2-7) 由上式可以看出,如果从输入端到输出端的各级传动比按“前小后大”原则排列,则总转角 误差较小。而且低速级的误差在总误差中占的比重很大。因此,要提高传动精度,就应减少传动 级数。并使末级齿轮的传动比尽可能大,制造精度尽量高。 4、三种原则的选择 在设计齿轮传动装置时,上述三条原则应根据具体工作条件综合考虑。 图 2-9 回曲式齿轮传动链
(1)对于传动精度要求高的降速齿轮传动链,可按输出轴转角误差最小的原则设计。若为 增速传动,则应在开始几级就增速 (2)对于要求运转平稳、启停须繁和动 给出 态性能好的降速传动链,可按等效转动惯量 最小原则和输出轴转角误差最小的原则设 计。 (3)对于要求质量尽可能小的降速传 动链,可按质量最小原则设计。 图2-10四级减速齿轮传动链 第三节机械系统性能分析 为了保证机电一体化系统具有良好的同服特性,我们不仅要满足系统的静态特性,还必须利 用自动控制理论的方法进行机电一体化系统的动态分析与设计。动态设计过程首先是针对静态设 十的系统建立数学模型,然后用控制理论的方法分析系统的频率特性, 找出并通过调节相关机械 参数改变系统的伺服性能。 一、数学棋型建立 机械系统的数学模型建立与电气系统数学模型建立基本相似,都是通过折算的办法将复杂的 结构装置转换成等效的简单函授关系,数学表达式一般是线性微分方程(通常简化成二阶微分方 程)。机械系统的数学模型分析的是输入(如电机转子运动)和输出(如工作台运动)之间的相对 关系。等效折算过程是将复杂结构关系的机械系统的惯量、弹性模量和阻尼(或阻尼比)等机械 性能参数归一处理,从而通过数学模型来反映各环节的机械参数对系统整体的影响。 下面以数控机床进给传动系统为例,来介绍建立数学模型的方法。在图21所示的数控机床 进给传动系统中,电动机通过两级减速齿轮乙、Z、☑、Z乙,及丝杠螺母副驱动工作台作直线运动, 设J为轴1部件和电动机转子构成的转动惯量:Jx、J,为轴Ⅱ、Ⅲ部件构成的转动惯量:K、K K,分别为轴【、Ⅱ、Ⅲ的扭转钢刚度系数:K为丝杠螺母刷及螺母底座部分的轴向钢刚度系数:m为 工作台质量:C为工作台导轨粘性阻尼系数:T、了、分别为轴1、Ⅱ、Ⅲ的输入转矩 图2.11数控机床讲给系线 建立该系统的数学模型,首先是把机械系统中各基本物理量折算到传动链中的某个元件上(本 例折算到轴1上),使复杂的多轴传动关系转化成单一轴运动,转化前后的系统总机械性能等效: 然后,在单一轴基础上根据输入量和输出量的关系建立它的输入输出的学表达式(即数学横 型)。根据该表达式进行的相关机械特性分析就反映了原系统的性能。在该系统的数学模型建立过 7
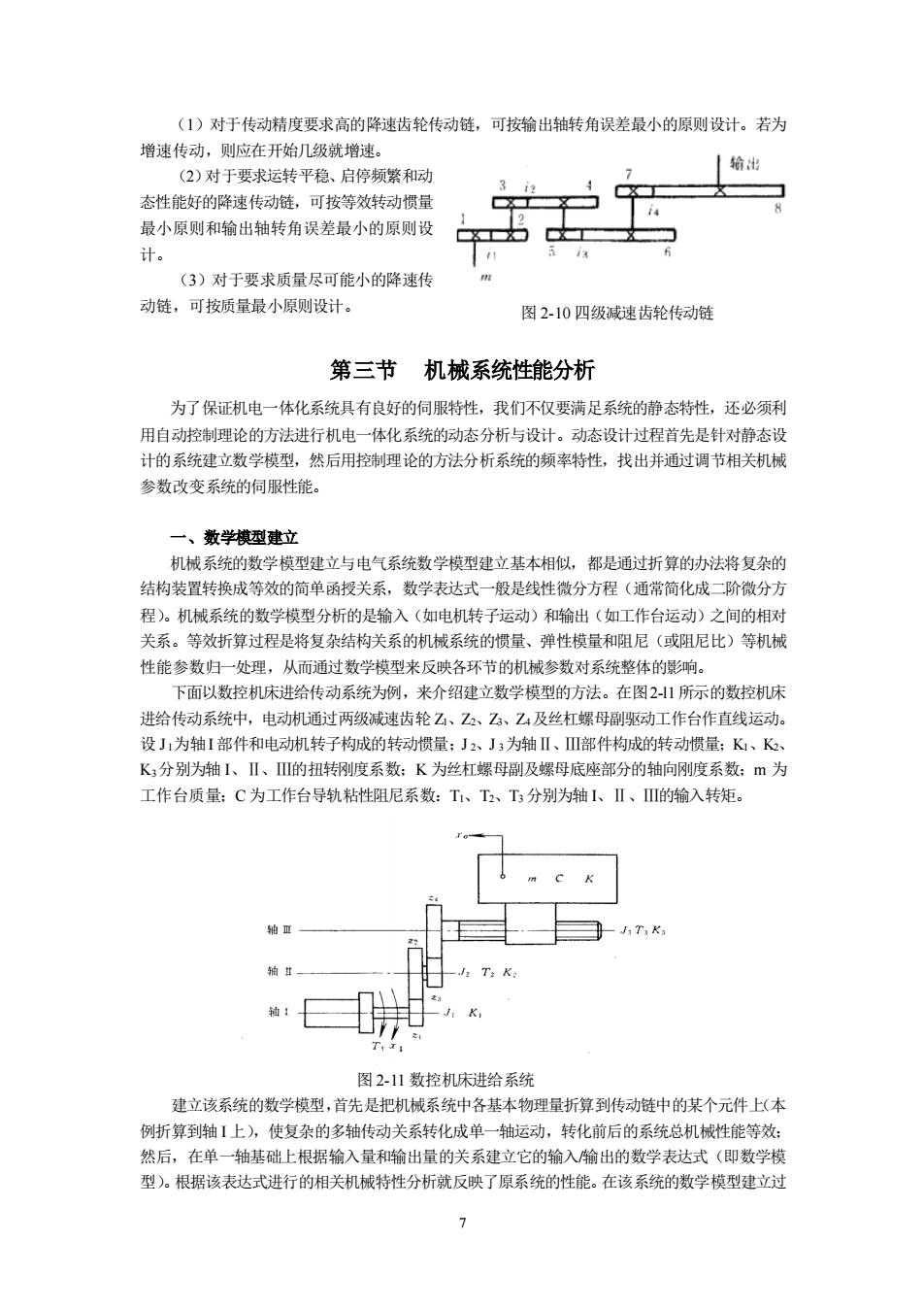
7 (1)对于传动精度要求高的降速齿轮传动链,可按输出轴转角误差最小的原则设计。若为 增速传动,则应在开始几级就增速。 (2)对于要求运转平稳、启停频繁和动 态性能好的降速传动链,可按等效转动惯量 最小原则和输出轴转角误差最小的原则设 计。 (3)对于要求质量尽可能小的降速传 动链,可按质量最小原则设计。 第三节 机械系统性能分析 为了保证机电一体化系统具有良好的伺服特性,我们不仅要满足系统的静态特性,还必须利 用自动控制理论的方法进行机电一体化系统的动态分析与设计。动态设计过程首先是针对静态设 计的系统建立数学模型,然后用控制理论的方法分析系统的频率特性,找出并通过调节相关机械 参数改变系统的伺服性能。 一、数学模型建立 机械系统的数学模型建立与电气系统数学模型建立基本相似,都是通过折算的办法将复杂的 结构装置转换成等效的简单函授关系,数学表达式一般是线性微分方程(通常简化成二阶微分方 程)。机械系统的数学模型分析的是输入(如电机转子运动)和输出(如工作台运动)之间的相对 关系。等效折算过程是将复杂结构关系的机械系统的惯量、弹性模量和阻尼(或阻尼比)等机械 性能参数归一处理,从而通过数学模型来反映各环节的机械参数对系统整体的影响。 下面以数控机床进给传动系统为例,来介绍建立数学模型的方法。在图2-l1所示的数控机床 进给传动系统中,电动机通过两级减速齿轮 Z1、Z2、Z3、Z4及丝杠螺母副驱动工作台作直线运动。 设 Jl为轴I 部件和电动机转子构成的转动惯量;J 2、J 3为轴Ⅱ、Ⅲ部件构成的转动惯量;K1、K2、 K3分别为轴 I、Ⅱ、Ⅲ的扭转刚度系数;K 为丝杠螺母副及螺母底座部分的轴向刚度系数;m 为 工作台质量;C 为工作台导轨粘性阻尼系数:T1、T2、T3 分别为轴 I、Ⅱ、Ⅲ的输入转矩。 图 2-11 数控机床进给系统 建立该系统的数学模型,首先是把机械系统中各基本物理量折算到传动链中的某个元件上(本 例折算到轴 I 上),使复杂的多轴传动关系转化成单一轴运动,转化前后的系统总机械性能等效; 然后,在单一轴基础上根据输入量和输出量的关系建立它的输入/输出的数学表达式(即数学模 型)。根据该表达式进行的相关机械特性分析就反映了原系统的性能。在该系统的数学模型建立过 图 2-10 四级减速齿轮传动链