
两官能团不等当量-Carothers理论(2) J 2x3=1 什5 这样低的平均官能度,表明体系只生成低分子物 ,不会凝胶化 对于两单体官能团不等当量,平均官能度的计算: ©用非过量组分的官能团数的二倍除以体系中的分 子总数
两官能团不等当量--Carothers理论(2)* 这样低的平均官能度,表明体系只生成低分子物 ,不会凝胶化 对于两单体官能团不等当量,平均官能度的计算: 用非过量组分的官能团数的二倍除以体系中的分 子总数

两官能团不等当量-一Carothersi理论(3)* 两种以上单体非等物质量的情况 对于A、B、C三种单体组成的体系: 分子数分别为Nay Np N。 官能度分别为f、、 单体A和C含有相同的官能团(a) 且a官能团总数少于b官能团总数(官能团b过量) 单体平均官能度按下式计算: 2(Nafa+Nefe) f Na+No++Nc NafaNefe a、b两官能团的摩尔系数r为: r= <1
两官能团不等当量--Carothers理论(3)* 两种以上单体非等物质量的情况 对于A、B、C三种单体组成的体系: 分子数分别为Na、Nb、Nc 官能度分别为fa、fb、fc 单体A和C含有相同的官能团(a) 且a官能团总数少于b官能团总数(官能团 b过量) 单体平均官能度按下式计算: ( ) a b c a a c c N N N 2 N f N f f = + + + a、b两官能团的摩尔系数 r为: <1 N f N f N f r = b b a a+ c c

单体C的a官能团数占a总数的分率为p,则 Nefe Nafa+Nefe 0二 r三 <1 NafaNcfe Nifo f- 2(Nafa+Nefe) Na+Nb+Nc 2rfafofe 将r、p式代入则: f fafe +rpfafb+r(lp)fofe fa=2,。>2的情况较多,代入上式,化简 f- 4rfe fe+2rp+r(1p)fe 两官能团不等当量-Carothersa理论
将r、 式代入则: fa = fb= 2,fc > 2 的情况较多,代入上式,化简 单体C的a官能团数占a总数的分率为 ,则 a a c c c c N f N f N f + = a c a b b c a b c f f r f f r(1 )f f 2rf f f f = + + - c c c f 2r r(1 )f 4rf f = + + - ( ) a b c a a c c N N N 2 N f N f f = + + +

代入Carothers方程,化简 Po=- 2 2r fe 此式是两官能团不等当量时,计算凝胶点的关系式 讨论: 使用此式时应注意 体系:f=fb=2,f>2 体系中a官能团数小于b P是对官能团a的反应程度而言 记住和p的特定关系式 2 ●可直接计算出单体的平均官能度,代入Pc= f 两官能团不等当量-Carothers理论
代入Carothers方程,化简 c c 2r f 1 2 1 P = + + - 此式是两官能团不等当量时,计算凝胶点的关系式 讨论: 使用此式时应注意 体系:fa = fb = 2,fc >2 体系中a官能团数小于b Pc是对官能团a的反应程度而言 记住 r和 的特定关系式 可直接计算出单体的平均官能度,代入 f 2 Pc =
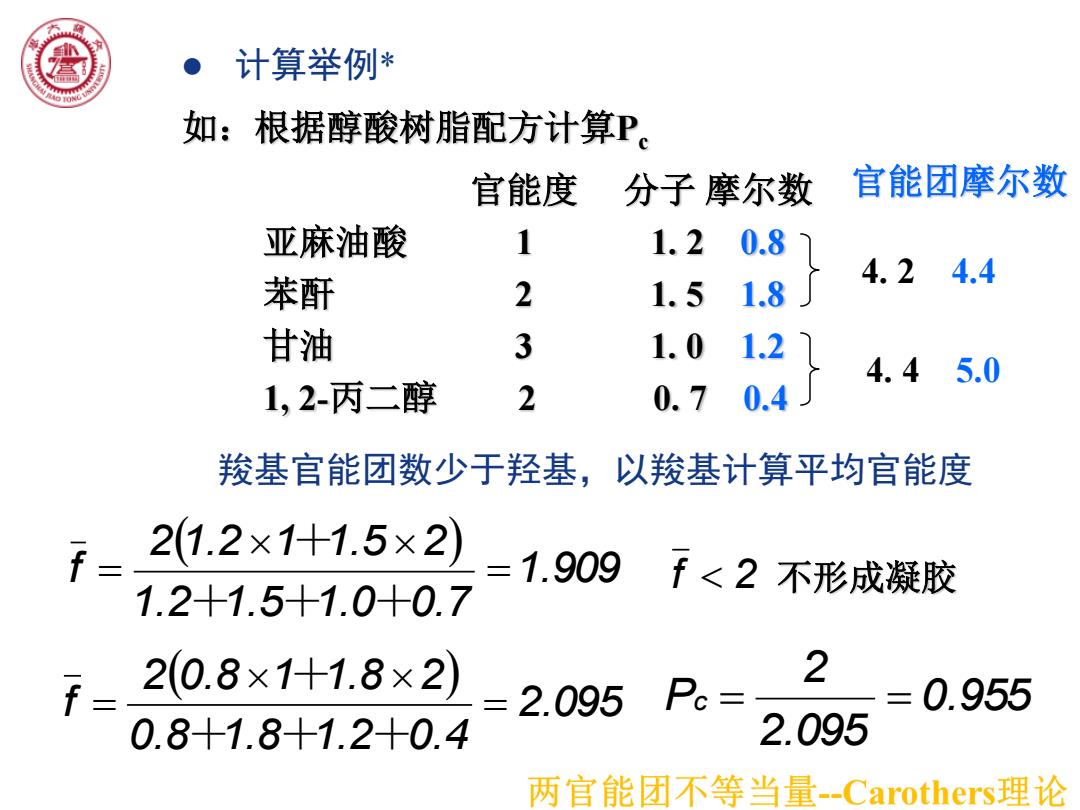
●计算举例* 如:根据醇酸树脂配方计算P。 官能度 分子摩尔数 官能团摩尔数 亚麻油酸 1 1.20.8 4.24.4 苯酐 2 1.5 1.8 甘油 3 1.0 1.2 4.45.0 1,2-丙二醇 2 0.70.4 羧基官能团数少于羟基,以羧基计算平均官能度 f- 2(1.2×1+1.5×2) =1.909f<2不形成凝胶 1.2+1.5+1.0+0.7 f- 20.8×1+1.8×2) 2 = 2.095Pc =0.955 0.8+1.8+1.2+0.4 2.095 两官能团不等当量-Carothers?理论
羧基官能团数少于羟基,以羧基计算平均官能度 计算举例* 如:根据醇酸树脂配方计算Pc 官能度 分子 摩尔数 亚麻油酸 1 1. 2 0.8 苯酐 2 1. 5 1.8 甘油 3 1. 0 1.2 1, 2-丙二醇 2 0. 7 0.4 1.909 1.2 1.5 1.0 0.7 2 1.2 1 1.5 2 f + + + + 4. 2 4.4 4. 4 5.0 官能团摩尔数 2.095 0.8 1.8 1.2 0.4 2 0.8 1 1.8 2 f + + + + 0.955 2.095 2 Pc f 2 不形成凝胶