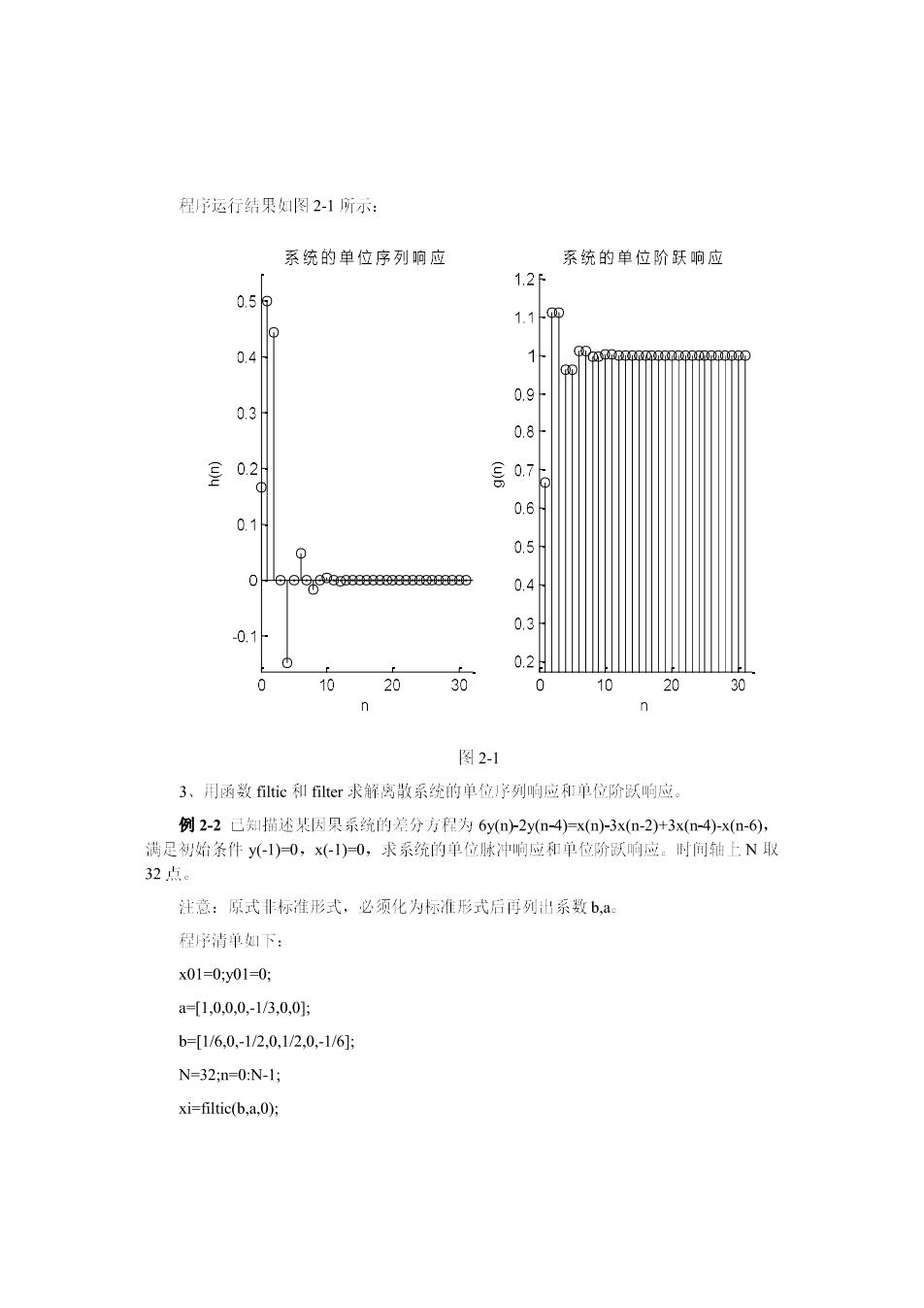
程运行结果如图21所示: 系统的单位序列响应 系统的单位阶跃响应 1.25 0.5p 1.1 0.g 0.3 02 0.7 03 10 2 30 图2-1 3、用函数ic和ter求舒离散系统的单位序列响应和单位阶跃响应。 例2-2己知描述某装因具系统的差分方程为6y2y(n-4)-x(3xn-2+3x(n4)-x(n-6), 满是初站条件y1)0,x)0,求系统的单位味冲响应和单位阶跃响应。时间轴上N取 32点。 注意:原式非标准形式,必须化为标准形式后再列出系数b,a 程序清单如下: x01=0y010 a-1,0.0.0-13.00 b16.0,-12,0,1/2.0-161 N=32:n-0:N-1; xi=filtic(b,a0方

hn-filter(b.a.x1,xi): x2-[n>-0: gn-filter(b.a.x2.xi); subplot(1.2.1):stem(n.hn.'k): tile系统的单位序列响应): ylabel(h(n)):xlabel(n); axis([0.N.1.1*min(hn).1.1*max(hn)J): subplot(1.2.2):stem(n.gn.k); title((系统的单位阶跃响应): ylabel(g(n));xlabel(n'); axis([0.N.1.1*min(gn).1.1*max(gn)J); 程疗运行结果如图2-2所示:

系统的单位序列响应 系统的单位阶跃响应 0.6 02 0 03 0.3 20 30 20 图2-2 4、用MATLAB实现线性卷积 1)用函致conv进行卷积运算: 求解两个序列的卷积和,关键在于如何确定卷积结果的时宽区间。MATLAB提供的 求卷积的数cov默认两个学列的序号均从n=0开始,卷积结果y对应的序列的序号也从 n0开始 例2-3已知两个子列f0.800<m<20),f2um)(0<<10),求两个序列的卷积和 nl-0:20: f1-0.8.ml subplot(2.2.1);stem(nI,fl,filled) title(fI(n)); n20:10: N2=length(n2); f2-ones(1,N2);
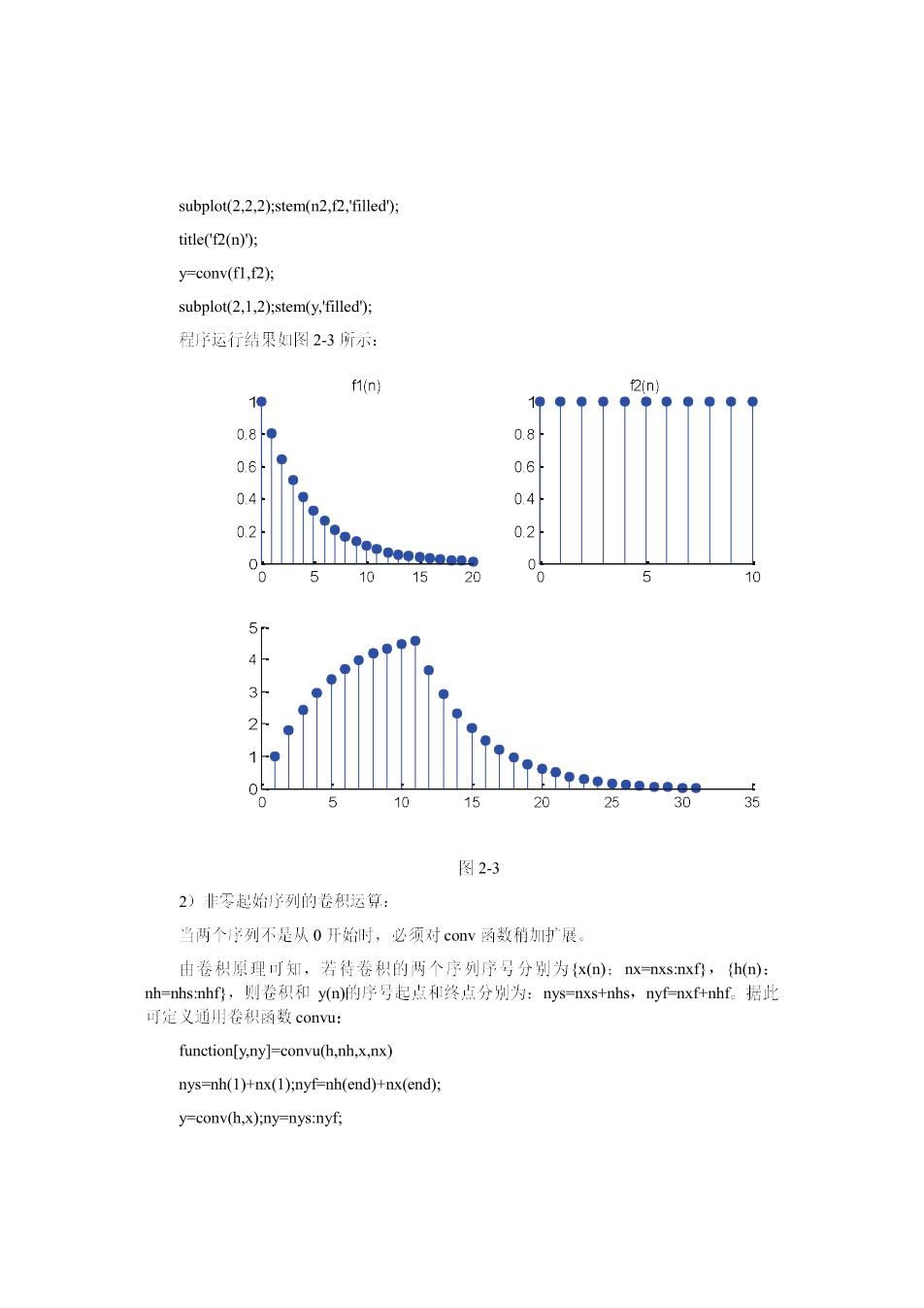
subplot(2.2.2):stem(n2.L2.filed): title(f2(n)); y-conv(f1,f2 subplot(2.1.2);stem(y.filled); 程宇运行结果如图2-3所示: f(n) 1像 0 0 06 0 0, 0.2 03 10 15 10 45 20 图2-3 2)非零起始子列的卷积运算: 当两个序列不是从0开始时,必须对comv函数稍加扩展。 由卷积原理可知,若待卷积的两个序列序号分别为xm:-nxs:nxf,(): -sh,则卷积和的序号起点和终点分为:+ns,ynh据此 可定义通用卷积函数comu: function[y.ny]-convu(h.nh.x.nx) nys-nh(1)+nx(1):nyf-nh(end)+nx(end): y-conv(h,x):ny-nys:nyf;
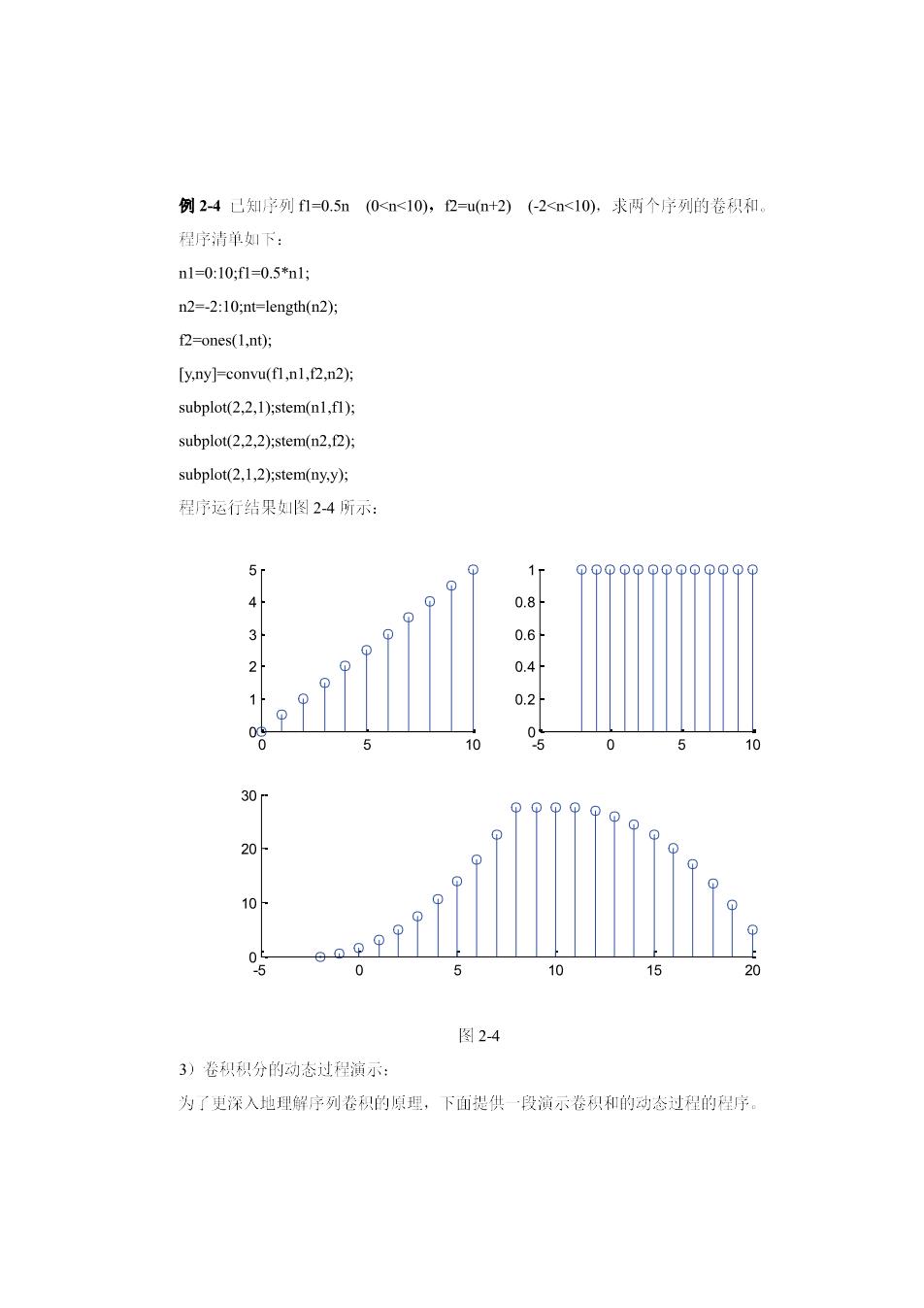
例24已知序列1-0.5n(0<<10),2=u+2)(-2<n<10),求两个序列的卷积和 程字清单如下: nl-0.10,f1=0.5*m1g n2--2:10:nt-length(n2) f2=ones(1.nt): [y.ny]-convu(f1,nI.f2.n2); subplot(2.2.I):stem(nI.f1): subplot(2.2.2).stem(n2.f2): subplot(2.1.2):stem(ny.y): 程序运行结果划图2-4所示: 5 0 图24 3)卷积积分的动态过程演示 为了更深入地理解序列卷积的原理,下面提供段演示卷积和的动态过程的程序