
例25动态演示例2-3两个序列-0.8(0<n<20),6=u)(0<n<10)的卷积和 程宇清单!下 nf1-0:20 f10.8.ml If1-length(n1); nf2-0:10 If2=length(n2); f2=oncs(I.lf2); m=max2,方 if If2>lf1 nf2-0:nf1=If2-If1; elseif If2<fl nfl=0:nf2=If1-If2: else nf:lf1-0; end; 北m u-[zeros(1.It).f2.zeros(1,nf2).zeros(1,It)]: t1-(t+1:2 fl-[zeros(1,2*It),fl,zeros(1,nf1)]; hf=fliplr(f)方 N=length(hfl); y=zeros(1,3*It); for k=0:2*It p-[zeros(1.k).hf1(1:N)]: yl=u.'p; yk=sum(y1); y(k+lt+1)=yk subplot(4.l,I):stem(tl,u): subplot(4.1.2):stem(tl.p):
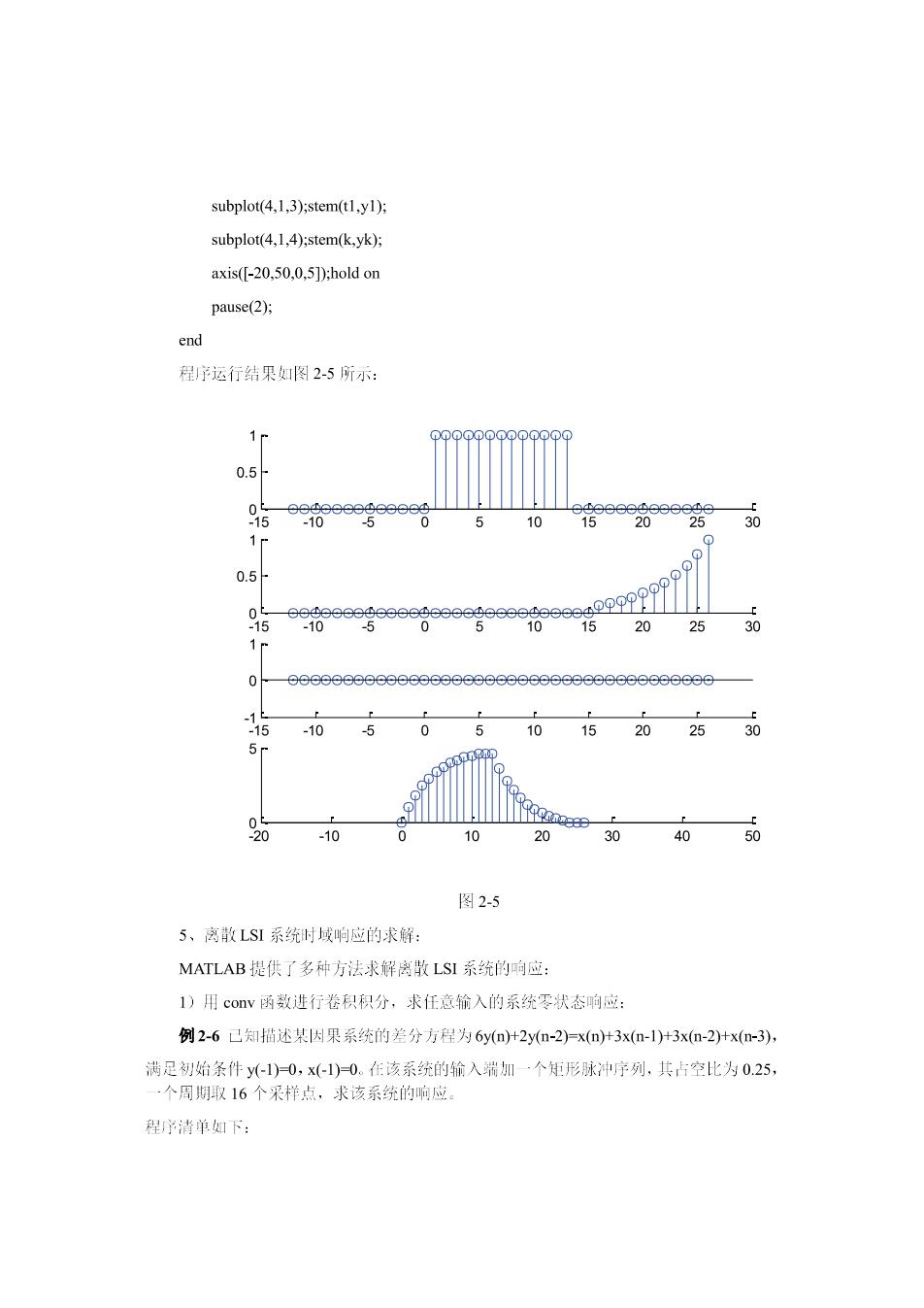
subplot(4.l.3):stem(tI.y1): subplot(4,1.4);stem(k.yk): axis([-20.50.0.5]):holdon pause(2) end 程运行结果如图2-5所示: 1 0.5 -10 15 2025 30 0.5 26 15 20 2530 20 10 10 20 30 40 50 图2-5 5、离敬LS1系统时域响应的求解: MATLAB提供了多种方法求解离散LSI系统的响应: 1)用cov函数进行卷积积分,求任意输入的系统零状态响应: 例2-6已知描述某因果系统的差分方程为6y(o)+2y-2)x(+3x(-l)+3x-2)+x(n-3) 满足始条件y)=0,x1)=0.在该系统的输入指加·个矩形脉冲序列,其占空比为0.25 ·个周期取16个采样点,求该系统的响应。 程子清单如下:
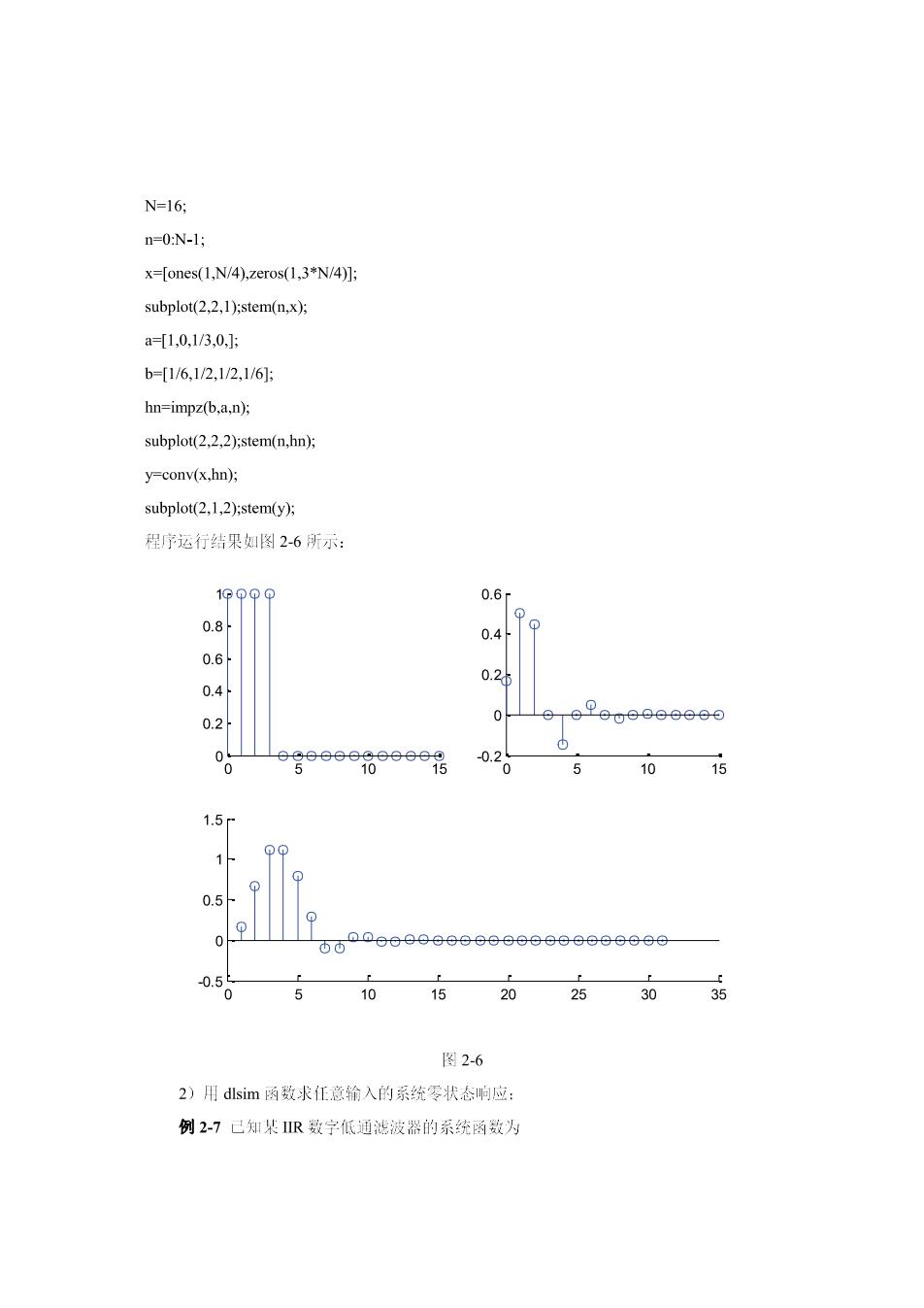
N=16: n-0:N-l; x=fones(1.N/4).zeros(1.3*N/4)]; subplot(2.2.l):stem(n.x). a1.0.1/3.0,: b-1/6,1/2,1/2,1/6 hn=impz(b.a.n) subplot(2.2.2):stem(n.hn): y=conv(x.hn); subplot(2.1.2):stem(y); 程疗运行结果如图2-6所示: 0.8 0.4 0.6 02$ 0.4 0.2 0.2 1015 1.5 0.5 0.5 5 20 25 图2-6 2)用dsim函数求任意输入的系统罗状态响应 例2-7已知某数字低通滤波器的系统函数为

HK2)-01321039637'+039632+03121E 1-0.343192+0.60439z+-0204072 箱入两个正弦叠如的学列x=sn号n0,求该系做的的, 程子清单如下: nx-0:8*pi; x=sin(nx/2)+sin(10*nx)/3; subplot(3.l.1):stem(nx.x): a-[1,-0.34319.0.60439,-0.20407 b0.1321,0.3963.0.3963,0.1321: nh-0:9:h-impz(b.a.nh); subplot(3.1,2);stem(nh.h); y-dlsim(b.a.x); subplot(3.I.3):stem(y): 程疗宇运行结果如图2-7所示
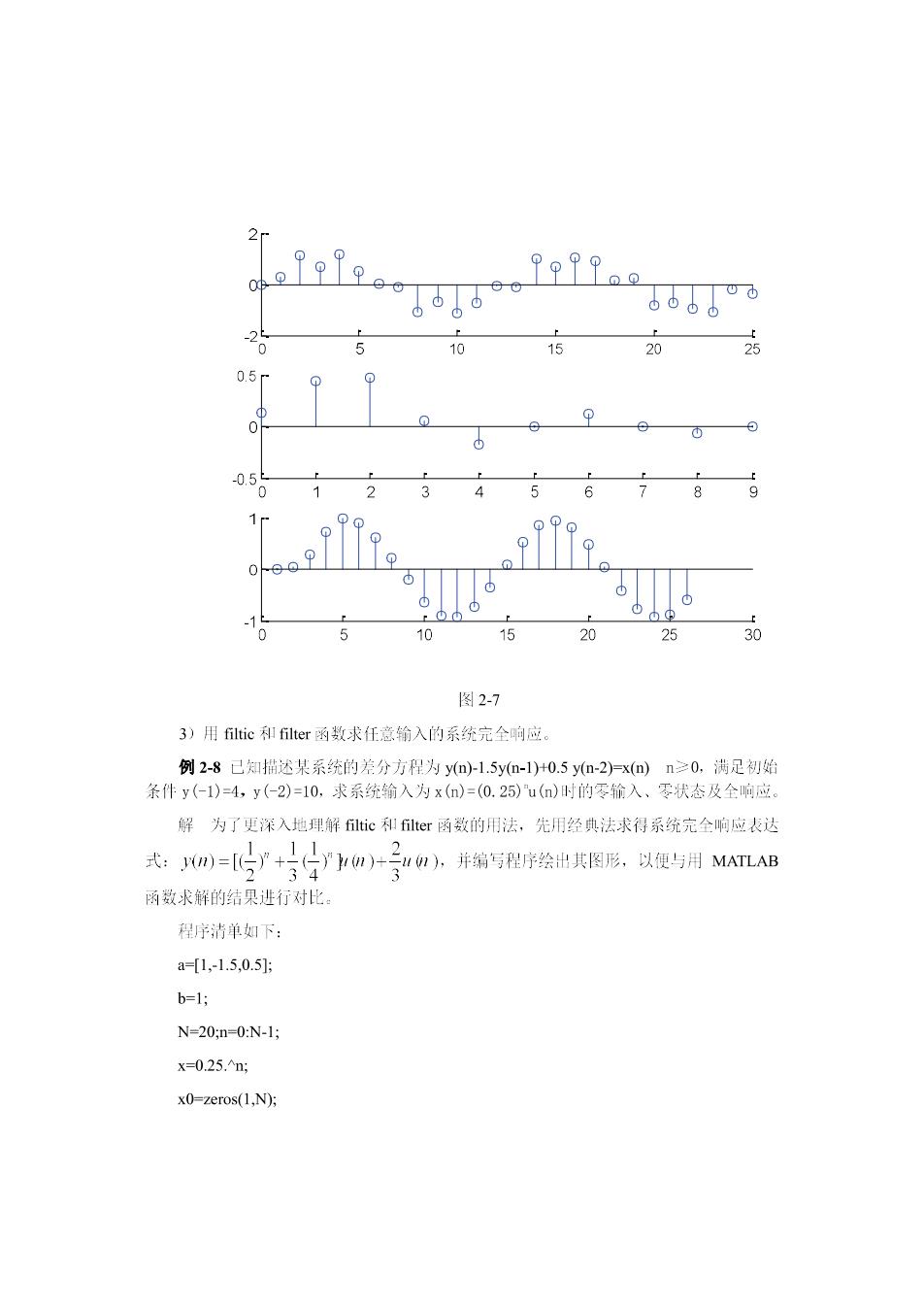
2r 9φ99 660706 0 20 25 0 6 10 20 25 30 图2-7 3)用ltic和filter函数求任意输入的系统完全响应。 例2-8已知描述某系统的差分方程为ym)-1.5y-1)+0.5yn-2)x(o)n≥0.满足制始 条件y(-1)=4,y(-2)=10.求系统输入为x(m)=(0.25)u()时的零输入、零状态及全响应。 解为了更深入地理解ic和ler函数的用法,先用经典法求得系统完全响应表达 式:0m)=+片宁0m)+!,并编写程序绘出其图形.以便与用MAB 两数求解的结果进行对比。 程序清单如下: a-1,-1.5,0.5] b=1; N=20,n=0:N-l x=0.25.m; x0-zeros(1,N):