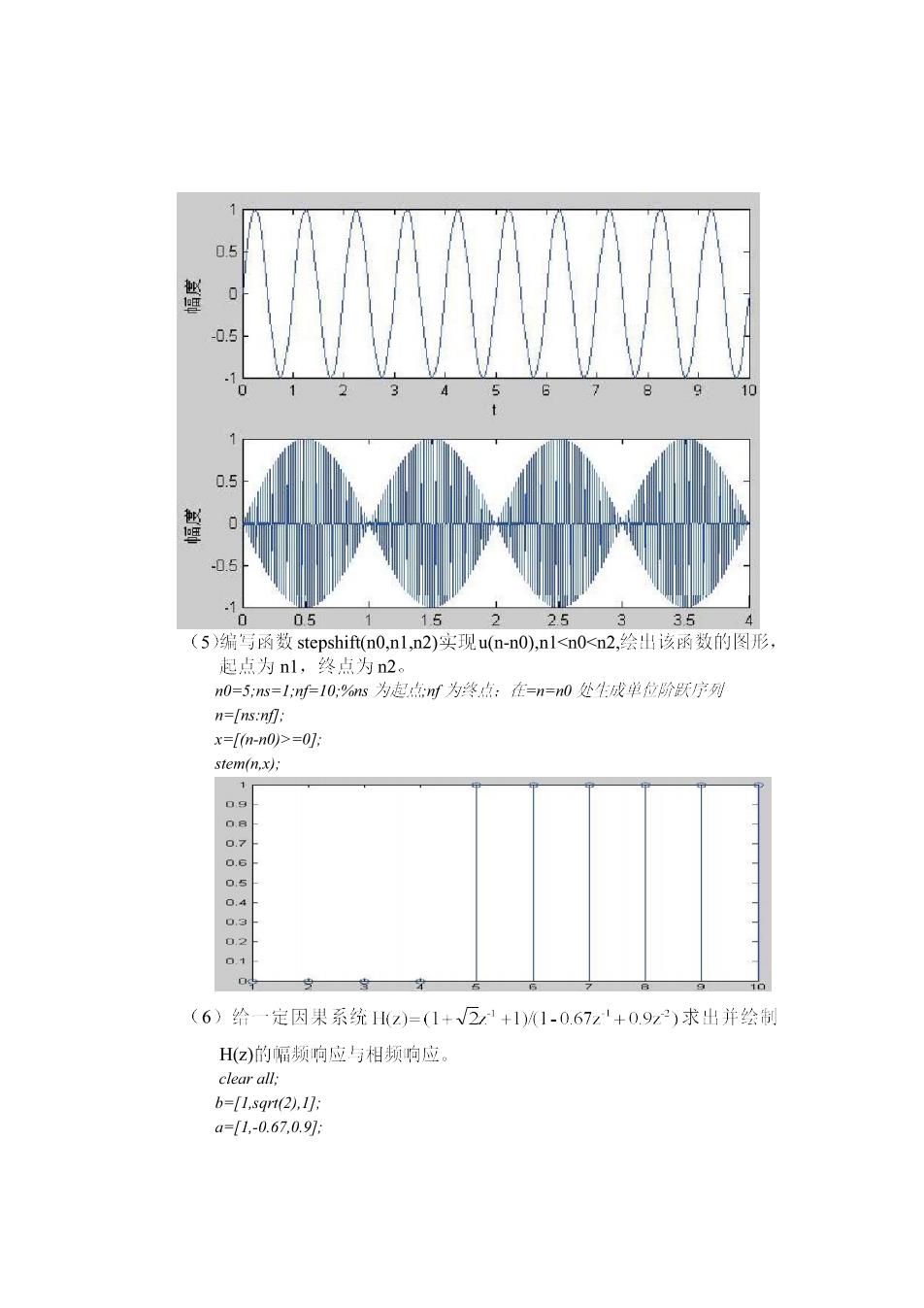
(5)编写j函数stepshift(n0,nl,n2)实现u(n-n0),nl<0<n2,绘出i该函数的图形 起点为nl,终点为n2。 n0=5s=1:n=10:%s为虑点:时为终点:在=n=n0处生成单位阶跃序列 n=[ns:nfl: x=m-0>=0 stem(n,x); o.6 0 o o (6)给一定因果系统1(2)=(1+√2+1)1.0.67z'+0.9z2)求出并绘制 H(z)的隔频向应与相频响应。 clear all: b-1,s2,1 a=.-0.67.0
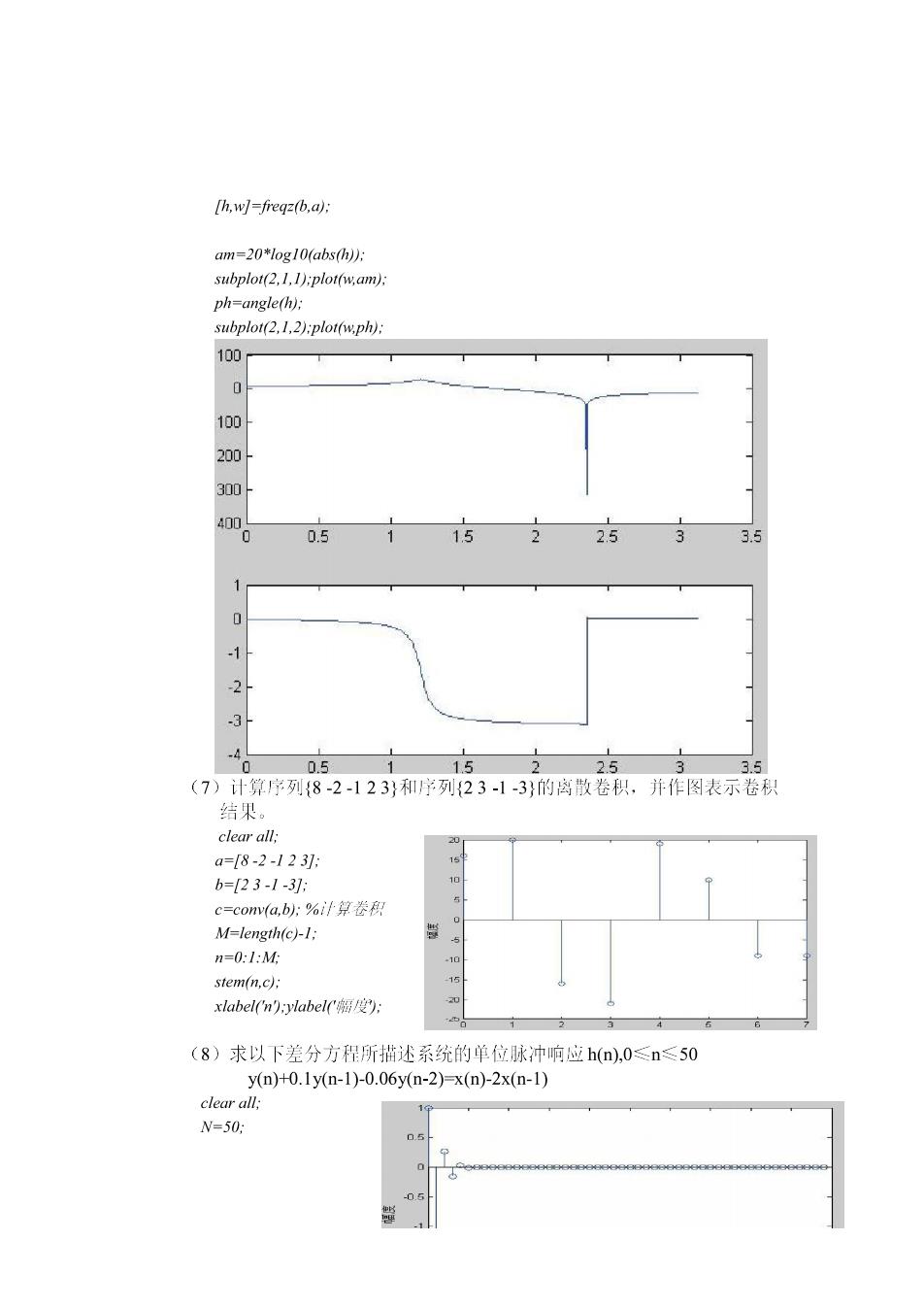
[h,wJ-freq=(b.a): an=20*1ogl0(abs(h)片 subplot(2.1,I):plot(w.am): ph=angle(h): subplor(2.1.2):plot(wph): 100 200 300 00 .1 2 3 0.5 15 25 35 (7)计算序列{8-2-123}和序列23-1-3}的离散卷积,并作图表示卷积 结果。 clear al: a=82-123 b=23-1-3 c=conv(a,b:%计算卷积 M=length(c)-1: n=0:1:M xlabel(n):ylabel度: (8)求以下差分方程所描述系统的单位脉冲响应h(n),0≤n≤50 ym)H0.1yn-1)-0.06yn-2)-x(n-2x(n-1) clear all. N=50:

a=1-2 b=101-0.06: x=(1 zeros(1.N-1)]: k=0:1-N-1 y=filter(a.b.x): xlabel(n,vlabel幅/度 两序列的位置向量不同时,序列相加的子程序:首先要使x1和x2 有同样的位置向量n:先要把x1何x2的位置向量nl和n2扩展成 包括两者最左和最右断点的公共位置向量n,然后把x1何x2放到 扩展后的位置向量n上,因为n可能比nl和n2长,必须把x1和 x2的长度加大,把加长后的x1和x2分别命名为y1和y2。这需要 把x1和x2放到位置向量n的对应位置上,并把多余的元素置零。 三、实验内容: 1、阅读并上机验证实验原理部分的例题程子,理解每一条语句的含义。 改变例题中的有关参数(如信号的衡幸、周期、幅度、最示时间的取值范围、采祥点 数等),观察对信号波形的彩响。 2、编写程子,产生以下离散子列: (1)fn)-m)(-3n<4) (2)fm-uo)(5<n<5) (3)fn)ea.1H1.sn(0<n<16) (4)fn)-3sin(nΠ/4)(0<n<20, 3、一个连续的周期性方波信号频率为200Hz,信号幅度在-1一+1V之间,要求在图形 言口上显示其两个周期的波形。以4kz的频率对连续信号进行采样,编写程序生成连实 信号和其采样获得的离敢信号波形。 四、实验预习:

1,预先阅读附录部分的MATLAB基介绍,认真阅读实验原理,明确本次实验任务 读描例恶程子,了解实验方法 2、根据实验内容预先编写实验程序。 3、预习思考题:产生单位脉冲序列和单位阶跃序列各有几种方法?如何使用? 五、实验报告 1、列写调试通过的实验程序,打印实验程序产生的曲线图形。 2、思考题:通过例题程序,你发现采样频幸Fs、采样点数N.、采样时间向隔t在程 序编写中有怎样的联系?使用时需注意什么问题? 实验2高散LSI系统的时域分析 一、实验目的: 1、加深付离敬系统的差分方程、单位脉冲响应、单位阶跃响应和卷积分析方法的理 2、初步了解用MATLAB语言进行离散时间系统时域分析的基本方法 3、学求解离散时间系统的单位脉冲响应、单位阶跃响应、线性卷积以及差分方程 的程序的编写方法,了解常用了函数的调用格式 二、实验原理: 1、离散LS1系统的响应与激恸 由离散时间系统的时域分析方法可知,一个离散LS系统的响应与激励可以用如下框 图表示:

xn] [n] 其输入、输出关系可用以下差分方程描达: 2.用函数impz和dstep求解离散系统的单位味冲响应和单位阶跃响应。 例2-1已知描述某因只系统的差分方程为6ym)+2y(m-2)xm)+3x(m-1)+3xn-2)+x(m-3) 满足初始条件y-)0,x1)0,求系统的单位脉冲响应和单位阶跃响应。 解:将y)项的系数即进行归一化,得到 y+1/3y-2)=1/6x)t1/2x(n-1)+1/2x(n-2)+1/6x(n-3) 分析上式可,这是一个3阶系统,列出其b:和系数: a-1,a1=0,a2=l/3,a30 b=16,b1=1/2,b2=1/2,b3=1/6 程序清单如下: a-1,0,1/3,01 b-lv6,1/2,V2,1/6: N=32: n=0:N-1 hn-impz(b.a.n): gn=dstep(b.a.n); subplot(1.2.1):stem(n.hn.k): tle(系统的单位序列响应) ylabel(h(n));xlabel(n); axis([0.N.1.1*min(hn).1.1"max(hn)]); subplot(1.2.2);stem(n.gn.k): itle心系统的单位阶跃用应: ylabel(g(n));xlabel(n); axis([0.N,1.1*min(gn).1.1*max(gn)]);