
·感知机是一种线性分类模型,属于判别模型。 ·感知机模型的假设空间是定义在特征空间中的所有线性 分类模型(linear classification model)或线性分类器(linear classifier),即函数集合: {flf(x)=w·x+b} 5/28
▶ 感知机是一种线性分类模型,属于判别模型。 ▶ 感知机模型的假设空间是定义在特征空间中的所有线性 分类模型(linear classification model) 或线性分类器 (linear classifier),即函数集合: {f | f (x) = w · x + b} 5 / 28
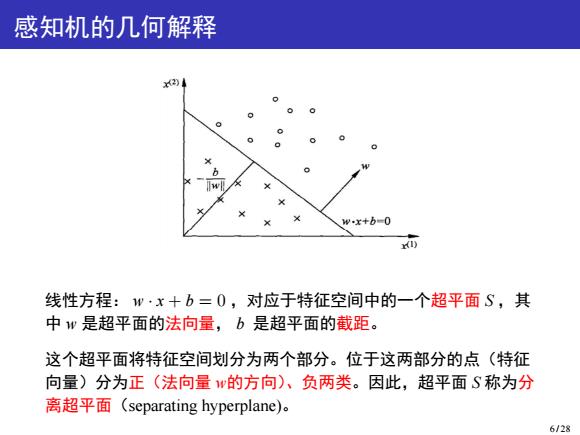
感知机的几何解释 w+x+8-0 线性方程:w·x+b=0,对应于特征空间中的一个超平面S,其 中w是超平面的法向量,b是超平面的截距。 这个超平面将特征空间划分为两个部分。位于这两部分的点(特征 向量)分为正(法向量的方向)、负两类。因此,超平面S称为分 离超平面(separating hyperplane)。 6/28
感知机的几何解释 线性方程: w · x + b = 0 ,对应于特征空间中的一个超平面 S ,其 中 w 是超平面的法向量, b 是超平面的截距。 这个超平面将特征空间划分为两个部分。位于这两部分的点(特征 向量)分为正(法向量 w的方向)、负两类。因此,超平面 S 称为分 离超平面(separating hyperplane)。 6 / 28

4.2.感知机的学习策略 数据集的线性可分性: 定义:给定一个数据集 T={(1,y1),(x2,2),,(w,w)}, 其中,∈X=R,∈y={+1,-1},i=1,2,,N,如 果存在某个超平面S w·x+b=0 能够将数据集的正实例点和负实例点完全正确地划分到超 平面的两侧,即对所有片=+1的实例有w·x:+b>0, 对所有y=-1的实例有w·x+b<0,则称数据集T 为线性可分数据集(linearly separable dataset)),否则,称数 据集T线性不可分。 7/28
4.2. 感知机的学习策略 ▶ 数据集的线性可分性: 定义:给定一个数据集 T = {(x1, y1),(x2, y2), . . . ,(xN, yN)}, 其中, xi ∈ X = R n , yi ∈ Y = {+1, −1}, i = 1, 2, . . . , N ,如 果存在某个超平面 S w · x + b = 0 能够将数据集的正实例点和负实例点完全正确地划分到超 平面的两侧,即对所有 yi = +1 的实例有 w · xi + b > 0 , 对所有 yi = −1 的实例有 w · xi + b < 0 ,则称数据集 T 为线性可分数据集(linearly separable dataset); 否则,称数 据集 T 线性不可分。 7 / 28
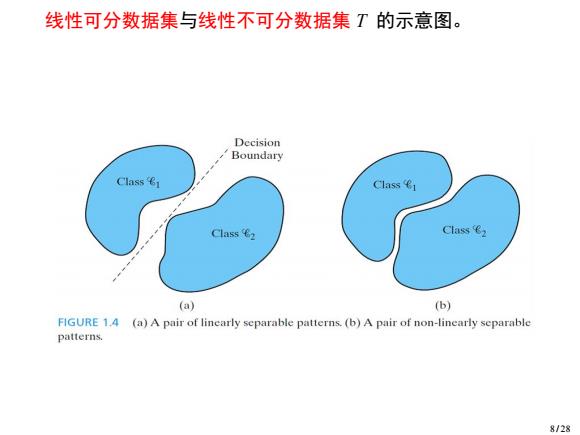
线性可分数据集与线性不可分数据集T的示意图。 Decision Boundary 1as58 Class e Class 62 Class (a) (b) FIGURE 1.4 (a)A pair of linearly separable patterns.(b)A pair of non-linearly separable patterns. 8/28
线性可分数据集与线性不可分数据集 T 的示意图。 8 / 28

感知机的学习策略 ·假设训练数据集是线性可分的,感知机学习的目标是求 得一个能够将训练集的正、负实例点完全正确分开的分离 超平面。 ·为了找出这样的超平面,即确定感知机模型参数",b, 需要确定一个学习策略,即定义(经验)损失函数,并将 损失函数极小化 ·损失函数的一个自然选择是误分类点的总数。这样的损 失函数不是参数w,b的连续可导函数,不易优化。 ·感知机所采用的损失函数是误分类点到超平面S的总距 离。 9/28
感知机的学习策略 ▶ 假设训练数据集是线性可分的,感知机学习的目标是求 得一个能够将训练集的正、负实例点完全正确分开的分离 超平面。 ▶ 为了找出这样的超平面,即确定感知机模型参数 w, b , 需要确定一个学习策略,即定义(经验)损失函数,并将 损失函数极小化. ▶ 损失函数的一个自然选择是误分类点的总数。这样的损 失函数不是参数 w, b 的连续可导函数,不易优化。 ▶ 感知机所采用的损失函数是误分类点到超平面 S 的总距 离。 9 / 28