锅炉、水轮机、水力动力比较困难,一般都采用数学模拟的方法。 原动机系统的模拟一般包括原动机特性的模拟和调速器的模拟。 原动机特性的模拟主要是机组转矩一转速静特性的模拟。一般汽轮发电机组和水轮发电 机组的转矩一转速静特性在额定转速附近都近似为45°直线,如图5所示。用方程式描述为 dMr*=一dω* 式中M一原动机转矩的标么值 ω·一原动机角速度的标么值 实验室内拖动模拟发电机的是一台普通直流电 动机,如图6所示。模拟发电机F由直流电动机 D拖动,直流电动机由三相桥式可控硅整流装置供 1 电。 为获得转矩一转速的45特性,从测速发电机弓 来的转速负反馈信号与给定值比较,又从交流侧引0 n* 来的电流反馈信号与电流调节器的给定信号进行比 图5原动机转矩一转速特性 较,经过移相、触发单元控制可控硅导通角。当控 制电压Uk增加时,整流输出电压增加,反之减小。 直流电动机 电流触 模拟发电机 部8发 测速 发电机 图6模拟原动机系统原理图 图中ZD为直流电动机:MF为模拟发电机:H为电流互感器:U:为给定电压。 模拟原动机控制系统框图见图7。 因为转矩正比于直流电动机电流1:,角速度正比于转速,所以模拟原动机系统静态特 性可用下式表示。 △I △n n。 8
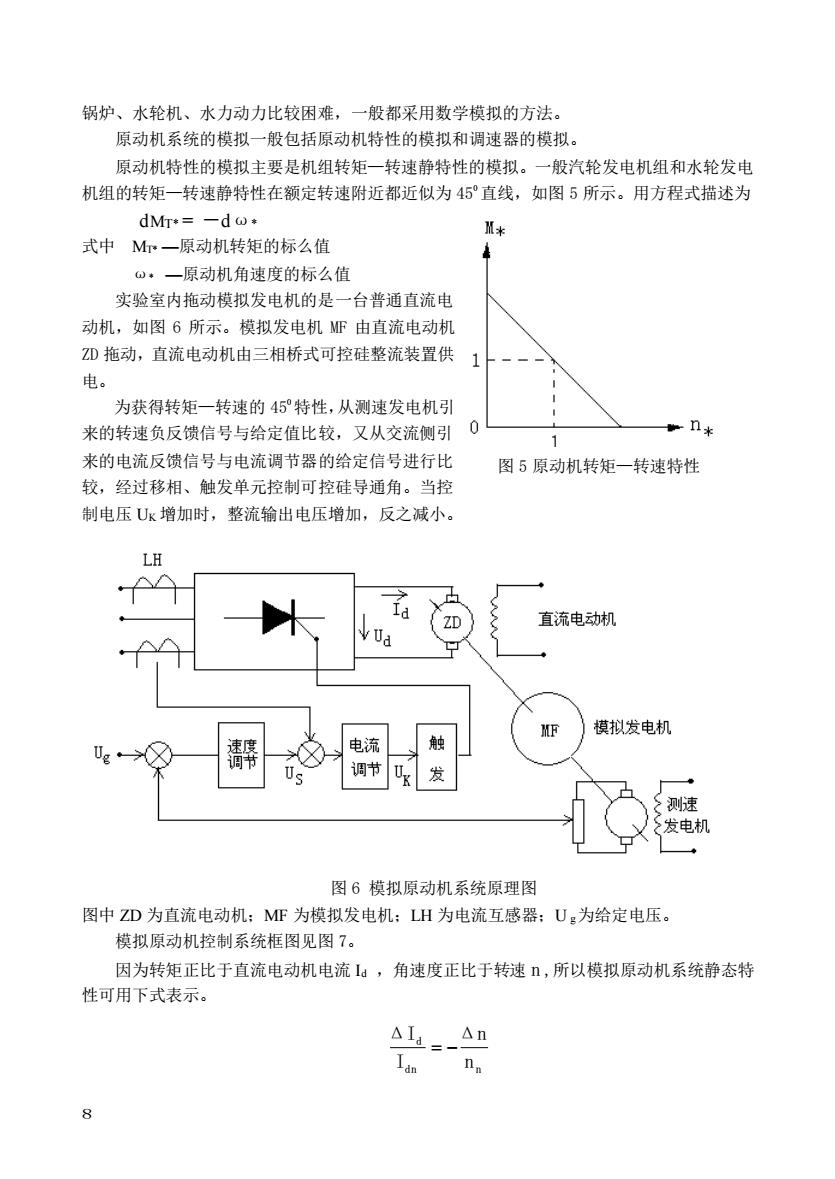
8 锅炉、水轮机、水力动力比较困难,一般都采用数学模拟的方法。 原动机系统的模拟一般包括原动机特性的模拟和调速器的模拟。 原动机特性的模拟主要是机组转矩—转速静特性的模拟。一般汽轮发电机组和水轮发电 机组的转矩—转速静特性在额定转速附近都近似为 450 直线,如图 5 所示。用方程式描述为 dMT* = -dω* 式中 MT* —原动机转矩的标么值 ω* —原动机角速度的标么值 实验室内拖动模拟发电机的是一台普通直流电 动机,如图 6 所示。模拟发电机 MF 由直流电动机 ZD 拖动,直流电动机由三相桥式可控硅整流装置供 电。 为获得转矩—转速的 450 特性,从测速发电机引 来的转速负反馈信号与给定值比较,又从交流侧引 来的电流反馈信号与电流调节器的给定信号进行比 较,经过移相、触发单元控制可控硅导通角。当控 制电压 UK 增加时,整流输出电压增加,反之减小。 图 6 模拟原动机系统原理图 图中 ZD 为直流电动机;MF 为模拟发电机;LH 为电流互感器;U g为给定电压。 模拟原动机控制系统框图见图 7。 因为转矩正比于直流电动机电流 Id ,角速度正比于转速 n ,所以模拟原动机系统静态特 性可用下式表示。 dn n d n Δn I ΔI = − 图 5 原动机转矩—转速特性
式中△L4一直流电动机电流变化量 Idm一直流电动机电枢电流额定值 △n一对应△Ld,直流电动机的转速变化量 nn一模拟发电机的额定转速 a Idn ②☒这国国3回引 品 图7模拟原动机控制系统框图 图中K,一速度调节器放大倍数 a一电流反馈量 B一速度反馈量 由图7可得控制系统电压方程式为 UaKK (U:X) (1) 电枢回路电压方程式为 U.-C.ontuR-C.0xm.nt (2) 式中CeΦn一直流电动机的电势 R一直流电动机的直流电阻 令上述(I)、(2)两式右端相等并取变化量形式(忽略Rl:和C中n变化量)可得 △4 调节反馈系数a、B和放大倍数K,使得 K,B=I 则可得到要求的原动机特性为 9
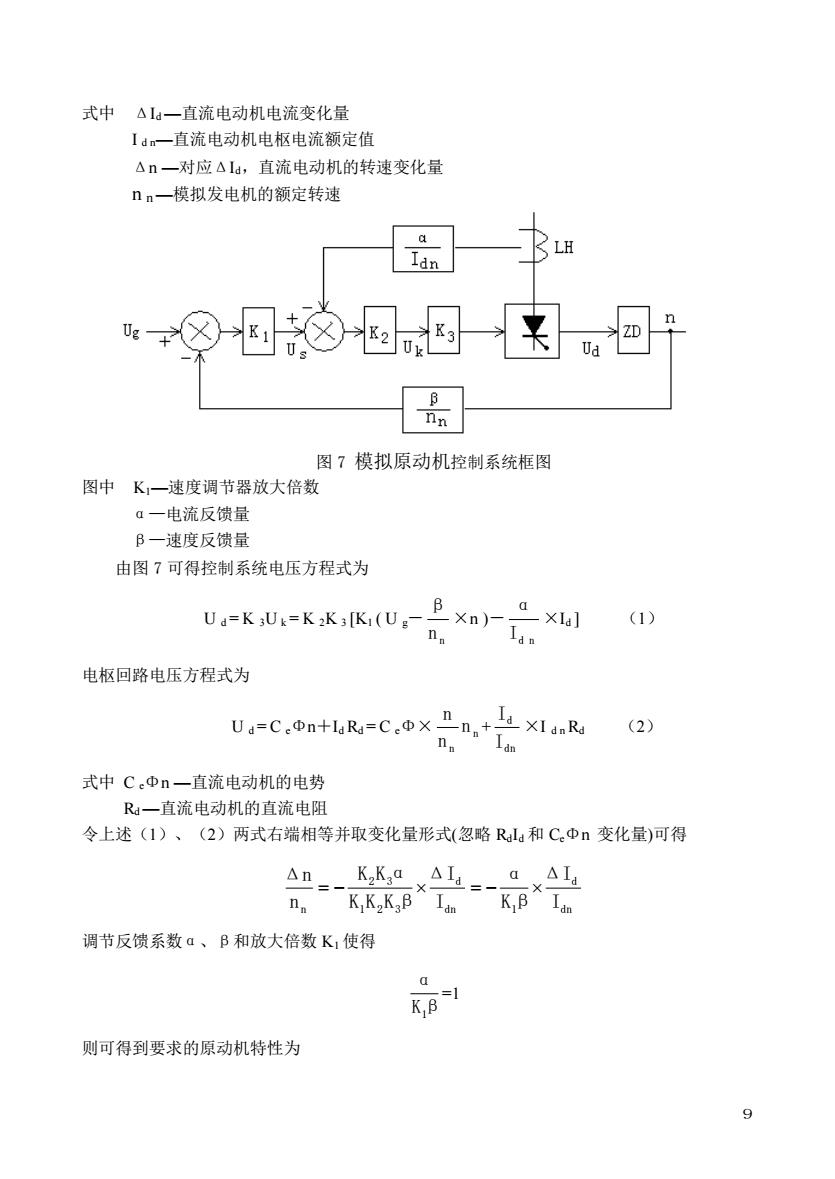
9 式中 ΔId —直流电动机电流变化量 I d n—直流电动机电枢电流额定值 Δn —对应ΔId,直流电动机的转速变化量 n n —模拟发电机的额定转速 图 7 模拟原动机控制系统框图 图中 K1—速度调节器放大倍数 α—电流反馈量 β—速度反馈量 由图 7 可得控制系统电压方程式为 U d = K 3U k = K 2K 3 [K1 ( U g- n n β ×n )- d n I α ×Id ] (1) 电枢回路电压方程式为 U d = C eΦn+Id Rd = C eΦ× n n n n n + dn d I I ×I d n Rd (2) 式中 C eΦn —直流电动机的电势 Rd —直流电动机的直流电阻 令上述(1)、(2)两式右端相等并取变化量形式(忽略 RdId 和 CeΦn 变化量)可得 dn d dn 1 d 1 2 3 2 3 n I ΔI Kβ α I ΔI K K K β K Kα n Δn = − = − 调节反馈系数α、β和放大倍数 K1 使得 Kβ α 1 =1 则可得到要求的原动机特性为

△L-40 n dMr*=一d)* 原动机调速器的模拟可参考电力系统自动化有关书籍,这里不再祥述。 另外,为更精确的模拟原动机系统的调速特性和调速器特性,微机式可控硅整流装置已 在动模得到应用。 四.模拟系统方案设计原则 要在动态模拟上对给定的原型系统进行模拟研究,首先,应确定需要模拟的原型系统, 然后,在动态模拟实验室构造一个与原型系统结构相同、参数及变量标么值相等、时间常数 相等的模拟系统,进而在模型上进行实验研究。实际电力系统是复杂的,系统结点数、支路 数、发电机台数是很多的,负荷是分散的,特性也是多种多样的。在动模实验室里,要对复 杂的电力系统原型进行完全模拟是不可能的,也是不必要的。 建立模拟系统方案时需要考虑以下问题。 1.对需要研究的课题进行分析,明确任务、性质和范围:对需要着重研究的部分,应 精确模拟,对于其它部分,可进行简化。 2.对原型系统应有深刻了解,对原型系统参数、特性及原型系统资料进行分析,对研 究影响不大或不重要的部分,进行合理简化或等值,尽量使需要模拟的原型系统规模不要太 大、太复杂。 3.应考虑实验室现有的模拟设备及其参数、特性,使得最后确定的原型系统的动态模 型是实验室可以实现的。 五.模拟计算举例 原型系统如图8所示。汽轮发电机经变压器、输电线路与无穷大系统相连,用以研究输 电线路上发生故障时系统的稳定性问题。 1.原型系统参数计算 设原型系统基准值SB=120MWA,Ug-15.75KW,则原型系统线路参数的标么值为 XL=0.387×70 2302006 120 120 1L=0.105×70 2302=Q.016 bL…=2.98×106×70 2302=0.092 120 如图9所示 10
10 dn n d n Δn I ΔI = − 即 d MT* = -dω* 原动机调速器的模拟可参考电力系统自动化有关书籍,这里不再祥述。 另外,为更精确的模拟原动机系统的调速特性和调速器特性,微机式可控硅整流装置已 在动模得到应用。 四.模拟系统方案设计原则 要在动态模拟上对给定的原型系统进行模拟研究,首先,应确定需要模拟的原型系统, 然后,在动态模拟实验室构造一个与原型系统结构相同、参数及变量标么值相等、时间常数 相等的模拟系统,进而在模型上进行实验研究。实际电力系统是复杂的,系统结点数、支路 数、发电机台数是很多的,负荷是分散的,特性也是多种多样的。在动模实验室里,要对复 杂的电力系统原型进行完全模拟是不可能的,也是不必要的。 建立模拟系统方案时需要考虑以下问题。 1.对需要研究的课题进行分析,明确任务、性质和范围;对需要着重研究的部分,应 精确模拟,对于其它部分,可进行简化。 2.对原型系统应有深刻了解,对原型系统参数、特性及原型系统资料进行分析,对研 究影响不大或不重要的部分,进行合理简化或等值,尽量使需要模拟的原型系统规模不要太 大、太复杂。 3.应考虑实验室现有的模拟设备及其参数、特性,使得最后确定的原型系统的动态模 型是实验室可以实现的。 五.模拟计算举例 原型系统如图 8 所示。汽轮发电机经变压器、输电线路与无穷大系统相连,用以研究输 电线路上发生故障时系统的稳定性问题。 1.原型系统参数计算 设原型系统基准值 SB=120MVA,UB=15.75KV,则原型系统线路参数的标么值为 Xl L* = 0.387×70× 2 230 120 = 0.06 rl L* = 0.105×70× 2 230 120 = 0.016 bl L* = 2.98×10-6×70× 120 2302 = 0.092 如图 9 所示

15.75KV 230KV 无穷大系统 发电机 变压器 线路 Sn =120MVA Sn =120MVA L=70KM Xd*=1.6 0k=12% 51=0.105/K Xd*=0.2 15.75/230KV X1=0.387/ Xd*=0.13 Yo/△-11 b1=2.98x106-K 图8原型系统接线图及参数 取原型电抗基准值 Xe"2_15.75 =2.070 120 则同步发电机电抗有名值为 Xd*=1.6 Xa=1.6×2.07=3.310 Xd*=0.2 Uk=12% L*=0.06 五L*=0.016 Xd=0.2×2.07=0.4140 Xd*=0.13 Y0/△-11 o=6” b1L*=0.092 X"d=0.13×2.07=0.270 2.模型系统参数计算与调整 图9原型系统及标么值参数 对上述原型系统发电机选用 5KVA的隐极模拟发电机进行模拟,模拟机其参数为 S n=5KVA Un=230v Im=1255A Td0=1.2 Xd*=1.25 Xd=0.13 Xd*=0.08 =6.1” 其中电抗是以S.和Un为基准值的标么值。其有名值为 光=xx -1.25×5000 2302 13.29 S。 -=0.13 5000=1.389 2302 11
11 取原型电抗基准值 XB= 2.07Ω 120 15.75 S U 2 B 2 B = = 则同步发电机电抗有名值为 Xd = 1.6×2.07 =3.31Ω X ’ d = 0.2×2.07 =0.414Ω X ” d = 0.13×2.07 =0.27Ω 2.模型系统参数计算与调整 对上述原型系统发电机选用 5KVA 的隐极模拟发电机进行模拟,模拟机其参数为 S n =5KVA Un =230v I n =12.55A Td0 =1.2” Xd* =1.25 X’ d* =0.13 X” d* = 0.08 TJ = 6.1” 其中电抗是以 S n 和 U n 为基准值的标么值。其有名值为 Xd = Xd*× 13.2Ω 5000 230 1.25 S U 2 n 2 n = = X ’ d = X ’ d*× 1.38Ω 5000 230 0.13 S U 2 n 2 n = =

X-Xx号-0o8×-050 以下讨论如何调整模拟系统参数,使之与原型系统参数标么值相等。 (1)由于 X∠X(其中下标y表示原型,下标m表示模型),可以考虑在模 X dyt X dme 拟发电机定子绕组外串电抗△X,但需满足 Xot=Xou +AX. XdsX*+△X, 把参数代入得 1.6_1.25+△X 0.20.13+△X 解得 △X.=0.03 外串电抗后模型参数 Xdm*+△X=1.25+0.03=l.28 Xdm+△X.=0.13+0.03=0.16 X“dm+△X.=0.08+0.03=0.11 这里 4X=003×2302 5000=0.320 所以外串电抗后模型参数有名值为 Xdm+△X=13.2+0.32=13.520 X'dm+△X=l.38+0.32=1.70 X"dm+△X=0.85+0.32=1.179 (2)选择模拟比 外串电抗后 X, X dy 3.31_0.414=0.244 m元x+axXa+aX8.521.7 根据空载特性在运行点相似的要求,选模拟发电机额定电压为180V,则 -0-75 计算出另外两个模拟比为 12
12 X ” d = X ” d*× 0.85Ω 5000 230 0.08 S U 2 n 2 n = = 以下讨论如何调整模拟系统参数,使之与原型系统参数标么值相等。 (1)由于 dm* ' dm* dy* ' dy* X X X X (其中下标 y 表示原型,下标 m 表示模型),可以考虑在模 拟发电机定子绕组外串电抗ΔX*,但需满足 * dm* ' dm* * dy* ' dy* X ΔX X ΔX X X + + = 把参数代入得 * * 0.13 ΔX 1.25 ΔX 0.2 1.6 + + = 解得 ΔX* = 0.03 外串电抗后模型参数 X dm* +ΔX* = 1.25+0.03 =1.28 X ‘ dm* +ΔX* = 0.13+0.03 =0.16 X “ dm* + ΔX* = 0.08 +0.03 =0.11 这里 ΔX = 0.03× = 5000 2302 0.32Ω 所以外串电抗后模型参数有名值为 X dm+ΔX =13.2+0.32 =13.52Ω X ’ dm+ΔX =1.38+0.32 =1.7Ω X” dm+ΔX =0.85+0.32 =1.17Ω (2)选择模拟比 外串电抗后 m x = 0.244 1.7 0.414 13.52 3.31 X ΔX X X ΔX X X X dm ' dy ' dm dy m y = = = + = + = 根据空载特性在运行点相似的要求,选模拟发电机额定电压为 180V,则 m v= 87.5 180 15750 = 计算出另外两个模拟比为