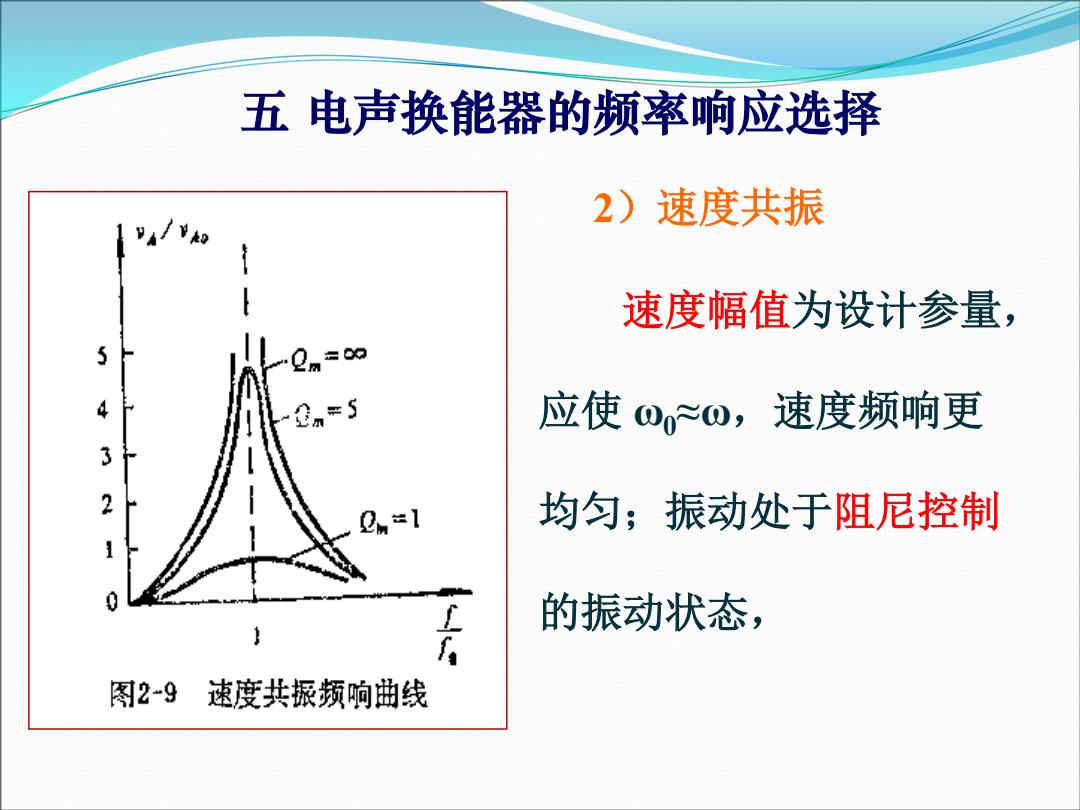
五电声换能器的频率响应选择 2)速度共振 速度幅值为设计参量, 3n*5 应使Qo,速度频响更 均匀;振动处于阻尼控制 的振动状态, 图2-9速度共振频响曲线
2)速度共振 五 电声换能器的频率响应选择 速度幅值为设计参量, 应使 ω0≈ω,速度频响更 均匀;振动处于阻尼控制 的振动状态
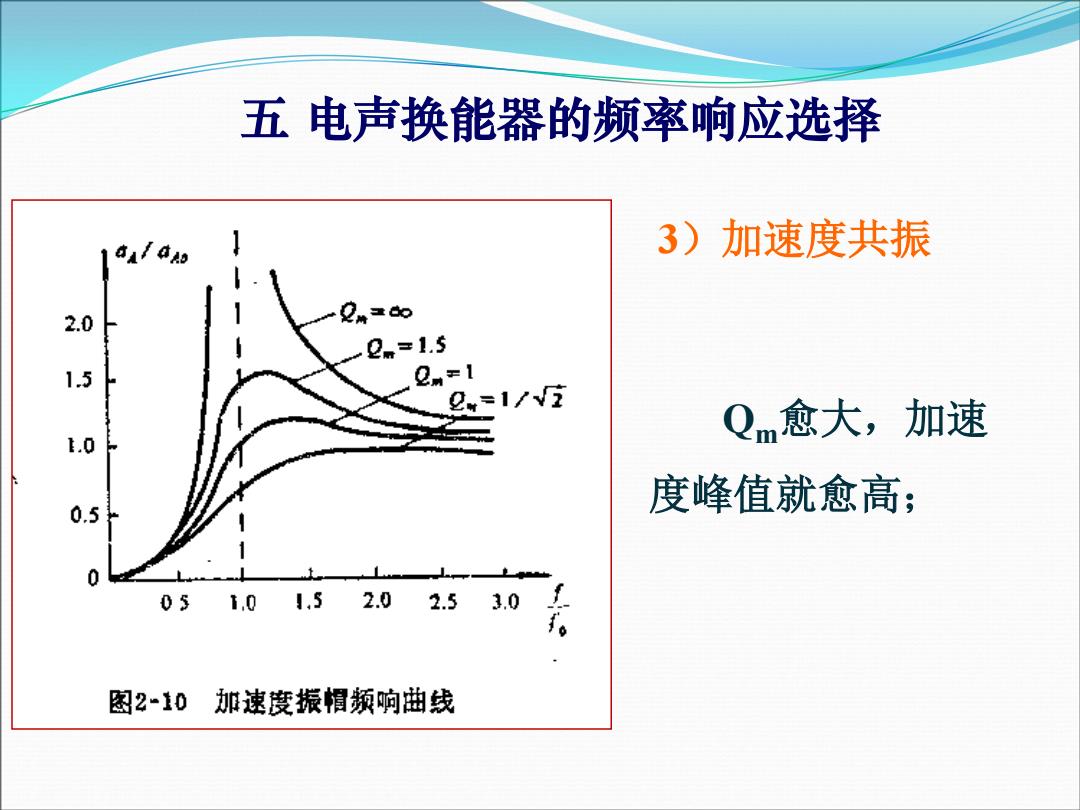
五电声换能器的频率响应选择 3)加速度共振 2.0 2m-1.5 1.5 C=1/V Qm愈大,加速 .0 度峰值就愈高; 0.5 0 0s1.01.52.02.53.0 图2-10加速度振帽频响曲线
3)加速度共振 Qm愈大,加速 度峰值就愈高; 五 电声换能器的频率响应选择
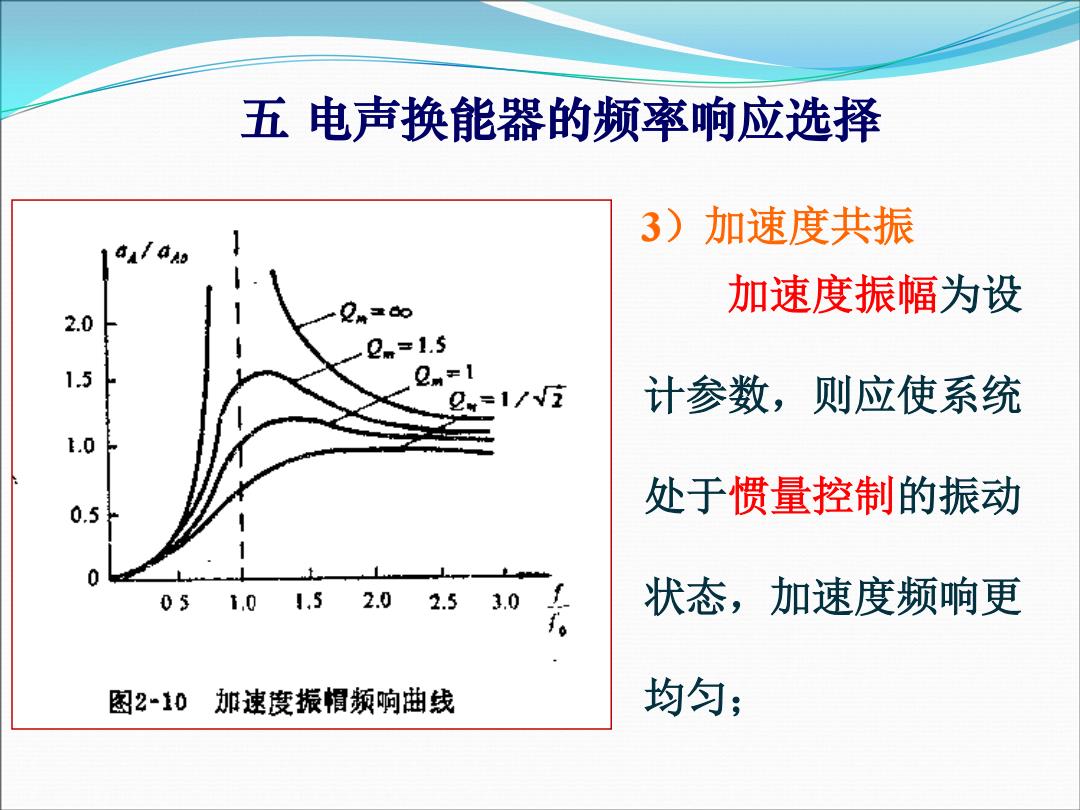
五电声换能器的频率响应选择 3)加速度共振 加速度振幅为设 2.0 2m-1.5 1.5 2m= 2w=1/√i 计参数,则应使系统 .0 处于惯量控制的振动 0.5 0 0s1.01.52.02.53.0 状态,加速度频响更 图2-10 加速度振帽频响曲线 均匀
3)加速度共振 加速度振幅为设 计参数,则应使系统 处于惯量控制的振动 状态,加速度频响更 均匀; 五 电声换能器的频率响应选择

七振动的合成 超声实际发射时,很难达到理想的集束和均 一的相位,是振动片(换能器)上各个点振动的 合成; 两个声源在媒质中某点的合成,是两个运动 的迭加,在数学上就是矢量和; 要研究的也就是合成运动的运动规律,也遵 循由简单到复杂的研究顺序;
超声实际发射时,很难达到理想的集束和均 一的相位,是振动片(换能器)上各个点振动的 合成; 两个声源在媒质中某点的合成,是两个运动 的迭加,在数学上就是矢量和; 要研究的也就是合成运动的运动规律,也遵 循由简单到复杂的研究顺序; 七 振动的合成

七振动的合成 (一)同一直线上两个同频简谐振动合成 2 72 x1=A,c0s(0t+4) x2=A2c0s(0t+中2) 则合振动的振动方程为 x=x+x2=Acos(@t+) 其中A=VA2+A,2+2A1A,c0s(中,-中,) A sin +A,sing arctg A,cos9,+A,c0s0:
(一)同一直线上两个同频简谐振动合成 七 振动的合成 其中 2 cos( ) 1 2 2 1 2 2 2 A = A1 + A + A A φ −φ 1 1 2 2 1 1 2 2 cos cos sin sin φ φ φ φ φ A A A A arctg + + = cos( ) 1 = 1 ω +φ1 x A t cos( ) 2 = 2 ω +φ2 x A t 则合振动的振动方程为 cos( ) x = x1 + x2 = A ωt +φ