
简单连通平面图的必要条件 ■欧拉公式的推论:若G是简单连通平面图(≥3),则 m≤3n-6。 口证明:至少3个顶点的简单图G中,面的最小边数是3, ∴.3r≤2m,根据欧拉公式:3r=3m+6-3n,∴.3m+6-3n<2m,即: m≤3n-6。 ■K不是平面图:在K中,n=5,m=10,3n-6=9。 平面图中,边数是有上限的。请问,这个界是否紧致?
简单连通平面图的必要条件 ◼ 欧拉公式的推论:若G是简单连通平面图(n3), 则 m3n-6。 ❑ 证明:至少3个顶点的简单图G中,面的最小边数是3, 3r2m, 根据欧拉公式:3r=3m+6-3n, 3m+6-3n2m, 即: m3n-6。 ◼ K5不是平面图:在K5中,n=5,m=10, 3n-6=9。 平面图中,边数是有上限的。请问,这个界是否紧致?

问题4: 上述推论不能证明K33是非平面图 你能推出一个类似的推论用于K3.3吗? 二部图的一个区 域至少多少条边?
二部图的一个区 域至少多少条边?
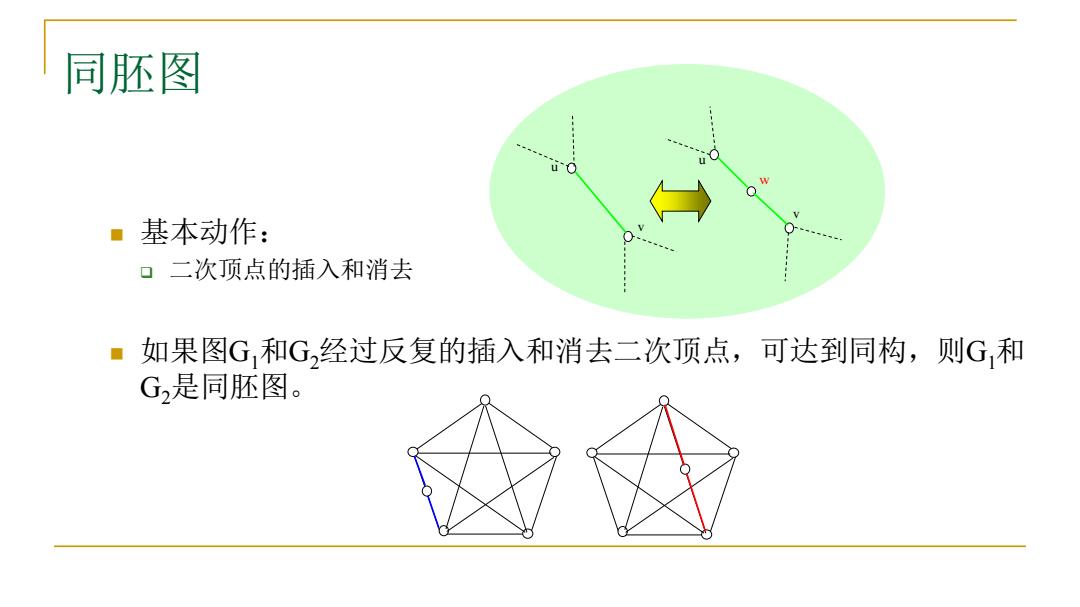
同胚图 u ·基本动作: 口二次顶点的插入和消去 。 如果图G,和G经过反复的插入和消去二次顶点,可达到同构,则G,和 G,是同胚图
同胚图 ◼ 基本动作: ❑ 二次顶点的插入和消去 ◼ 如果图G1和G2经过反复的插入和消去二次顶点,可达到同构,则G1和 G2是同胚图。 u u v v w
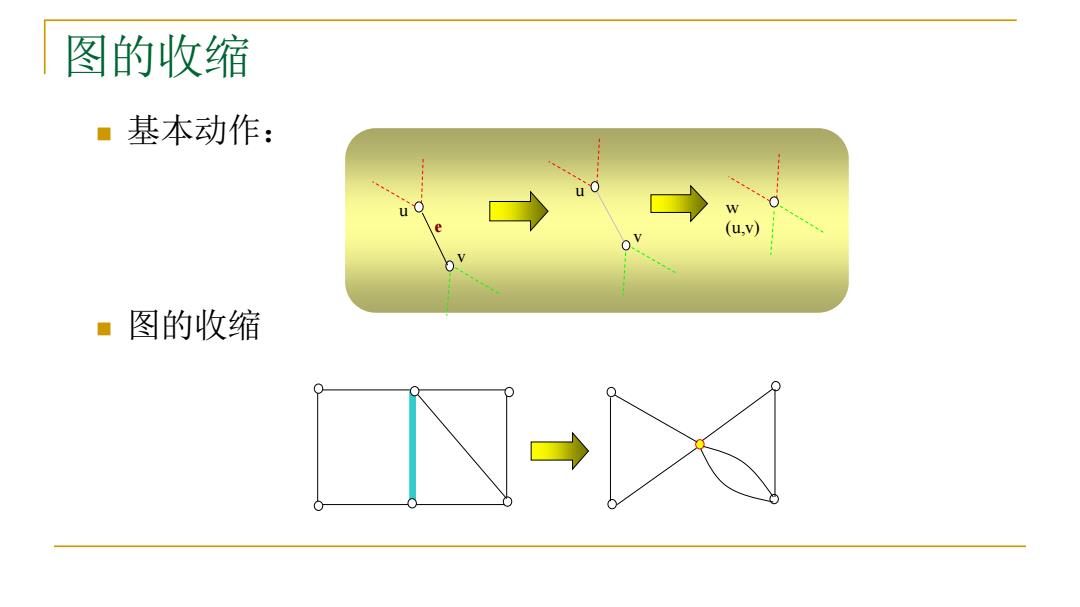
图的收缩 ■基本动作: u O u c w (u,V) ■图的收缩
图的收缩 ◼ 基本动作: ◼ 图的收缩 u v u v e w (u,v)

平面图的充分必要条件 Kuratowsky定理 o 图G是平面图当且仅当G中不含与K或者K,3同胚的子图,也不含可以 收缩到K或者K33的子图
平面图的充分必要条件 ◼ Kuratowsky定理 ❑ 图G是平面图当且仅当G中不含与K5或者K3,3同胚的子图,也不含可以 收缩到K5或者K3,3的子图