
Introduction to Steady State (AC)Analysis More generally,use the Fourier Transform For a periodic function v(t)with period T,the Fourier Transform is defined as: 乎[v(t】=VGo)='v(t)ejot dt where j=v-1 Some important Transforms ·v(t)=Vp cos(oot) V(jo) Vpπ A 0 -00 VGo)) ◆v(t)=Vp sin(oot) Vpπ A 0 -00 Generally,we will ignore the negative frequency space... Basic Electronics-Special Lecture for TIPP 2011 11 Gary Drake,Argonne National Lab-Session 2
Basic Electronics – Special Lecture for TIPP 2011 11 Gary Drake, Argonne National Lab – Session 2 Introduction to Steady State (AC) Analysis More generally, use the Fourier Transform • For a periodic function v(t) with period T, the Fourier Transform is defined as: • Some important Transforms F [v(t)] = V(j) = f v(t) ejt dt h VP O O t v(t) = VP cos(Ot) VP -VP where j = S -1 -h VP V(j) v(t) = VP sin(Ot) VP O O t VP -VP VP V(j) Generally, we will ignore the negative frequency space…

Introduction to Steady State (AC)Analysis Fourier Transform Properties For a periodic function v(t)with period T,the Fourier Transform is defined as: 牙vt】=VGo)=∫v()eimt dt wherej=V-l The Inverse Fourier Transform is given as: g乎VGo】=v()=1/(2m)/VGo)eiot do An important Transform property that we will use: g乎[d/dtv(tj=jo Vjo) Fourier Transforms generally generate Complex Numbers... Basic Electronics-Special Lecture for TIPP 2011 12 Gary Drake,Argonne National Lab-Session 2
Basic Electronics – Special Lecture for TIPP 2011 12 Gary Drake, Argonne National Lab – Session 2 Introduction to Steady State (AC) Analysis Fourier Transform Properties • For a periodic function v(t) with period T, the Fourier Transform is defined as: • The Inverse Fourier Transform is given as: • An important Transform property that we will use: F [v(t)] = V(j) = f v(t) ejt dt h F [d/dt v(t)] = j V(j) where j = S -1 -h F-1 [V(j)] = v(t) = 1/(2 f V(j) ejt d h -h Fourier Transforms generally generate Complex Numbers…

Introduction to Steady State (AC)Analysis A Review of Complex Numbers ·For F(j)=aREAL j bIMAG Think of Complex Plane IMAG F(jo) b FGo)=aREAL2+bIMAG2 -REAL φ=tanl[bMAu/aREAL These are related to Phasors Phasor form:FG)=FGw) F(jo)=Mag /Angle Basic Electronics-Special Lecture for TIPP 2011 13 Gary Drake,Argonne National Lab-Session 2
Basic Electronics – Special Lecture for TIPP 2011 13 Gary Drake, Argonne National Lab – Session 2 Introduction to Steady State (AC) Analysis A Review of Complex Numbers • For • Think of Complex Plane • These are related to Phasors Phasor form: F(j) = F(jw) F(j) = aREAL + j bIMAG F(j) = Mag Angle = w aREAL2 + bIMAG2 = tan-1 [bIMAJ / aREAL] IMAG REAL F(j) F(j) a b
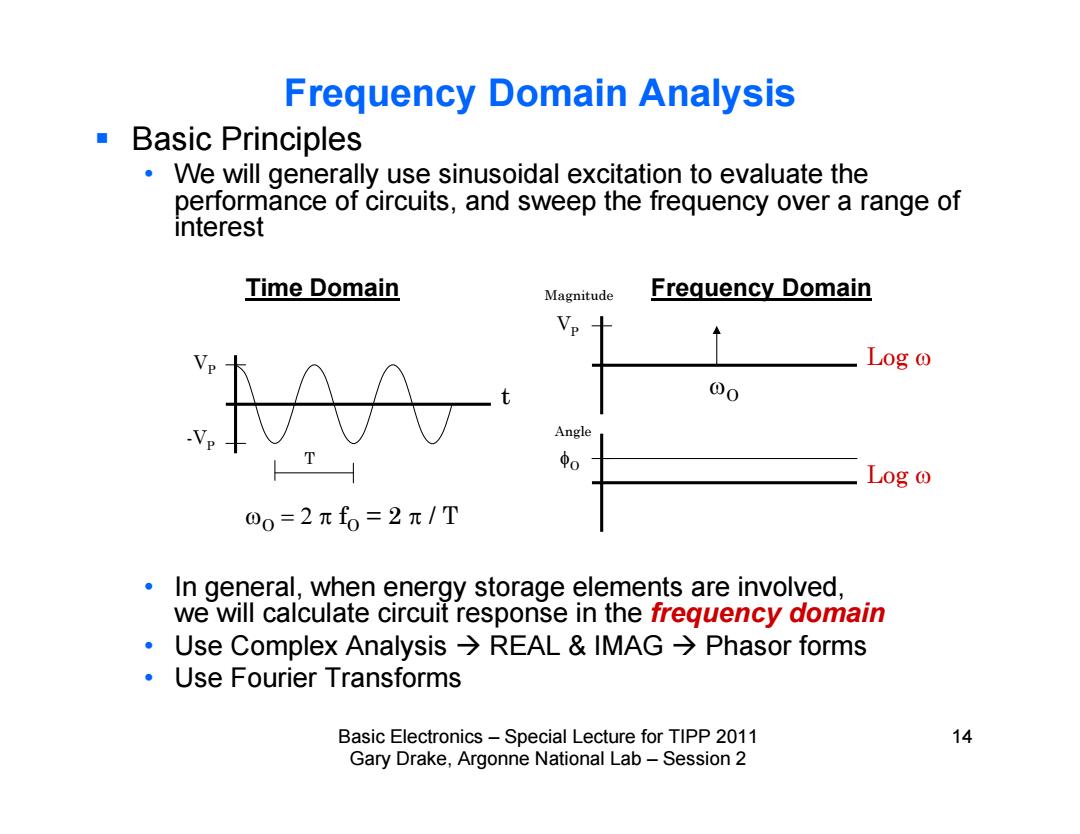
Frequency Domain Analysis ■Basic Principles We will generally use sinusoidal excitation to evaluate the performance of circuits,and sweep the frequency over a range of interest Time Domain Magnitude Frequency Domain VP Log o 0 Angle Log o 00=2π0=2π/T In general,when energy storage elements are involved, we will calculate circuit response in the freguency domain ·Use Complex Analysis→REAL&lMAG→Phasor forms Use Fourier Transforms Basic Electronics-Special Lecture for TIPP 2011 14 Gary Drake,Argonne National Lab-Session 2
Basic Electronics – Special Lecture for TIPP 2011 14 Gary Drake, Argonne National Lab – Session 2 Frequency Domain Analysis Basic Principles • We will generally use sinusoidal excitation to evaluate the performance of circuits, and sweep the frequency over a range of interest • In general, when energy storage elements are involved, we will calculate circuit response in the frequency domain • Use Complex Analysis REAL & IMAG Phasor forms • Use Fourier Transforms t VP T -VP Log VP Log O O Time Domain Magnitude Frequency Domain Angle O fO = 2 / T