
Load Balancing:LPT Rule Longest processing time (LPT).Sort n jobs in descending order of processing time,and then run list scheduling algorithm. LPT-List-Scheduling (m,n,t1,t2,...,t){ Sort jobs so that t1≥t2之.≥tm for i=1 to m 工1←0 load on machine i J(i)←中 -jobs assigned to machine i } for j=1 to n i=argmink Lk machine i has smallest load J(i)←J(i)U{j} assign job j to machine i 工1←工:+七5 ★一 update load of machine i return J(1),…,J(m) 业
11 Load Balancing: LPT Rule Longest processing time (LPT). Sort n jobs in descending order of processing time, and then run list scheduling algorithm. LPT-List-Scheduling(m, n, t1,t2,…,tn) { Sort jobs so that t1 ≥ t2 ≥ … ≥ tn for i = 1 to m { Li 0 J(i) } for j = 1 to n { i = argmink Lk J(i) J(i) {j} Li Li + tj } return J(1), …, J(m) } jobs assigned to machine i load on machine i machine i has smallest load assign job j to machine i update load of machine i

Load Balancing:LPT Rule Observation.If at most m jobs,then list-scheduling is optimal. Pf.Each job put on its own machine.- Lemma 3.If there are more than m jobs,L*>2tm+1. Pf. Consider first m+1 jobs t1,...,tm+1. Since the ti's are in descending order,each takes at least tm+1 time. There are m+1 jobs and m machines,so by pigeonhole principle,at least one machine gets two jobs." Theorem.LPT rule is a 3/2 approximation algorithm. Pf.Same basic approach as for list scheduling. L,=(L,-)+4≤多L*.· ≤L* ≤号L* ↑ Lemma 3 by observation,can assume number of jobs m 12
12 Load Balancing: LPT Rule Observation. If at most m jobs, then list-scheduling is optimal. Pf. Each job put on its own machine. ▪ Lemma 3. If there are more than m jobs, L* 2 tm+1. Pf. Consider first m+1 jobs t1 , …, tm+1. Since the ti 's are in descending order, each takes at least tm+1 time. There are m+1 jobs and m machines, so by pigeonhole principle, at least one machine gets two jobs. ▪ Theorem. LPT rule is a 3/2 approximation algorithm. Pf. Same basic approach as for list scheduling. ▪ Li (Li t j ) L* t j 1 2 L* 3 2 L *. Lemma 3 ( by observation, can assume number of jobs > m )

Load Balancing:LPT Rule Q.Is our 3/2 analysis tight? A.No. Theorem.[Graham,1969]LPT rule is a 4/3-approximation. Pf.More sophisticated analysis of same algorithm. Q.Is Graham's 4/3 analysis tight? A.Essentially yes. Ex:m machines,n=2m+1 jobs,2 jobs of length m+1,m+2,...,.2m-1 and one job of length m. 3
13 Load Balancing: LPT Rule Q. Is our 3/2 analysis tight? A. No. Theorem. [Graham, 1969] LPT rule is a 4/3-approximation. Pf. More sophisticated analysis of same algorithm. Q. Is Graham's 4/3 analysis tight? A. Essentially yes. Ex: m machines, n = 2m+1 jobs, 2 jobs of length m+1, m+2, …, 2m-1 and one job of length m

5.2 Center Selection
5.2 Center Selection
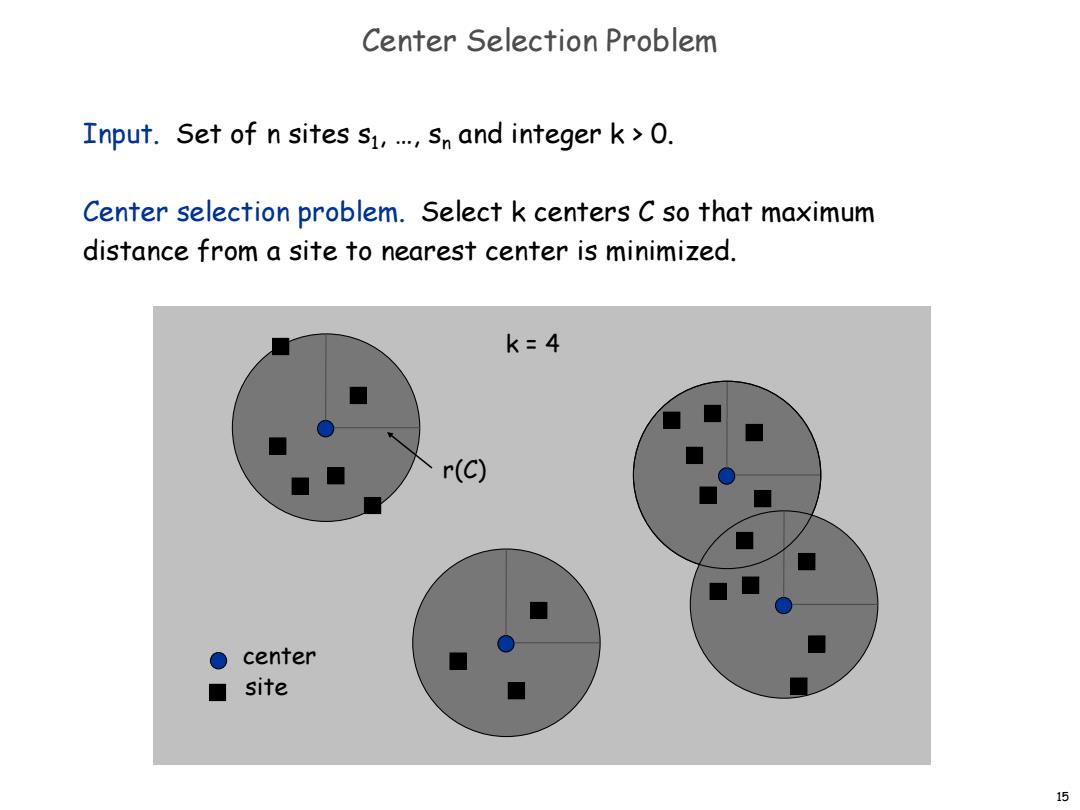
Center Selection Problem Input.Set of n sites s1,.sn and integer k>O. Center selection problem.Select k centers C so that maximum distance from a site to nearest center is minimized. k=4 r(C) O center ■ site 15
15 center r(C) Center Selection Problem Input. Set of n sites s1 , …, sn and integer k > 0. Center selection problem. Select k centers C so that maximum distance from a site to nearest center is minimized. site k = 4