
Load Balancing:List Scheduling Analysis Theorem.[Graham,1966]Greedy algorithm is a 2-approximation. First worst-case analysis of an approximation algorithm. Need to compare resulting solution with optimal makespan L*. Lemma 1.The optimal makespan L*maxj tj. Pf.Some machine must process the most time-consuming job. Lemma2.The optimal makespan L*≥a∑,t,: Pf. The total processing time is >jtj. One of m machines must do at least a 1/m fraction of total work. 6
6 Load Balancing: List Scheduling Analysis Theorem. [Graham, 1966] Greedy algorithm is a 2-approximation. First worst-case analysis of an approximation algorithm. Need to compare resulting solution with optimal makespan L*. Lemma 1. The optimal makespan L* maxj tj . Pf. Some machine must process the most time-consuming job. ▪ Lemma 2. The optimal makespan Pf. The total processing time is j tj . One of m machines must do at least a 1/m fraction of total work. ▪ L * 1 m t j j
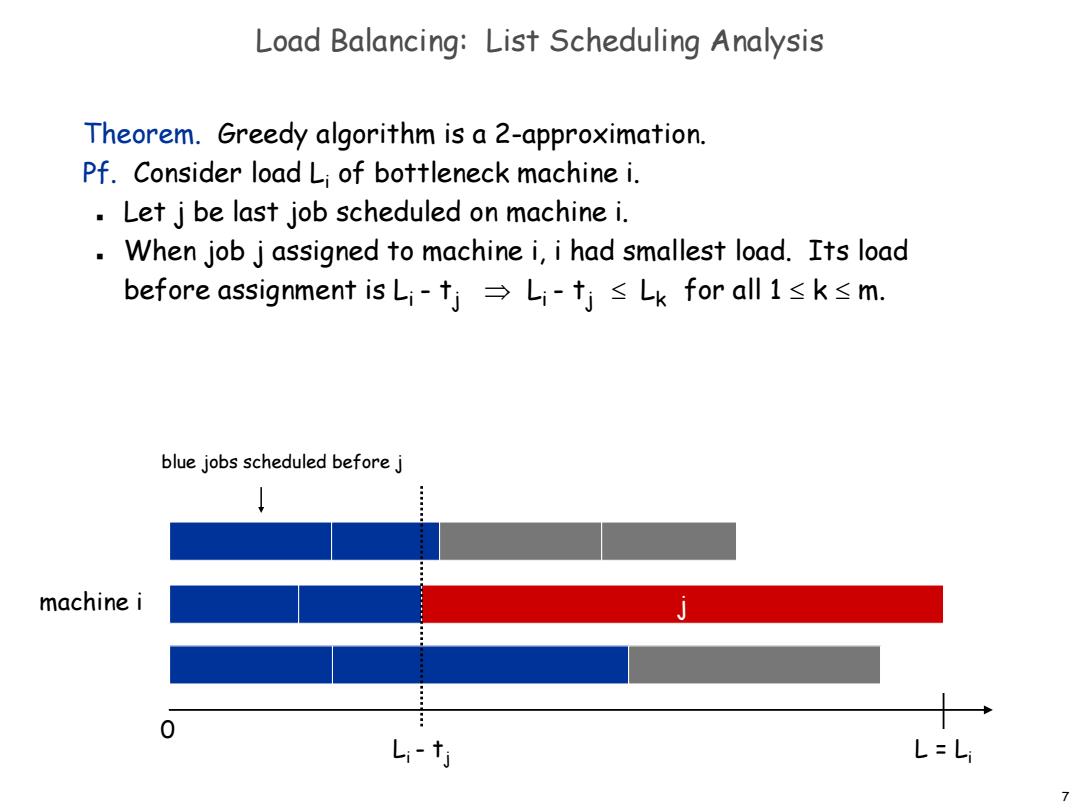
Load Balancing:List Scheduling Analysis Theorem.Greedy algorithm is a 2-approximation. Pf.Consider load Li of bottleneck machine i. Let j be last job scheduled on machine i. When job j assigned to machine i,i had smallest load.Its load before assignment is Li-tj→Li-tj≤Lk for all1≤k≤m. blue jobs scheduled before j machine i Li-tj L=L: 7
7 Load Balancing: List Scheduling Analysis Theorem. Greedy algorithm is a 2-approximation. Pf. Consider load Li of bottleneck machine i. Let j be last job scheduled on machine i. When job j assigned to machine i, i had smallest load. Its load before assignment is Li - tj Li - tj Lk for all 1 k m. j 0 Li L = Li - tj machine i blue jobs scheduled before j

Load Balancing:List Scheduling Analysis Theorem.Greedy algorithm is a 2-approximation. Pf.Consider load Li of bottleneck machine i. Let j be last job scheduled on machine i. When job j assigned to machine i,i had smallest load.Its load before assignment is Li-tj→Li-tj≤Lk for all1≤k≤m. Sum inegualities over all k and divide by m: L,-4≤a∑kL h∑k Lemma 1 ≤L* ·NowL;=(L,-4)+t) ≤2L*. ≤L* ≤L米 1 Lemma 2 8
8 Load Balancing: List Scheduling Analysis Theorem. Greedy algorithm is a 2-approximation. Pf. Consider load Li of bottleneck machine i. Let j be last job scheduled on machine i. When job j assigned to machine i, i had smallest load. Its load before assignment is Li - tj Li - tj Lk for all 1 k m. Sum inequalities over all k and divide by m: Now ▪ Li t j 1 m k Lk 1 m t k k L * Li (Li t j ) L* t j L* 2L *. Lemma 2 Lemma 1
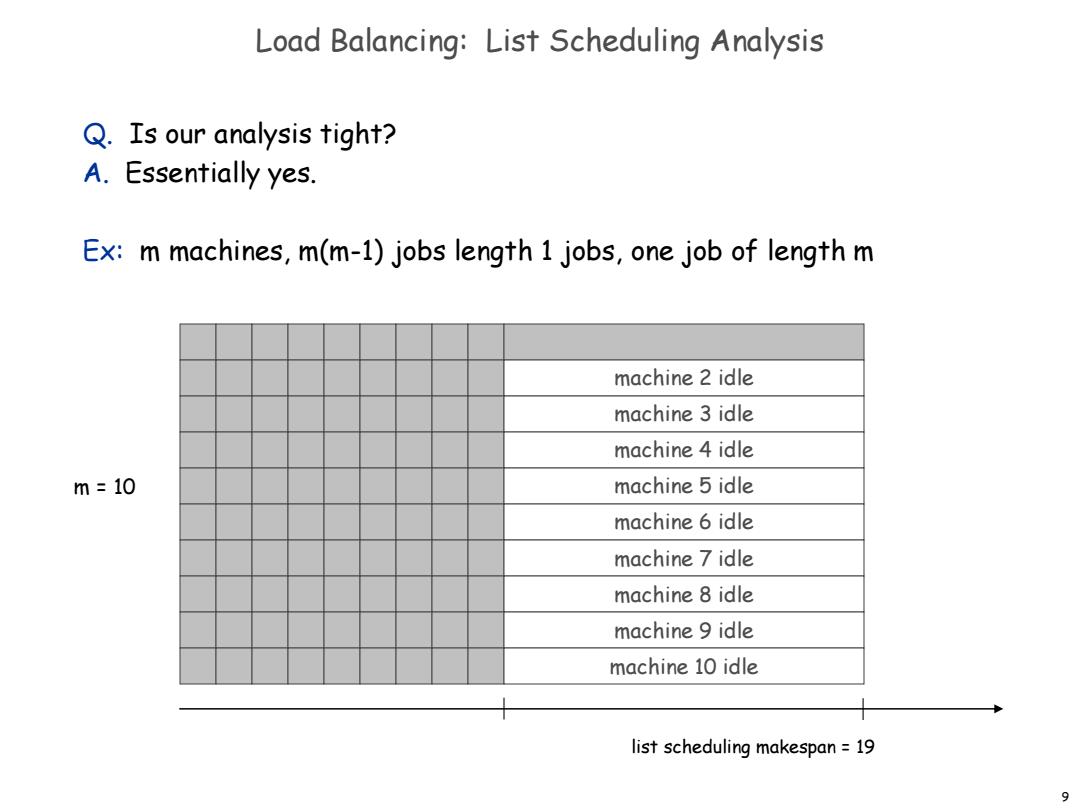
Load Balancing:List Scheduling Analysis Q.Is our analysis tight? A.Essentially yes. Ex:m machines,m(m-1)jobs length 1 jobs,one job of length m machine 2 idle machine 3 idle machine 4 idle m=10 machine 5 idle machine 6 idle machine 7 idle machine 8 idle machine 9 idle machine 10 idle list scheduling makespan 19 9
9 Load Balancing: List Scheduling Analysis Q. Is our analysis tight? A. Essentially yes. Ex: m machines, m(m-1) jobs length 1 jobs, one job of length m machine 2 idle machine 3 idle machine 4 idle machine 5 idle machine 6 idle machine 7 idle machine 8 idle machine 9 idle machine 10 idle list scheduling makespan = 19 m = 10
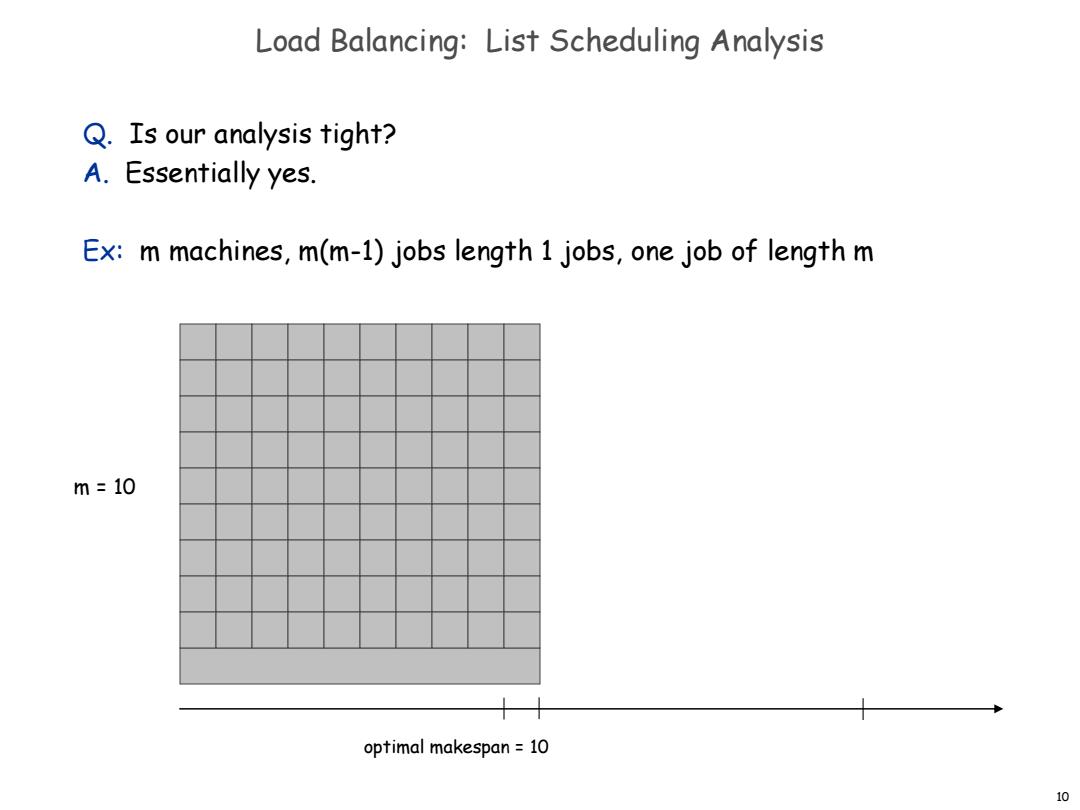
Load Balancing:List Scheduling Analysis Q.Is our analysis tight? A.Essentially yes. Ex:m machines,m(m-1)jobs length 1 jobs,one job of length m m=10 optimal makespan 10 10
10 Load Balancing: List Scheduling Analysis Q. Is our analysis tight? A. Essentially yes. Ex: m machines, m(m-1) jobs length 1 jobs, one job of length m m = 10 optimal makespan = 10