
Center Selection Problem Input.Set of n sites s1,..,sn and integer k>O. Center selection problem.Select k centers C so that maximum distance from a site to nearest center is minimized. Notation. dist(x,y)=distance between x and y. dist(si,C)=mincec dist(si,c)=distance from s;to closest center. r(C)=maxi dist(si,C)=smallest covering radius. Goal.Find set of centers C that minimizes r(C),subject to |Cl=k. Distance function properties. dist(x,x)=O (identity) dist(x,y)=dist(y,x) (symmetry) ·dist(x,y)≤dist(x,z)+dist(z,y) (triangle inequality) 16
16 Center Selection Problem Input. Set of n sites s1 , …, sn and integer k > 0. Center selection problem. Select k centers C so that maximum distance from a site to nearest center is minimized. Notation. dist(x, y) = distance between x and y. dist(si , C) = min c C dist(si , c) = distance from si to closest center. r(C) = maxi dist(si , C) = smallest covering radius. Goal. Find set of centers C that minimizes r(C), subject to |C| = k. Distance function properties. dist(x, x) = 0 (identity) dist(x, y) = dist(y, x) (symmetry) dist(x, y) dist(x, z) + dist(z, y) (triangle inequality)
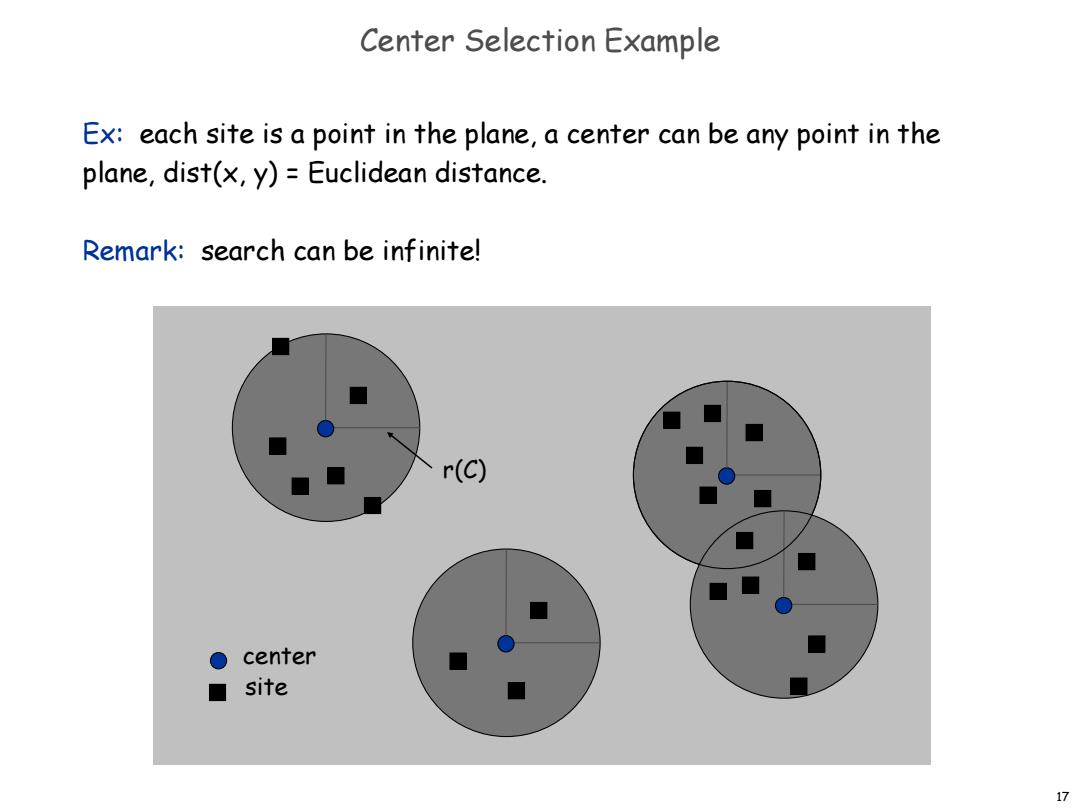
Center Selection Example Ex:each site is a point in the plane,a center can be any point in the plane,dist(x,y)=Euclidean distance. Remark:search can be infinite! r(C) O center ■ site 17
17 center site Center Selection Example Ex: each site is a point in the plane, a center can be any point in the plane, dist(x, y) = Euclidean distance. Remark: search can be infinite! r(C)

Greedy Algorithm:A False Start Greedy algorithm.Put the first center at the best possible location for a single center,and then keep adding centers so as to reduce the covering radius each time by as much as possible. Remark:arbitrarily bad! ● greedy center 1 ●center k=2 centers ■site 18
18 Greedy Algorithm: A False Start Greedy algorithm. Put the first center at the best possible location for a single center, and then keep adding centers so as to reduce the covering radius each time by as much as possible. Remark: arbitrarily bad! greedy center 1 k = 2 centers site center

Center Selection:Greedy Algorithm Greedy algorithm.Repeatedly choose the next center to be the site farthest from any existing center. Greedy-Center-Selection (k,n,s1,s2,...,s){ C=φ repeat k times Select a site s;with maximum dist(s;,C) Add s;to C ] site farthest from any center return C Observation.Upon termination all centers in C are pairwise at least r(C) apart. Pf.By construction of algorithm. 9
19 Center Selection: Greedy Algorithm Greedy algorithm. Repeatedly choose the next center to be the site farthest from any existing center. Observation. Upon termination all centers in C are pairwise at least r(C) apart. Pf. By construction of algorithm. Greedy-Center-Selection(k, n, s1,s2,…,sn) { C = repeat k times { Select a site si with maximum dist(si, C) Add si to C } return C } site farthest from any center

Center Selection:Analysis of Greedy Algorithm Theorem.Let C*be an optimal set of centers.Then r(C)<2r(C*). Pf.(by contradiction)Assume r(C*)<r(C). For each site ci in C,consider ball of radiusr(C)around it. Exactly one c*in each ball;let ci be the site paired with c*. Consider any site s and its closest center c*in C*. ·dist(s,C)≤dist(s,c)≤dist(s,c*)+dist(c*,c)≤2r(C*) .Thus r(C)≤2r(C*).·\, 人 △-inequality s r(C*)since c*is closest center 是r(C) r(C) Ci 是r(C) ●C* ■sites C* 20
20 Center Selection: Analysis of Greedy Algorithm Theorem. Let C* be an optimal set of centers. Then r(C) 2r(C*). Pf. (by contradiction) Assume r(C*) < ½ r(C). For each site ci in C, consider ball of radius ½ r(C) around it. Exactly one ci* in each ball; let ci be the site paired with ci*. Consider any site s and its closest center ci* in C*. dist(s, C) dist(s, ci ) dist(s, ci*) + dist(ci*, ci ) 2r(C*). Thus r(C) 2r(C*). ▪ C* sites ½ r(C) ci ci * s r(C*) since ci* is closest center ½ r(C) ½ r(C) -inequality