
§6-1粒子体系镜计分布的基本知识 2 独立粒子体系和相依粒子体系 独立粒子体系 粒子之间的相互作用非常弱,在理论处理时可以忽 略不计,因此也叫近独立粒子体系,如理想气体和 低压气体。体系的总能量为各个粒子能量之和。 U=n1e1+n282+.+nk=∑n:e 上页 下页 回主目录 返回 2024年9月5日
2024年9月5日 2. 独立粒子体系和相依粒子体系 独立粒子体系 粒子之间的相互作用非常弱,在理论处理时可以忽 略不计,因此也叫近独立粒子体系,如理想气体和 低压气体。体系的总能量为各个粒子能量之和。 U = n1 ε1 + n2 ε2 +.+ nk εk = Σni εi §6-1 粒子体系统计分布的基本知识

§6-1粒子体素镜计分布的基本知积 相依粒子体系 粒子之间的相互作用较大,理论处理时不能忽略, 因此也称非独立粒子体系,如高压气体和液体等。体 系的总能量除了各个粒子的能量之和外,还包括粒子 之间相互作用形成的势能。 U=2n8+U势 这种势能是各个粒子空间位置的函数。 本章讨论独立粒子体系 上页 下页 回主目录 返国 2024年9月5日
2024年9月5日 相依粒子体系 粒子之间的相互作用较大,理论处理时不能忽略, 因此也称非独立粒子体系,如高压气体和液体等。体 系的总能量除了各个粒子的能量之和外,还包括粒子 之间相互作用形成的势能。 U = Σni εi + U势 这种势能是各个粒子空间位置的函数。 本章讨论独立粒子体系 §6-1 粒子体系统计分布的基本知识

§6-2麦克斯威-波尔兹曼统计 一,N、以均为定值的独立、可别粒子体系 任一分布所具有的微观状态数: 分布状况: n n2 nk E 2 e k Φ2 k 由(6-6)式,此分布所含微观状态数为: N 上页 下页 回 主目录 返回 2024年9月5日
2024年9月5日 §6-2 麦克斯威-波尔兹曼统计 一.N、U、V均为定值的独立、可别粒子体系 任一分布所具有的微观状态数: 分布状况: n1 n2 . nk ε1 ε2 . εk φ1 φ2 . φk 由(6-6)式,此分布所含微观状态数为: = i i j n N t ! !
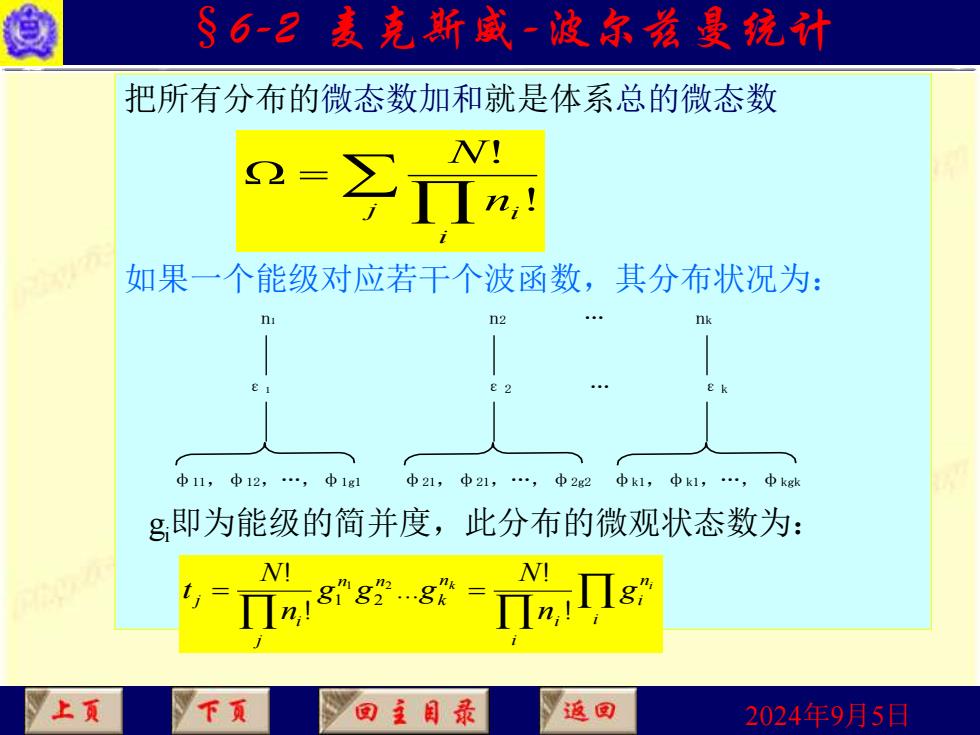
§6-2麦克斯威-波尔羞曼统计 把所有分布的微态数加和就是体系总的微态数 2->I N! 1n, 如果一个能级对应若干个波函数,其分布状况为: n n2 nk e2 中11,中12,φ1g1 中21,中21,.,中2g2 中k1,中k1,.,中kgk g即为能级的简并度,此分布的微观状态数为: N! n1883.8 上页 下页 回主目录 返回 2024年9月5日
2024年9月5日 把所有分布的微态数加和就是体系总的微态数 gi即为能级的简并度,此分布的微观状态数为: = j i ni N ! ! 如果一个能级对应若干个波函数,其分布状况为: φ11,φ12,.,φ1g1 φ21,φ21,.,φ2g2 φk1,φk1,.,φkgk ε1 ε2 . εk n1 n2 . nk = = i n i i i n k n n j i j k i g n N g g g n N t ! ! . ! ! 1 2 1 2 §6-2 麦克斯威-波尔兹曼统计

§6-2麦克斯威-波尔兹曼统计 体系所有分布的微态数为: Q-> aΠ”=空网 二最可几分布的微观状态数 此为在2n=N和2n,e,=U为定值的两个条件 下求分布的微态数具有最大值的问题,在数学上即为 求解条件极值的问题 由于: nt=lnN-∑nn, 根据斯特令公式 In N!-NIn N-N 可得到 lnt=NnN-∑n,hn, 上页 下页 回 主目录 返回 2024年9月5日
2024年9月5日 体系所有分布的微态数为: 此为在 Σni = N 和 Σni ei = U 为定值的两个条件 下求分布的微态数具有最大值的问题,在数学上即为 求解条件极值的问题 = = j i i n i j i n i i i n g g N n N i i ! ! ! ! 二 最可几分布的微观状态数 由于: = − i N ni ln t ln ! ln ! 根据斯特令公式 ln N!= Nln N − N 可得到 = − i N N ni ni ln t ln ln §6-2 麦克斯威-波尔兹曼统计