4-4力矩的功刚体绕定轴转动的动能定理 第四章刚体的转动 力的空间累积效应力的功,动能,动能定理. 力矩的空间累积效应力矩的功,转动动能,动能定理 、力矩作功 dw=F.dr=Fds do Frd0 dw=Mdo 力矩的功 w- Mde dw do 力矩的功率 Ps =M =M0 dt dt
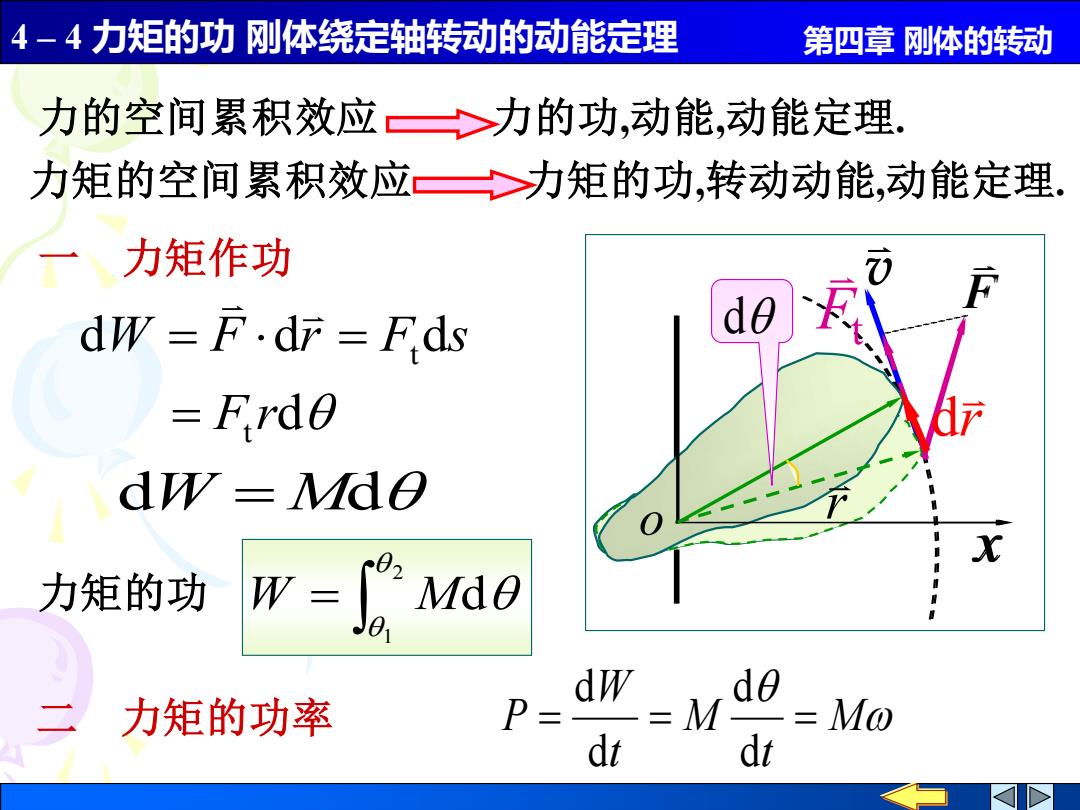
4 – 4 力矩的功 刚体绕定轴转动的动能定理 第四章 刚体的转动 d d d d t t F r W F r F s = = = dW = Md = 2 1 d 力矩的功 W M 一 力矩作功 力的空间累积效应 力的功,动能,动能定理. 力矩的空间累积效应 力矩的功,转动动能,动能定理. M t M t W P = = = d d d d 二 力矩的功率 o r v F x v F o x r Ft r d d

4-4力矩的功刚体绕定轴转动的动能定理 第四章刚体的转动 三 转动动能 B-∑am=∑auro-w 四刚体绕定轴转动的动能定理 p=6=Jd8=ada w-0-22 合外力矩对绕定轴转动的刚体所作的功等于刚体 转动动能的增量
4 – 4 力矩的功 刚体绕定轴转动的动能定理 第四章 刚体的转动 2 1 2 2 2 1 2 1 d 2 1 W = M = J − J 三 转动动能 2 2 1 i i i Ek = m v 四 刚体绕定轴转动的动能定理 = 2 1 d W M 合外力矩对绕定轴转动的刚体所作的功等于刚体 转动动能的增量 . 2 2 2 2 1 ( ) 2 1 mi ri J i = = = = 2 1 1 1 d d d d J t J
4-4力矩的功刚体绕定轴转动的动能定理 第四章刚体的转动 讨论 子细 子弹击入杆 圆锥摆 袋计 以子弹和沙袋为系统! 以子弹和杆为系统 圆锥摆系统 动量守恒; 动量不守恒; 动量不守恒; 角动量守恒; 角动量守恒; 角动量守恒; 机械能不守恒. 机械能不守恒. 机械能守恒
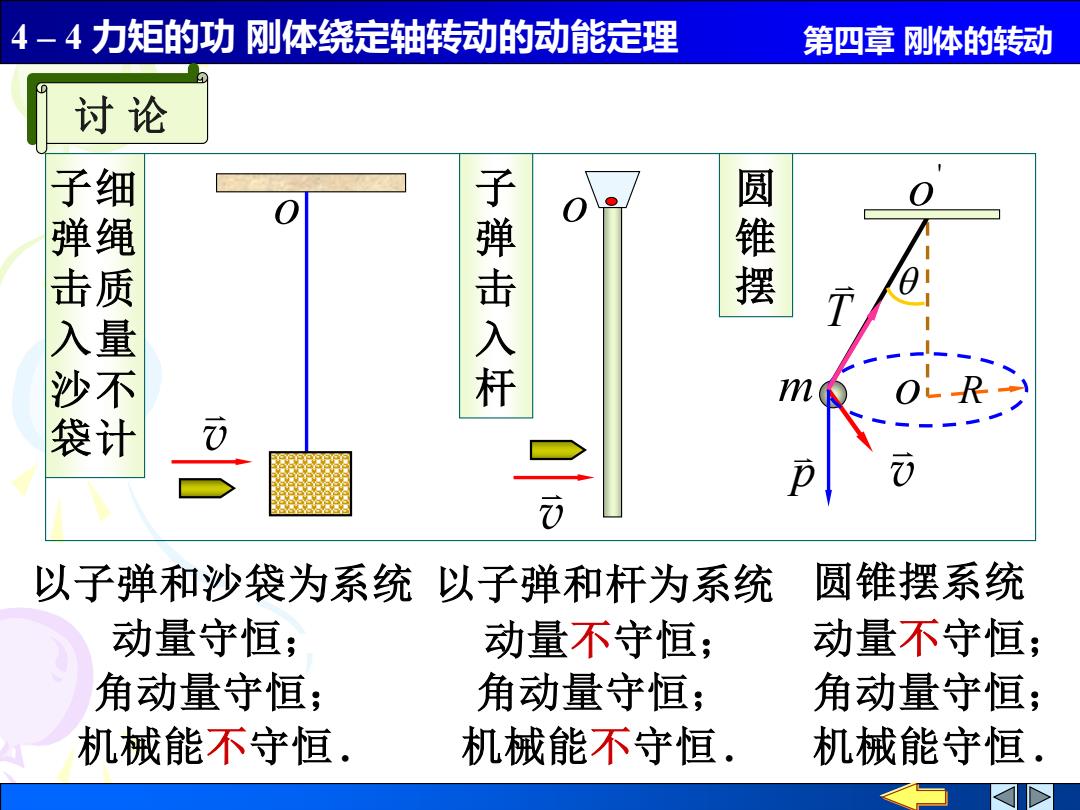
4 – 4 力矩的功 刚体绕定轴转动的动能定理 第四章 刚体的转动 v o v o ' o m p T R 圆 锥 摆 子 弹 击 入 杆 o v 以子弹和杆为系统 机械能不守恒 . 角动量守恒; 动量不守恒; 以子弹和沙袋为系统 动量守恒; 角动量守恒; 机械能不守恒 . 圆锥摆系统 动量不守恒; 角动量守恒; 机械能守恒 . 讨 论 子 弹 击 入 沙 袋 细 绳 质 量 不 计

4-4力矩的功刚体绕定轴转动的动能定理 第四章刚体的转动 例1一质量为m、半径为R的圆盘,可绕一垂 直通过盘心的无摩擦的水平轴转动.圆盘上绕有轻绳, 一端挂质量为m的物体.问物体在静止下落高度h时, 其速度的大小为多少?设绳的质量忽略不计 解拉力F对圆盘做功,由刚体绕定轴转动的动 能定理可得,拉力F的力矩所作的功为 FRde-R["F do 1 m 0,0和0、0分别 为圆盘终了和起始时的角 坐标和角速度
4 – 4 力矩的功 刚体绕定轴转动的动能定理 第四章 刚体的转动 o R h m' m m 2 0 2 2 1 2 1 = J − J 和 、 分别 为圆盘终了和起始时的角 坐标和角速度 . 0 , 0 d d 0 0 FT R = R FT 例1 一质量为 、半径为 R 的圆盘,可绕一垂 直通过盘心的无摩擦的水平轴转动 . 圆盘上绕有轻绳, 一端挂质量为m 的物体 . 问物体在静止下落高度 h 时, 其速度的大小为多少? 设绳的质量忽略不计 . m' 解 拉力 对圆盘做功,由刚体绕定轴转动的动 能定理可得,拉力 的力矩所作的功为 FT FT o FT FN P' FT P m

4-4力矩的功刚体绕定轴转动的动能定理 第四章刚体的转动 FRdO-RI FdO- 2 由质点动能定理 - D meh-Rrd0-号m 物体由静止开始下落V0=0,⊙,=0 p 并考虑到圆盘的转动惯量J= )=0R 解得 mgh n 2gh m'+2m V(m'/2)+m
4 – 4 力矩的功 刚体绕定轴转动的动能定理 第四章 刚体的转动 2 0 2 T T 2 1 2 1 d d 0 0 F R = R F = J − J 物体由静止开始下落 v0 = 0,0 = 0 解得 gh m 2 ( ' 2) m m m 2m mgh v 2 + = + = 并考虑到圆盘的转动惯量 2 2 1 J = m R 2 0 2 T 2 1 2 1 d 0 mgh− R F = mv − mv 由质点动能定理 FT FT = − o FT FN P' FT P m v =R