
解:过程图示如下 n5 mol n=5 mol ahat恤 n=5 mol 五-300K 1=300K p=200 kP p3=50 kPa P=200kPa 要确定了,只需对第二步应用绝热状态方程 ,对双原子气体 因此 16-1 由于理想气体的V和H只是温度的函数, △U=nCvm3-T)=5×5R/2445.8-300)=15.15kJ △H=nC,a-T)=5×7R/2)×(445.8-300)=21.21k 整个过程由于第二步为绝热,计算热是方便的。而第一步为恒温可逆 △1=0 Q-8=男-资=m合 =5x8314×30xh0-1729时 W=△0-2=15.15-17.29=-2.14k 2.25求证在理想气体广V图上任一点处,绝热可逆线的斜率的绝对值大于恒温可逆线的绝对值
解:过程图示如下 要确定 ,只需对第二步应用绝热状态方程 ,对双原子气体 因此 由于理想气体的 U 和 H 只是温度的函数, 整个过程由于第二步为绝热,计算热是方便的。而第一步为恒温可逆 2.25 求证在理想气体 p-V 图上任一点处,绝热可逆线的斜率的绝对值大于恒温可逆线的绝对值
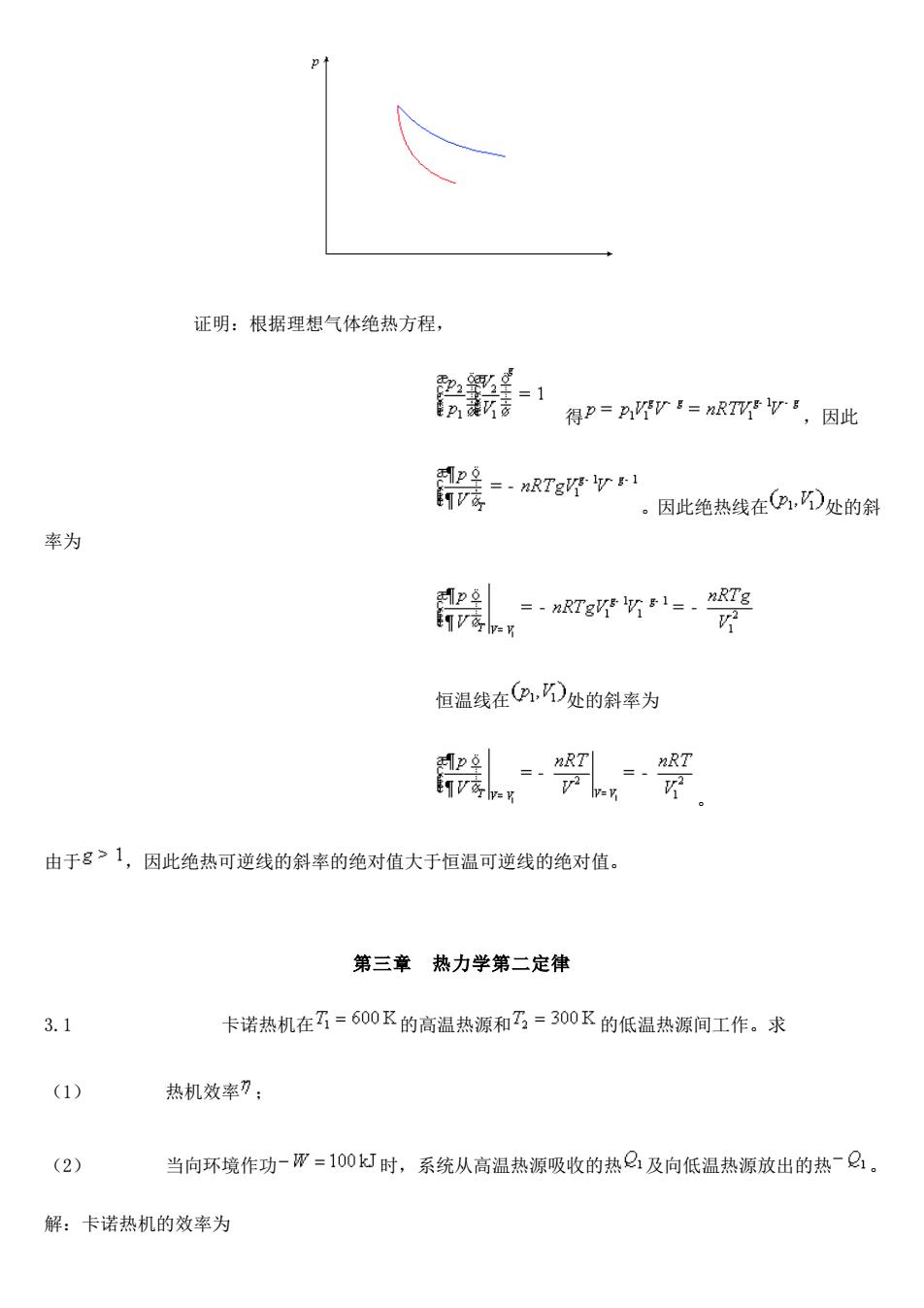
证明:根据理想气体绝热方程, 会群-1 得P=nr=RTV',因此 器=ar 。因此绝热线在,D处的斜 率为 ,野婴 恒温线在,D处的斜率为 , 由于8>1,因此绝热可逆线的斜率的绝对值大于恒温可逆线的绝对值。 第三章热力学第二定律 3.1 卡诺热机在了=600K的高温热源和乃,=300K的低温热源间工作。求 (1) 热机效率刀: (2) 当向环境作功-而=100k灯时,系统从高温热源吸收的热Q及向低温热源放出的热~Q。 解:卡诺热机的效率为
证明:根据理想气体绝热方程, 得 ,因此 。因此绝热线在 处的斜 率为 恒温线在 处的斜率为 。 由于 ,因此绝热可逆线的斜率的绝对值大于恒温可逆线的绝对值。 第三章 热力学第二定律 3.1 卡诺热机在 的高温热源和 的低温热源间工作。求 (1) 热机效率 ; (2) 当向环境作功 时,系统从高温热源吸收的热 及向低温热源放出的热 。 解:卡诺热机的效率为

7=1-21-需=50% 根据定义 2+g=-W:-2=2-(W)=200-100=100k 32 某地热水的温度为65℃,大气温度为20℃,若分别利用一可逆热机和一不可逆热机从地热水中取出1000J的热量, ()分别计算两热机对外所做功:已知不可逆热机效率是可逆热级效*的80%: (②分别计算两热机向大气放出的热。 解:高温热源为地热水:T=338.15Kg=1000】 低温热源为大气:了=293.15K 0%--五.3815-2935-013 338.15 所以用=07.=-1000×0.133J=-133J 7=0.87.=0.8×0.133=0.1065 P=-0=-1000×0.1065J=-106.5J 回由9-名8台是程28-” 所以2=-Q-W,=(133-1000)J=-867J 0=0-W=(106.5-1000)J=-893.5J 3.3 高温热源温度Z=600K,低温热源乃=300K。今有120k灯的热直接从高温热源传给低温 热源,求此过程的△S 解:将热源看作无限大,因此,传热过程对热源来说是可逆过程 =200J.K1 3.4 已知氮(心,g)的摩尔定压热容与温度的函数关系为 C,m=27.32+6.226×10-3(TK)-0.9502×10-TK月y:mo1-1.K- 将始态为300K,100kPa下1mol的(g)置于1000K的热源中,求下列过程 (1)经恒压过程:(2)经恒容过程达到平衡态时的2,△S及△S
根据定义 3.3 高温热源温度 ,低温热源 。今有 120 kJ 的热直接从高温热源传给低温 热源,求此过程的 。 解:将热源看作无限大,因此,传热过程对热源来说是可逆过程 3.4 已知氮(N2, g)的摩尔定压热容与温度的函数关系为 将始态为 300 K,100 kPa 下 1 mol 的 N2(g)置于 1000 K 的热源中,求下列过程 (1)经恒压过程;(2)经恒容过程达到平衡态时的

解:在恒压的情况下 As-aC-回sr=272h要+625x10*6-列 -09502×10G-T】 =36.82JK1 2=aC,.7=27.32g-Z+6226×10g-r】 2 0.9502x10-T) =21.65k △8=-2165x102-21651K 1000 △S。=△S+△S=3682-21.65=15.17J-K1 在恒容情况下,将氮(N2,g)看作理想气 CYn =Cya-R ={19.01+6.226×103T/K)-0.9502×10tR2:mo11.K1 将C,⑦)代替上面各式中的S,何)),即可求得所需各量 △S=26.81J.K1,Q=15.83k5:S=-15.83JK1: 6So=-10.98JK- 3.5 始态为乃=300K,P=200kPa的某双原子理想气体1mol,经下列不同途径变化 到3,=300K,P2=100a的末态.求各步骤及途径的2,△S。 (1) 恒温可逆膨胀: (2) 先恒容冷却至使压力降至100kPa,再恒压加热至T: (3) 先绝热可逆膨胀到使压力降至100kPa,再恒压加热至。 解:(1)对理想气体恒温可逆膨胀,V=0,因此
解:在恒压的情况下 在 恒 容 情 况 下 , 将 氮 ( N2, g ) 看 作 理 想 气 体 将 代替上面各式中的 ,即可求得所需各量 3.5 始态为 , 的某双原子理想气体 1 mol,经下列不同途径变化 到 , 的末态。求各步骤及途径的 。 (1) 恒温可逆膨胀; (2) 先恒容冷却至使压力降至 100 kPa,再恒压加热至 ; (3) 先绝热可逆膨胀到使压力降至 100 kPa,再恒压加热至 。 解:(1)对理想气体恒温可逆膨胀, U = 0,因此

1a0-18 =5.763J.K (2) 先计算恒容冷却至使压力降至100kPa,系统的温度 20150K g=G.r-小-1×登00-0则-31i8 △=Cah会=-141g e,-c.G-小1x7受60-15到-4365 △S,=C,ah2=20.170JK 2=Q+02=7.483kJ △S=△S1+△S2=5.76JK (3) 同理,先绝热可逆膨胀到使压力降至100kPa时系统的温度T: 根据理想气体绝热过程状态方程, -6- 7=2 100)2 P =300×200】 =246.1K 各热力学量计算如下 Q=0,S1=0 g,=,=8C,nG-T-7x600-2461)=1568w 2-登器wx 2=02=1.568k5,△S=4S2=5.763J.K- 3.61mol理想气体在T=300K下,从始态100P阳经历下列过程达到各自的平衡态。求各过程的Q、△ S、△Sio。 (1)可逆膨胀至末态压力50kPa: (2)反抗恒定外压50kPa不可逆膨胀至平衡态:
(2) 先计算恒容冷却至使压力降至 100 kPa,系统的温度 T: (3) 同理,先绝热可逆膨胀到使压力降至 100 kPa 时系统的温度 T: 根据理想气体绝热过程状态方程, 各热力学量计算如下 3.6 1mol 理想气体在 T=300K 下,从始态 100kPa 经历下列过程达到各自的平衡态。求各过程的 Q、△ S、△Siso。 (1)可逆膨胀至末态压力 50kPa; (2)反抗恒定外压 50kPa 不可逆膨胀至平衡态;