
解:由附录查得25℃时 AH (CH;COOH,g)=-432.25 kJ.mol-1 AHe (CH,g)=-74.81 kJ.mol-1 △H8(C02,g)=-393.509kmol1 4H品(298.15K)=4H(CH,g+4H(CO2,g)-4HR(CH000H,g =-(74.81+393.509-432.25)kJ.mol1 =-36.069kmol1 对于题给反应, ACp.m=>vBCp.m(B,B) =Cp.m(CH,g)+Cp.m(CO2,g)-Cp.m(CH,COOH,g) =(37.7+31.4-52.3小K-1mol1 =16.8Jmol1.K-1 T=1000K时题给反应的标准摩尔反应焓 AH(T)=AH(T)+A.C.ndT T1 =△H(T)+△C.m(T-T) =-36.069 kJ.mol-1+16.18×(1000-298.15)×10-3 kJ'mol1 =-24.28 kJ'mol1 2.21 甲烷与过量50%的空气混合,为使恒压燃烧的最高温度能达到2000℃,求燃烧前混合气体应 预热到多少摄氏度。物资的标准摩尔生成培数据见附录。空气组成按0,=0.21,,8)=0.79计 算。各物资的平均摩尔定压热容,力:m01K分别为:CH,g)7531,O,g)3347,,g)3347 C02g)54.39.H0g4184 解:燃烧为恒压绝热过程。化学反应式CH,(g)+20,g)=C0,g)+2H,0g) 设计途径如下
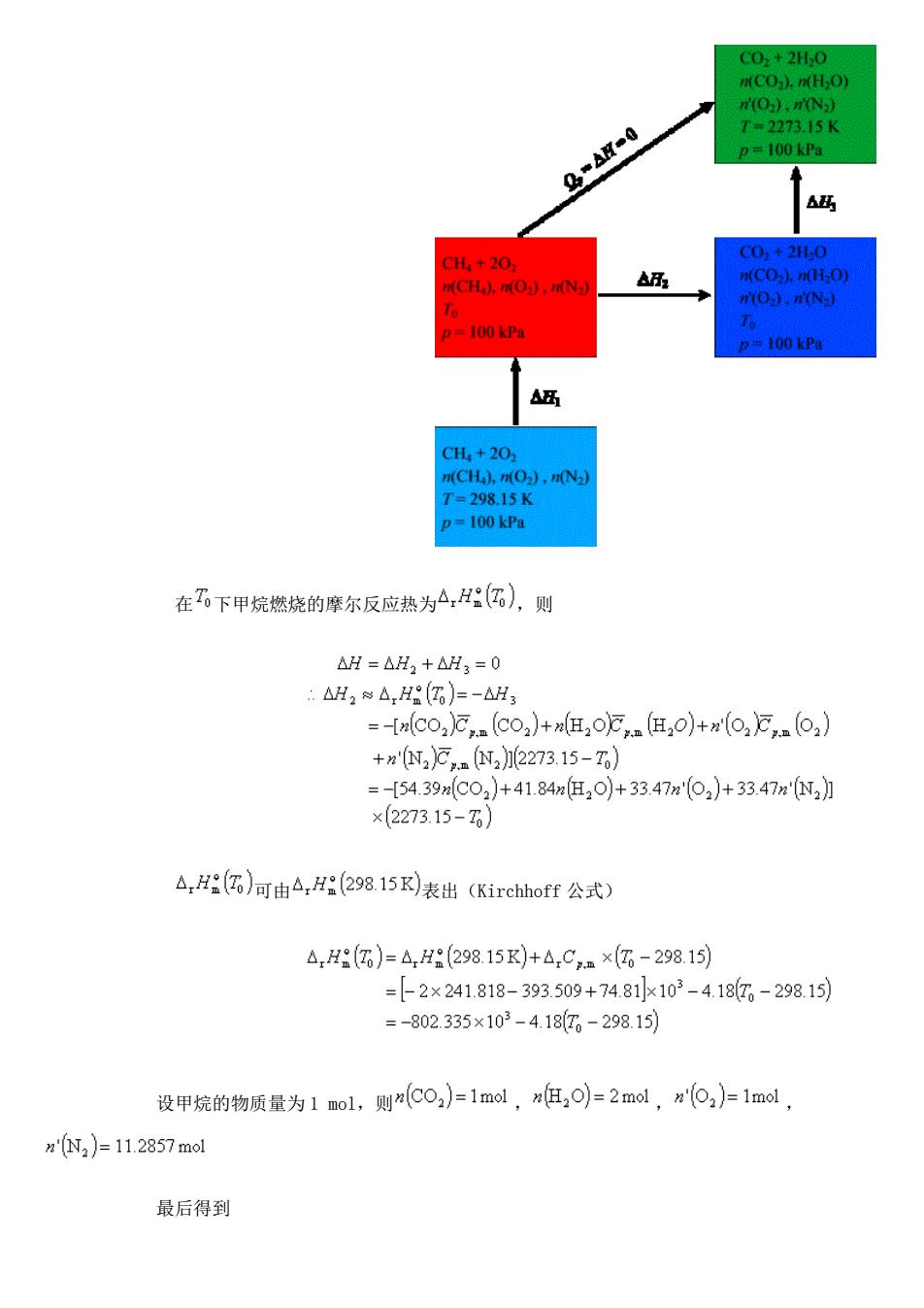
2.21 甲烷与过量 50%的空气混合,为使恒压燃烧的最高温度能达到 2000℃,求燃烧前混合气体应 预热到多少摄氏度。物资的标准摩尔生成焓数据见附录。空气组成按 , 计 算。各物资的平均摩尔定压热容 分别为: ; ; ; ; 。 解:燃烧为恒压绝热过程。化学反应式 设计途径如下
C02+2H0 m(CO]).n(H-O) 0),nN2 7=227315K 2=100k 码 0+2 00 0), 0).0 =100 kPa =100kPa 五 CH+20 m(CH),n(O2),n(N2 7=29815K =100kPa 在下甲烷燃烧的摩尔反应热为A,HG),则 △H=△H2+△H3=0 :△H2sA,H(G6)=-AH3 ={nlco,E,.co2)+n,o万,nH,0)+x(o2E,.o2】 +n'2),.(22273.15-I) =-54.39x(C02)+41.84x但20)+33.47m'(02)+33.47mN2】 ×(2273.15-0】 △,HG)可由4,H298.15K表出(Kirchhoff公式) △,H()=4H(298.15K)+△,C,m×(-298.15) =2×241.818-393.509+74.81×103-4.180,-298.15) =-802.335×103-4.187-298.15) 设甲烷的物质量为1mol,则m(C0,)=1mol,n但,o)=2mol,为'o,)=1ml, n'N2)=11.2857mol 最后得到
在 下甲烷燃烧的摩尔反应热为 ,则 可由 表出(Kirchhoff 公式) 设甲烷的物质量为 1 mol,则 , , , 最后得到

-802.335×103-4.187。-298.15)=-549.27242273.15-T) 6=80854K=535.4°C 2.22 氢气与过量50%的空气混合物置于密闭恒容的容器中,始态温度为 25℃,压力为100kPa。 将氢气点燃,反应瞬间完成后,求系统所能达到的最高温度和最大压力。 空气的组成按y(O2)=0.21,y(以)=0.79计算。水蒸气的标准摩尔生成焓见 教材附录,各气体的定容摩尔热容分别为:Cv,m(O2)=Cv.m(5)=25.1小md1. K.Cv.m(H2O,g)=37.66J小md.K。假设气体适用理想气体状态方程。 解:在体积恒定的容器中发生燃烧反应,瞬间完成,常发生爆炸,求爆炸反 应在理论上可能达到的最高温度和最大压力应按绝热恒容计算。由反应H2+ 20,一,0(g)可知,每燃烧1ml的,(g),在理论上需要0.5mol的0,(g)。 今以1m0lH2(g)为计算基准,O2(g)过量50%,所需O2(g)的物质的量 n(02)=0.5(1+50%)mol=0.75mol1 同时必然引人2(g),n(N2)=0.75mol×7921=2.8214mol。可通过下列过 程来计算反应可能达到的最高温度和最大压力 h+0.750+2.214N0h0g+0.250+2.214地 t1=25℃,p1=100kPa t,p 2)1 →Hh0(g)+0.2502+2.82142 t1=25℃ 解法1:题给过程为Q=0,dV=0,W'=0,可由△U=△U1+△U2=0来 计算末态的温度。由附录查得: △H(H20,g,298.15K)=-241.818 kJ.mol-1 过程(1)为恒容恒温反应过程: △H1=n(HhzO,g)△H(H2O,g,298.15K) =-241.818kmol1×1mol
2.22

=-241.818k △n(g)=-0.5mol △U1=△H1-△n(g)RTi =-241.818+0.5×8.3145×298.15×10-3kJ =-240.579kJ 过程(2)为反应产物的恒容升温过程: △U2=2nBCv,m(B,产物)(t-t1) =In(HO,g)Cv.m(H2O,g)+n(O)Cv.m(O)+n(N2)Cv.m(N2)I(t-t1) =(37.66+0.25×25.1+2.8214×25.1)(t℃-25)J =114.752×(t/℃-25)×10-3kJ △U=△U1+△U2=-240.579kJ+114.752×(t/℃-25)×10-3k=0 由上式可得最高温度 240.579 t=(114.752×10+25)℃=2121.5t 2nB(反应物,g)=n1(O2)+n(N2)+n(H2) =(0.75+2.8214+1)mol =4.5714mol nB(产物,g)=n2(O2)+n()+n(HO,g) =4.0714mol 因为p1V=∑nB(反应物,g)RT1,pV=∑nB(产物,g)RT s(产物.g)T 所以设物27×=49器×10 =715.3kPa 解法2:末态温度也可由AH来计算。 前已求出:△H1=-241.818k △,(pV)=∑nB(产物,g)RT-∑nB(反应物,g)RT1 =(4.0714×8.3145T/K-4.5714×8.3145×298.15)J =(33.852T/K-11332.36)×10-3k 因为△U=0 所以△,H=△,U+△.(V)=△,(pV)=△H1+△H2 AH2 =In(H2O,g)Cp.m(H2O)+n2(Oz)Cp.m(O2)+ n(N2)Cp.m(N2)(T-Ti) ={(37.66+8.3145)+(2.8214+0.25)×(25.1+ 8.3145)1(T/K-298.15J =148.604×(TK-298.15)J

△,H=△H1+△H2={-241.818×103+148.604×(T/K-298.15)J =△,(pV)=(33.852T/K-11332.36)J 由上式可得末态温度 T=241.818×103+148,604×29815-1132.36K 148.604-33.852 =2394.65K(即t=2121.5℃) 2.23某双原子理想气体1mo1从始态350K,200kPa经过如下五个不同过程达到各自的平衡态,求各过程 的功W。 (1) 恒温下可逆膨胀到50kPa: (2) 恒温反抗50kPa恒外压不可逆膨胀: (3) 绝热可逆膨胀到50kPa: (4) 绝热反抗50kPa恒外压不可逆膨胀 (5)恒温向真空膨胀到50kPa 解:双原子理想气体 n=5mol; Cv.m=(52)RCpm=(72)R )(T1=350RP1=200kPa)包aes&(I2=T1,卫2=50kPa) WmRT1h是-4034灯 2)(T1=350K,P1=200kPa)→(五2=T,P2=50kPa) W--P-,V--P,(V,-V;(-nRT,+nRT)--2183k 3)(T1=350K,P1=200kPa) 也张)(T2=?,B2=50kPa到 由绝热过程方程得 ×T=235.54R 绝热过程Q=0,Wr,a=△U=nCm△T=-2.379k 4)(①1=350KP1=200kPa)不5E)(T2=?,B2=50kPa 过程绝热Q=0,W=△U -pab△V=nCvm△T解得T2=275R .'W=AU=Cvn AT =-1.559kJ 5)W=0k灯 2.245mol双原子气体从始态300K,200kPa,先恒温可逆膨胀到压力为50kPa,在绝热可逆压缩到 未态压力200kPa。求末态温度7及整个过程的2,P,△0及△H
2.23 某双原子理想气体 1mol 从始态 350K,200kPa 经过如下五个不同过程达到各自的平衡态,求各过程 的功 W。 (1) 恒温下可逆膨胀到 50kPa; (2) 恒温反抗 50kPa 恒外压不可逆膨胀; (3) 绝热可逆膨胀到 50kPa; (4) 绝热反抗 50kPa 恒外压不可逆膨胀。 (5) 恒温向真空膨胀到 50kPa 解: 双原子理想气体 n = 5mol; CV,m =( 5/2)R ; Cp,m = (7/2)R 5) W=0 kJ 2.24 5 mol 双原子气体从始态 300 K,200 kPa,先恒温可逆膨胀到压力为 50 kPa,在绝热可逆压缩到 末态压力 200 kPa。求末态温度 T 及整个过程的 及