电子科技大学：《导波场论 Field Theory of Guided Waves》课程教学资源（课件讲稿）第二章 规则波导理论（2/5）

22用位丞数法求解波导中的场 2i+21.-0 E=K2 TI.+V(V.1.)e H=jogeiOVxII 口这三个方程适用于波导中任何电滋波型，也适用 于任何坐标系，但这组方程特别便于求解TM波。 口TM波，滋场无纵向分量，因此对于TM波，我们 取赫兹电矢量只有纵向分量。 I,=e.Ie 1.（p,9,2) 为什么？ 导波场论 6

2.2用位函数法求解波导中的场 p 这三个方程适用于波导中任何电磁波型，也适用 于任何坐标系，但这组方程特别便于求解TM波。 导波场论 2 ( ) j t e e E k e             j t e H j e       2 2 0 e e   k     p TM波，磁场无纵向分量，因此对于TM波，我们 取赫兹电矢量只有纵向分量。 e z ez   e     , ,  ez  p q z 为什么？ 6

2.2用位函数法求解波导中的扬 E=k211.+V(V.I1.)etw H=jogeoVxI 口假如赫兹电矢量有横向分量 H=joce(V,+V.)x(+) =joce(,xi)+(.×i.+v,×n) 口纵向分量 口横向分量 口如果赫兹电矢量有横向分量，其必然不是TM波 导波场论 7

2.2用位函数法求解波导中的场 2 ( ) j t e e E k e             j t e H j e       p 假如赫兹电矢量有横向分量         j t t z et ez j t t et z et t ez H e e j j                           p 纵向分量 p 横向分量 p 如果赫兹电矢量有横向分量，其必然不是TM波 导波场论 7

2.2用位函数法求解波导中的扬 口我们研究的是沿2方向传播的波，所以可以令： I=e.0(p.q)e 口将上式代入方程得： 2i+2i=0→0+(+y)p=0 i=jogeVx1。 H=joseio(V,+e)xedp.q)e i=joseV,×e(p,q)e 导波场论 8

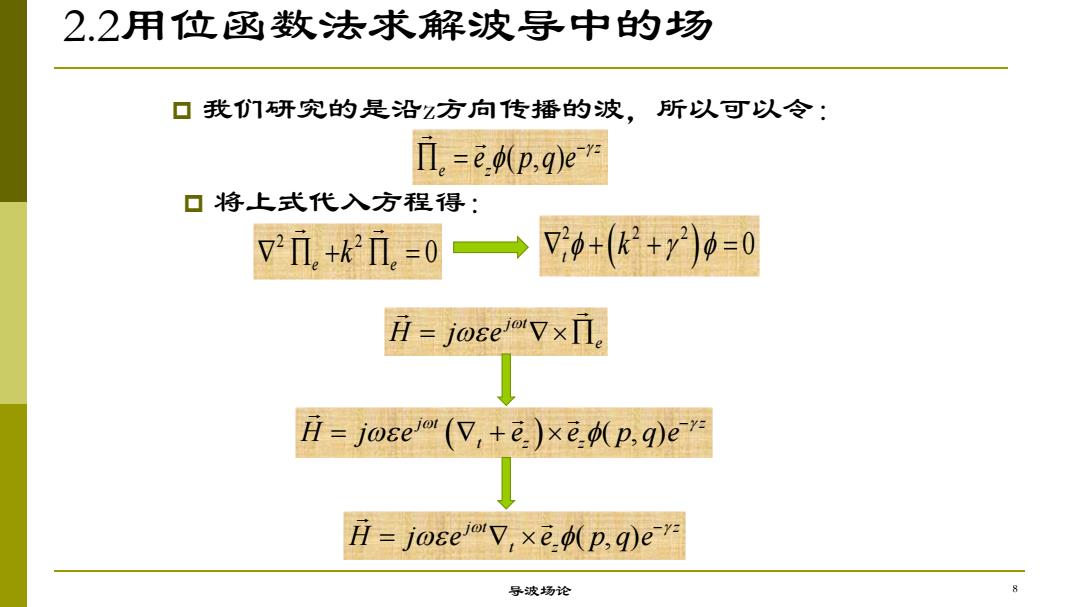
2.2用位函数法求解波导中的场 导波场论 p 我们研究的是沿z方向传播的波，所以可以令： ( , ) z e z e p q e        p 将上式代入方程得： 2 2 0 e e   k       2 2 2 0 t    k    j t e H j e       ( , ) j t t z H z j e e p q e             ( , ) z z t z j H t j e e e p q e             8

2.2用位函数法求解波导中的场 E=K2I.+V(V.TI.)elo E=[k2(p,9)e+[V-(e.p,9g)e)]e -定e-e(又e8* =k2ede r=tio+yepe re-yeV er E.=e(k2+y2）e+o E=-yeTo De y: 导波场论 9

2.2用位函数法求解波导中的场 导波场论   2 2 z j t E z z e k e          j t t z Et e e         导波场论 2 ( ) j t e e E k e               2 2 2 2 ( , ) ( ( , ) ) z z z z z j t z j t j t t j t j t t z z z j t z z z z k e k e E e p q e e p q e e e k e e z e e e e e e e                                                                 9

2.2用位数法求解波导中的扬 0+k+)=0 为横向坐标的标量 E=-ye,e 函数，用这个方程组来 E=(K2+y）ee+ 解TM波的问题是很方 便的。 H,=josey xed(p,q)e 口由于 与 成比例，故在理想导体的边 界上有： =0 导波场论 10

2.2用位函数法求解波导中的场 导波场论 p 为横向坐标的标量 函数，用这个方程组来 解TM波的问题是很方 便的。  p 由于  与 E z 成比例，故在理想导体的边 界上有：   0     2 2 2 2 2 0 ( , ) t z t z j t z z z j t t j t t t z k E e E e k e H j e q e e p e                                  10