
Prior probability(先验概率) Prior or unconditional probabilities(无条件概率)of propositions 在没有任何其它信息存在的情况下关于命题的信度 e.g.,P(Cavity true)=0.1 and P(Weather sunny)=0.72 correspond to belief prior to arrival of any (new)evidence Probability distribution gives values for all possible assignments: 概率分布给出一个随机变量所有可能取值的概率 e.g.,P(Weather)=<0.72,0.1,0.08,0.1>(normalized ( 化的),i.e.,sums to1) 口卡B·三4色进分双0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Prior probability(先验概率) Prior or unconditional probabilities(无条件概率) of propositions 在没有任何其它信息存在的情况下关于命题的信度 e.g., P(Cavity = true) = 0.1 and P(Weather = sunny) = 0.72 correspond to belief prior to arrival of any (new) evidence Probability distribution gives values for all possible assignments: 概率分布给出一个随机变量所有可能取值的概率 e.g., P(Weather) = <0.72, 0.1, 0.08, 0.1> (normalized(归一 化的), i.e., sums to 1)

Prior probability(先验概率) Joint probability distribution for a set of random variables gives the probability of every atomic event on those random variables (i.e., every sample point) 联合概率分布给出一个随机变量集的值的全部组合的概率 e.g.,P(Weather,Cavity)=a 4 x 2 matrix of values: Weather sunny rainy doudy snow Cavity true 0.1440.02 0.016 0.02 Cavity =false 0.576 0.08 0.064 0.08 Every question about a domain can be answered by the joint distribution because every event is a sum of sample points 4口◆4⊙t4三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Prior probability(先验概率) Joint probability distribution for a set of random variables gives the probability of every atomic event on those random variables (i.e., every sample point) 联合概率分布给出一个随机变量集的值的全部组合的概率 e.g., P(Weather, Cavity) = a 4 × 2 matrix of values: Weather = sunny rainy doudy snow Cavity = true 0.144 0.02 0.016 0,02 Cavity = false 0.576 0.08 0.064 0.08 Every question about a domain can be answered by the joint distribution because every event is a sum of sample points

Probability for continuous variables Express distribution as a parameterized(参数化的)function of value: P(X=x)=U18,26(x)=uniform(均匀分布)density between 18 and 26 0.125 18 dx 26 Here P is a density;integrates to 1. P(X=20.5)=0.125 means IimP(20.5≤X≤20.5+dx)/dx=0.125 dx-→0 口卡回t·三4色,是分Q0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Probability for continuous variables Express distribution as a parameterized(参数化的)function of value: P(X = x) = U[18, 26](x) = uniform(均匀分布)density between 18 and 26 Here P is a density; integrates to 1. P(X = 20.5) = 0.125 means lim dx→0 P(20.5 ≤ X ≤ 20.5 + dx)/dx = 0.125
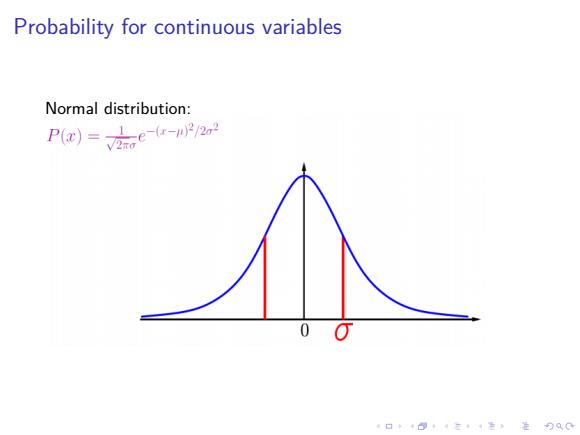
Probability for continuous variables Normal distribution: P(a)=ge-(-22 4口◆4⊙t1三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Probability for continuous variables Normal distribution:

Conditional probability(条件概率) Conditional or posterior probabilities(后验概率)P(alb) e.g.,P(cavity toothache)=0.8 i.e.,given that toothache is all I know Notation for conditional distributions(条件概率分布): P(Cavity Toothache)=a 2 x 2 matrix of values If we know more,e.g.,cavity is also given,then we have P(cavity toothache,cavity)=1 New evidence may be irrelevant,allowing simplification,e.g., P(cavity toothache,sunny)=P(cavity toothache)=0.8 This kind of inference,sanctioned by domain knowledge,is crucial 口卡B·三4色进分双0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Conditional probability(条件概率) Conditional or posterior probabilities(后验概率)P(a|b) e.g., P(cavity|toothache) = 0.8 i.e., given that toothache is all I know Notation for conditional distributions(条件概率分布): P(Cavity|Toothache) = a 2 × 2 matrix of values If we know more, e.g., cavity is also given, then we have P(cavity|toothache, cavity) = 1 New evidence may be irrelevant, allowing simplification, e.g., P(cavity|toothache,sunny) = P(cavity|toothache) = 0.8 This kind of inference, sanctioned by domain knowledge, is crucial