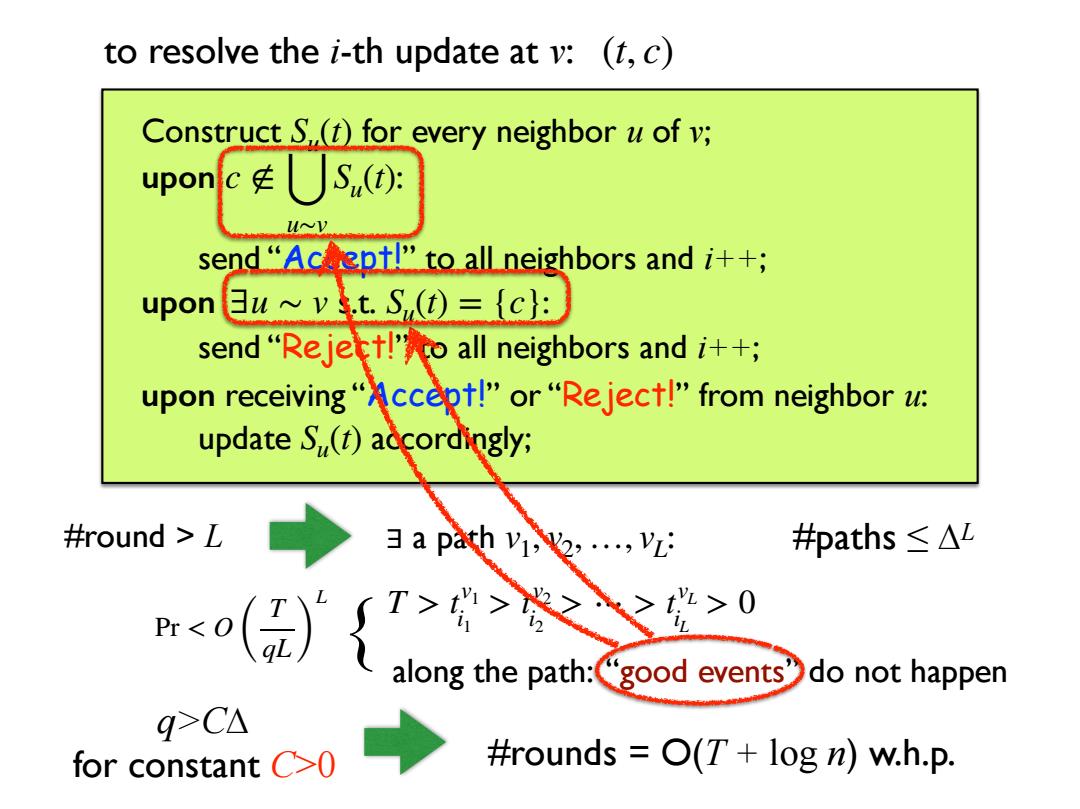
to resolve the i-th update at v:(t,c) Construct S,(t)for every neighbor u of v; upon: send "Aceept!"to all neighbors andi++; upon 3 u~vtS()={c send "Rejet!o all neighbors andi++; upon receiving"Accept!"or "Reject!"from neighbor u: update S(t)adcordingly; #round a path v,...,v: #paths≤△L {g do not happen q>CΔ for constant C>0 #rounds O(T+log n)w.h.p
Construct for every neighbor u of v; upon : send “Accept!” to all neighbors and i++; upon : send “Reject!” to all neighbors and i++; upon receiving “Accept!” or “Reject!” from neighbor u: update accordingly; Su(t) c ∉ ⋃ u∼v Su(t) ∃u ∼ v s.t. Su(t) = {c} Su(t) to resolve the i-th update at v: (t, c) #round > L ∃ a path v : 1, v2, …, vL T > t v1 i1 > t v2 i2 > ⋯ > t vL iL > 0 along the path: “good events” do not happen { #paths ≤ ∆L q>C∆ for constant C>0 #rounds = O(T + log n) w.h.p. Pr < O ( T qL ) L
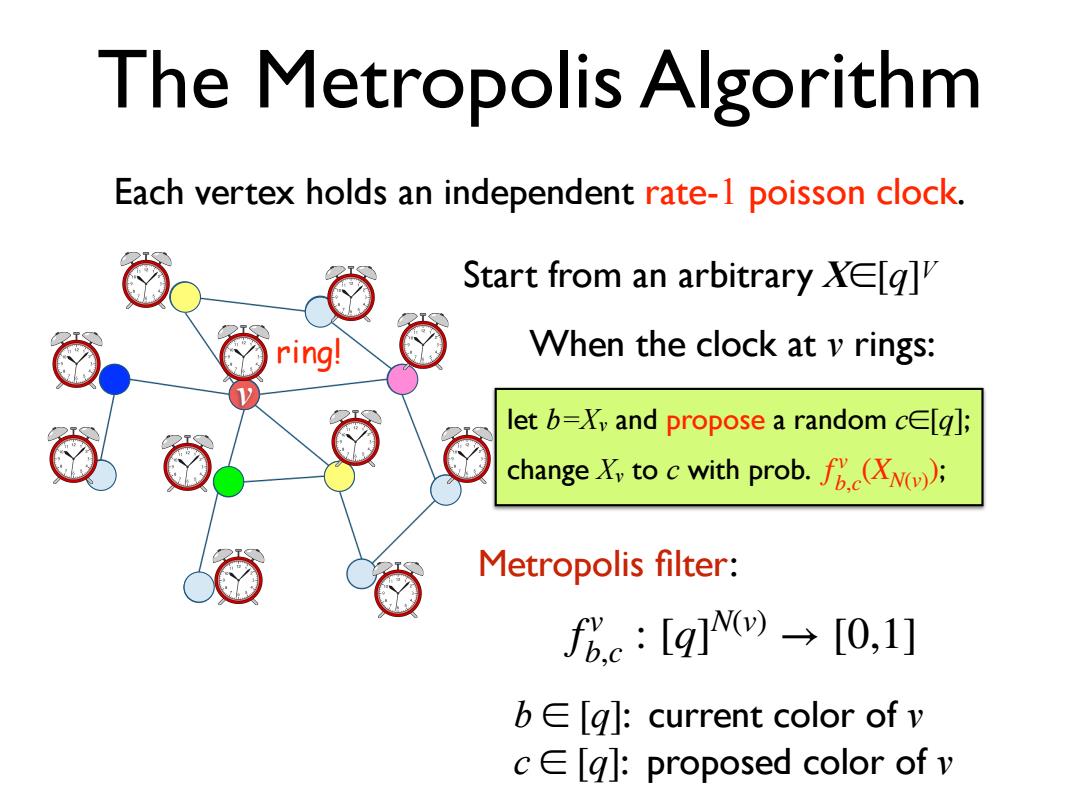
The Metropolis Algorithm Each vertex holds an independent rate-1 poisson clock. Start from an arbitrary XE[g] ring! When the clock at v rings: letb=X,and propose a random ce∈[q小; change X to c with prob.)); Metropolis filter: f6c:[q]→[0,1] b∈[q小:current color of v ce g]:proposed color of v
The Metropolis Algorithm let b=Xv and propose a random c∈[q]; change Xv to c with prob. f ; v b,c (XN(v) ) Start from an arbitrary X∈[q]V Metropolis filter: f v b,c : [q] N(v) → [0,1] b ∈ [q]: current color of v c ∈ [q]: proposed color of v Each vertex holds an independent rate-1 poisson clock. When the clock at v rings: v ring!