
图的术语(续) ●有向图G=(V,E,p),p(e)=(w,) ●u是e的起点,v是e的终点 。假设u≠v,u邻接到v,v从u邻接 ·有向图中顶点的出度和入度 。dc+(y)=以v为始点的边的条数,deg(v) 。dg(y)=以v为终点的边的条数,deg() ·有向图中各顶点的出度之和等于入度之和。 Evey deg"(v)=Evev deg (v)=El ·有向图的底图
图的术语(续) 有向图G =(V, E, ϕ), ϕ(e)=(u, v) u是e的起点,v是e的终点 假设 u≠v,u邻接到v,v从u邻接 有向图中顶点的出度和入度 dG +(v) = 以v为始点的边的条数, deg+(v) dG - (v) = 以v为终点的边的条数, deg- (v) 有向图中各顶点的出度之和等于入度之和。 Σv∈V deg+(v) = Σv∈V deg- (v) =|E| 有向图的底图
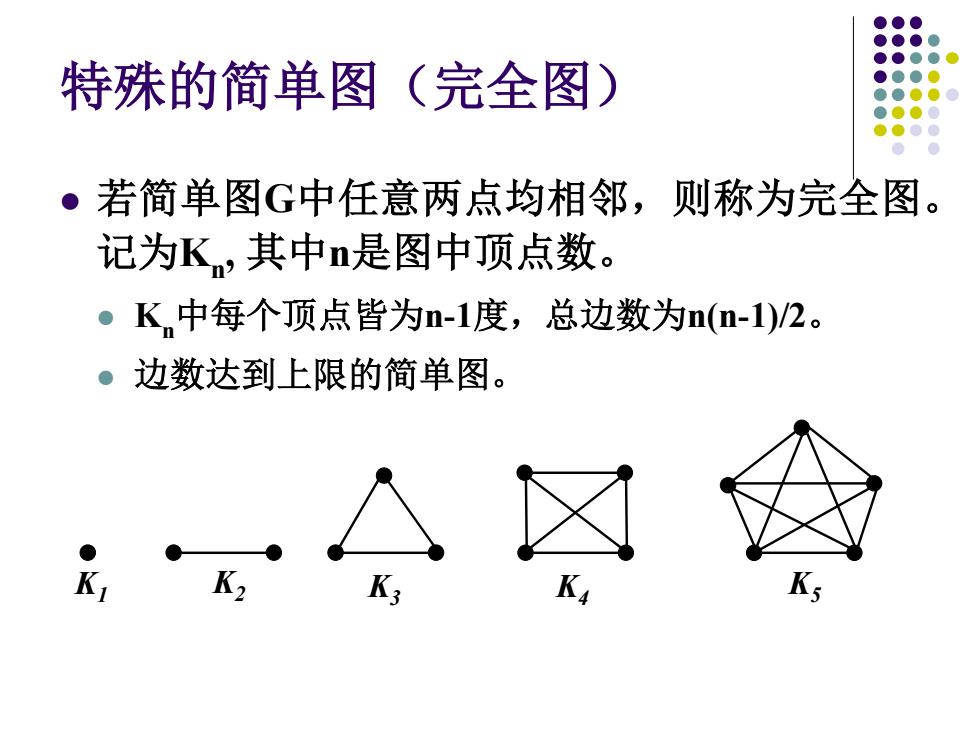
特殊的简单图(完全图) ●若简单图G中任意两点均相邻,则称为完全图。 记为K,其中是图中顶点数。 ●K中每个顶点皆为n-1度,总边数为n(m-1)/2。 。边数达到上限的简单图。 Ks
特殊的简单图(完全图) 若简单图G中任意两点均相邻,则称为完全图。 记为Kn, 其中n是图中顶点数。 Kn中每个顶点皆为n-1度,总边数为n(n-1)/2。 边数达到上限的简单图。 K3 K1 K2 K4 K5
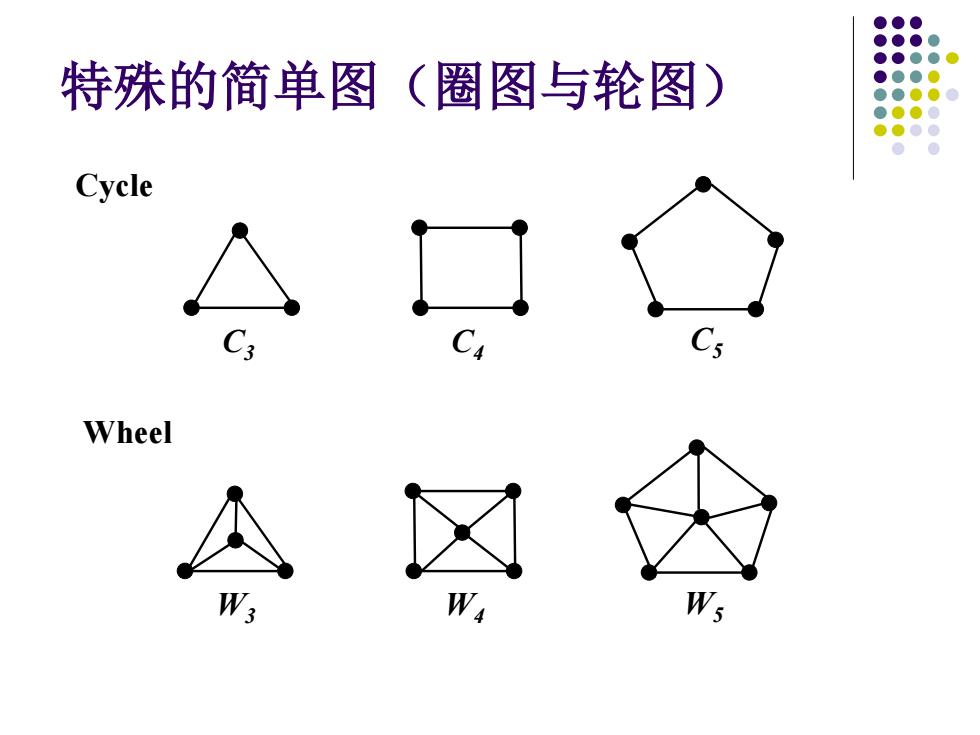
特殊的简单图(圈图与轮图) Cycle 5 Wheel W
特殊的简单图(圈图与轮图) C3 C4 C5 W3 W4 W5 Cycle Wheel
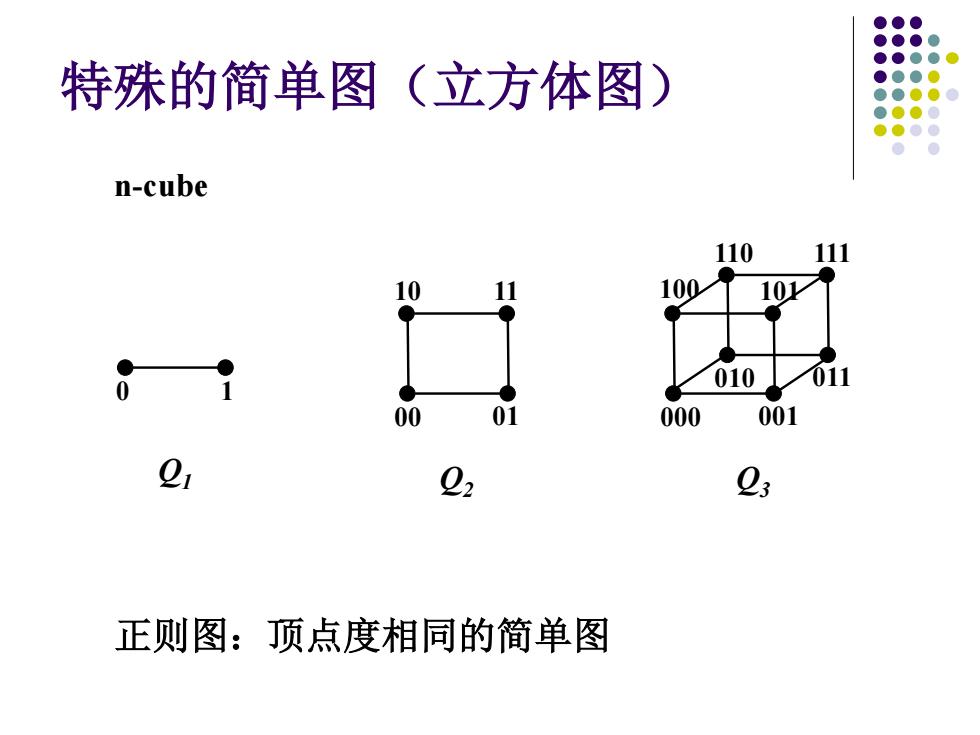
特殊的简单图( 立方体图) n-cube 110 111 0 11 00 101 010 011 00 01 000 001 21 02 23 正则图:顶点度相同的简单图
特殊的简单图(立方体图) Q1 0 1 Q2 10 11 00 01 Q3 100 101 000 001 110 111 010 011 n-cube 正则图:顶点度相同的简单图
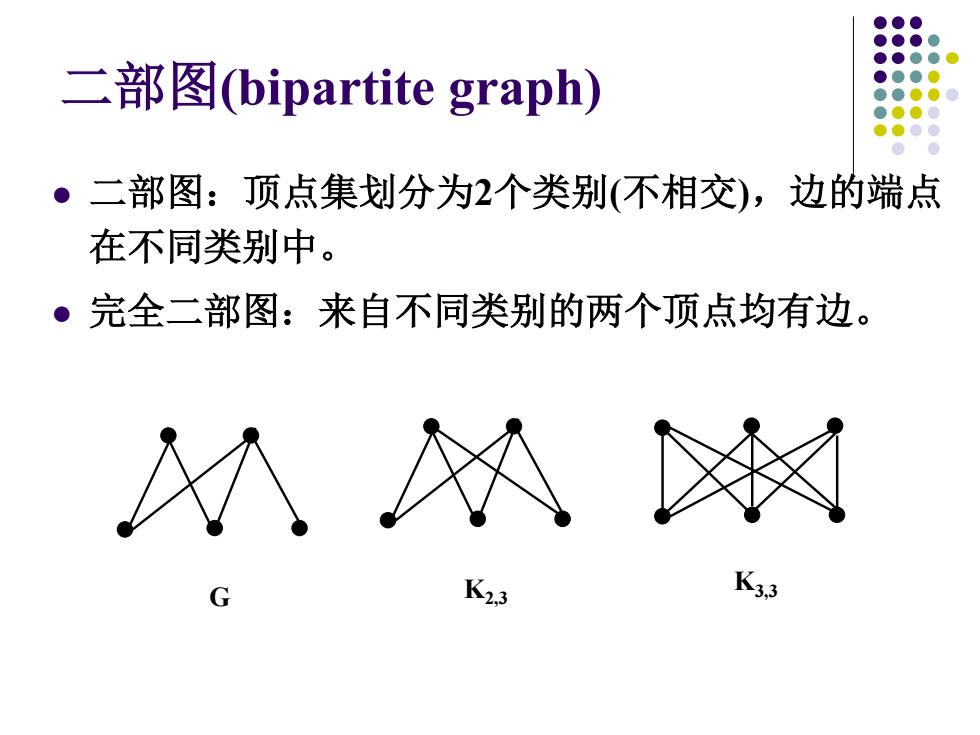
二部图(bipartite graph) ·二部图:顶点集划分为2个类别(不相交),边的端点 在不同类别中。 ·完全二部图:来自不同类别的两个顶点均有边。 K2,3 33
二部图(bipartite graph) 二部图:顶点集划分为2个类别(不相交),边的端点 在不同类别中。 完全二部图:来自不同类别的两个顶点均有边。 K2,3 G K3,3