南京大学：《离散数学》课程教学资源（PPT课件讲稿）图论初步——基本概念

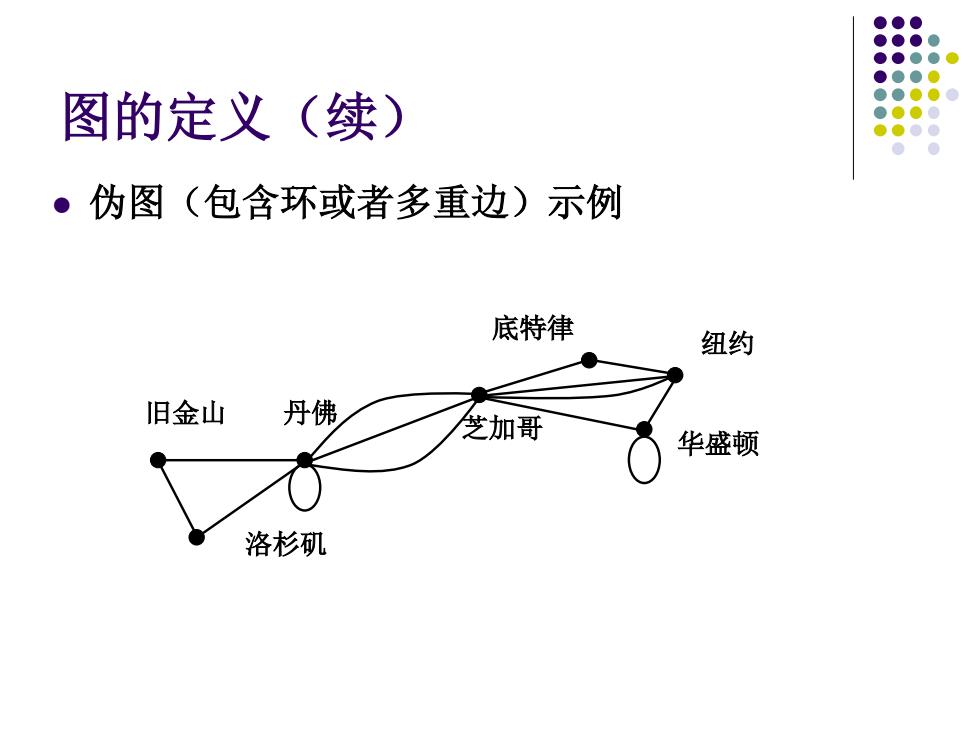
图的定义（续) ·伪图（包含环或者多重边）示例 底特律 纽约 旧金山 丹佛 芝加哥 华盛顿 洛杉矶

图的定义（续）  伪图（包含环或者多重边）示例 洛杉矶 旧金山 丹佛 芝加哥 华盛顿 纽约 底特律

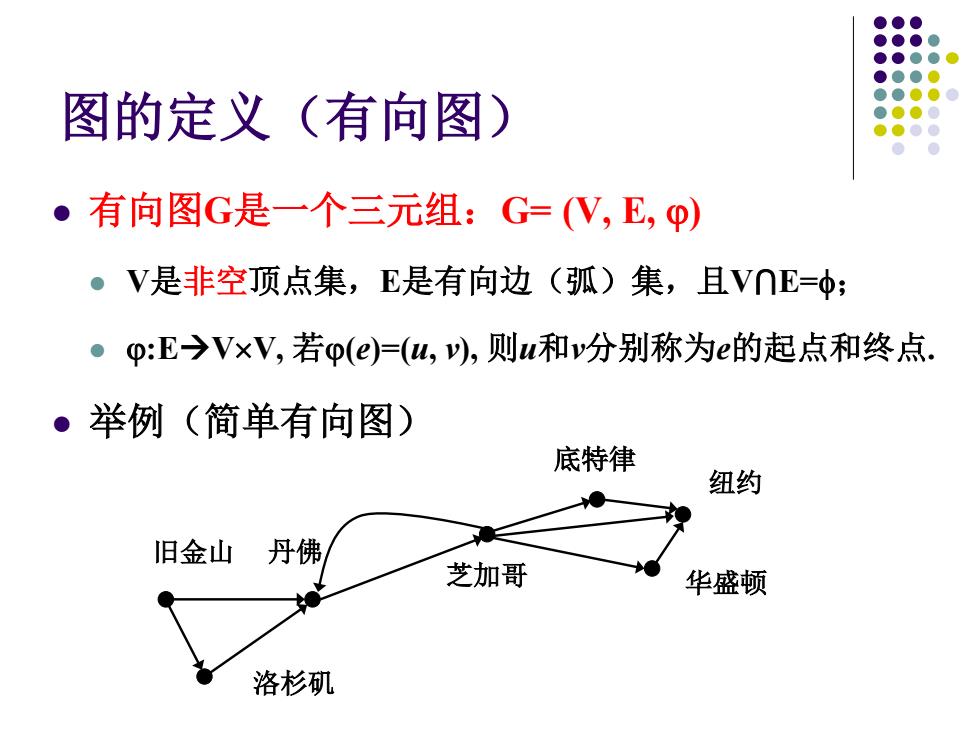
图的定义（有向图） ·有向图G是一个三元组：G=(V,E,φ) 。V是非空顶点集，E是有向边（弧）集，且V∩E=中； ●p:E→VxV,若p(e)=(w,v吵，则u和分别称为e的起点和终点. ·举例（简单有向图) 底特律 纽约 旧金山丹佛 芝加哥 华盛顿 洛杉矶

图的定义（有向图）  有向图G是一个三元组：G= (V, E, ϕ)  V是非空顶点集，E是有向边（弧）集，且V⋂E=φ；  ϕ:EV×V, 若ϕ(e)=(u, v), 则u和v分别称为e的起点和终点.  举例（简单有向图） 洛杉矶 旧金山 丹佛 芝加哥 华盛顿 纽约 底特律

图模型 ·交通网络 。航空、公路、铁路 ·信息网络 。万维网图(Web Graph) 。引用图(Citation Graph) ·社会网络 。熟人关系图 ·合作图，好莱坞图 。呼叫图 ·体育（循环赛的图模型)

图模型  交通网络  航空、公路、铁路  信息网络  万维网图（Web Graph）  引用图（Citation Graph）  社会网络  熟人关系图  合作图，好莱坞图  呼叫图  体育（循环赛的图模型）

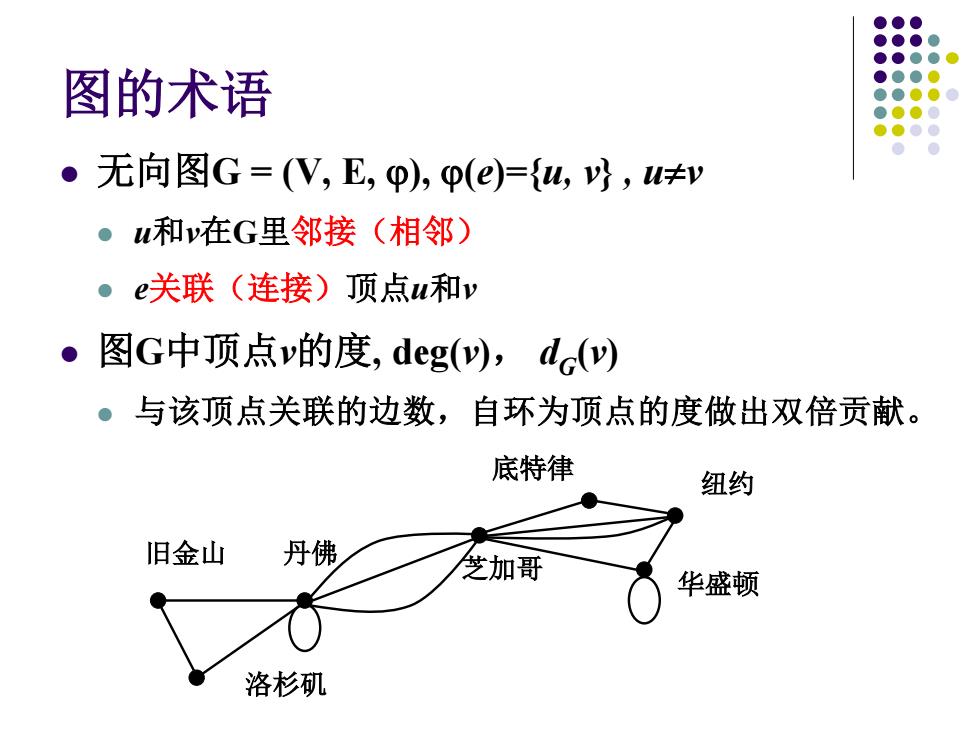
图的术语 ·无向图G=(V,E,p),p()={w,,u≠y 。u和v在G里邻接（相邻） ●e关联（连接）顶点u和v 。图G中顶点v的度，deg(y),dc() ●与该顶点关联的边数，自环为顶点的度做出双倍贡献。 底特律 纽约 旧金山 丹佛 芝加哥 华盛顿 洛杉矶

图的术语  无向图G = (V, E, ϕ), ϕ(e)={u, v} , u≠v  u和v在G里邻接（相邻）  e关联（连接）顶点u和v  图G中顶点v的度, deg(v)， dG(v)  与该顶点关联的边数，自环为顶点的度做出双倍贡献。 洛杉矶 旧金山 丹佛 芝加哥 华盛顿 纽约 底特律

握手定理 ●无向图G有m条边，n个顶点y,ym ∑dy,)=2m i=1 ·推论：无向图中奇数度顶点必是偶数个

握手定理  无向图G有m条边，n个顶点v1, …vn.  推论：无向图中奇数度顶点必是偶数个。 d v m n i i ( ) 2 1 ∑ = =