上游充通大¥ SHANGHAI JIAO TONG UNIVERSITY 噪声 阈值β 信号 正 “不 之“是” 决策的标准Xc的位置决 拒斥 击中 定了操作者的行为是保 守还是冒进 Xc 漏报 误报 对于一个给定的XC的值,该值是由上图中两条曲线高度值的比 例决定的。 Xc若向右面,B值大于1, 这就会造成“是”反应减少,击中 也较少,而误报也较少。 Xc若向左面,B值小于1,这就会造成“是”反应增多,击中 也较多,而误报也较多 以上两种情况中是B值和Xc决定了反应偏向或反应标准
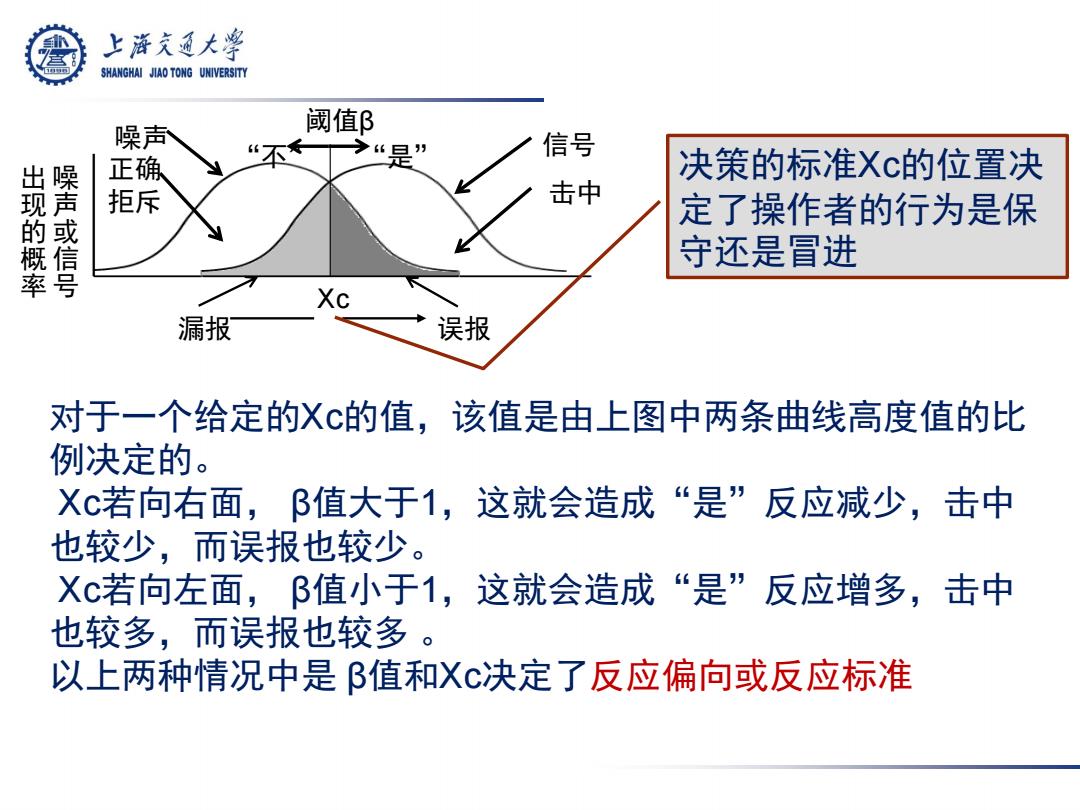
噪 声 或 信 号 出 现 的 概 率 阈值β “不” “是” 信号 击中 噪声 正确 拒斥 Xc 漏报 误报 决策的标准Xc的位置决 定了操作者的行为是保 守还是冒进 对于一个给定的Xc的值,该值是由上图中两条曲线高度值的比 例决定的。 Xc若向右面, β值大于1,这就会造成“是”反应减少,击中 也较少,而误报也较少。 Xc若向左面, β值小于1,这就会造成“是”反应增多,击中 也较多,而误报也较多 。 以上两种情况中是 β值和Xc决定了反应偏向或反应标准
上游充通大¥ SHANGHAI JIAO TONG UNIVERSITY 刺激 阈值β 信号 噪声 噪声、 “不→“是” 信号 击中 误报 正确 有 拒斥 击中 反 (H) (FA) 漏报 正确拒斥 无 (M) (CR) Xc 漏报 X→误报 每格中的实际概率值都可通 绘制标准左右两边不同情 过获得的数据计算得到 形的概率分布曲线 如果两种曲线下分布的面积大小和形状相同,B值就为1那 么在这种情形中P(H)=P(CR)和P(M)=P(FA),这是典型的“中 性标准”设置
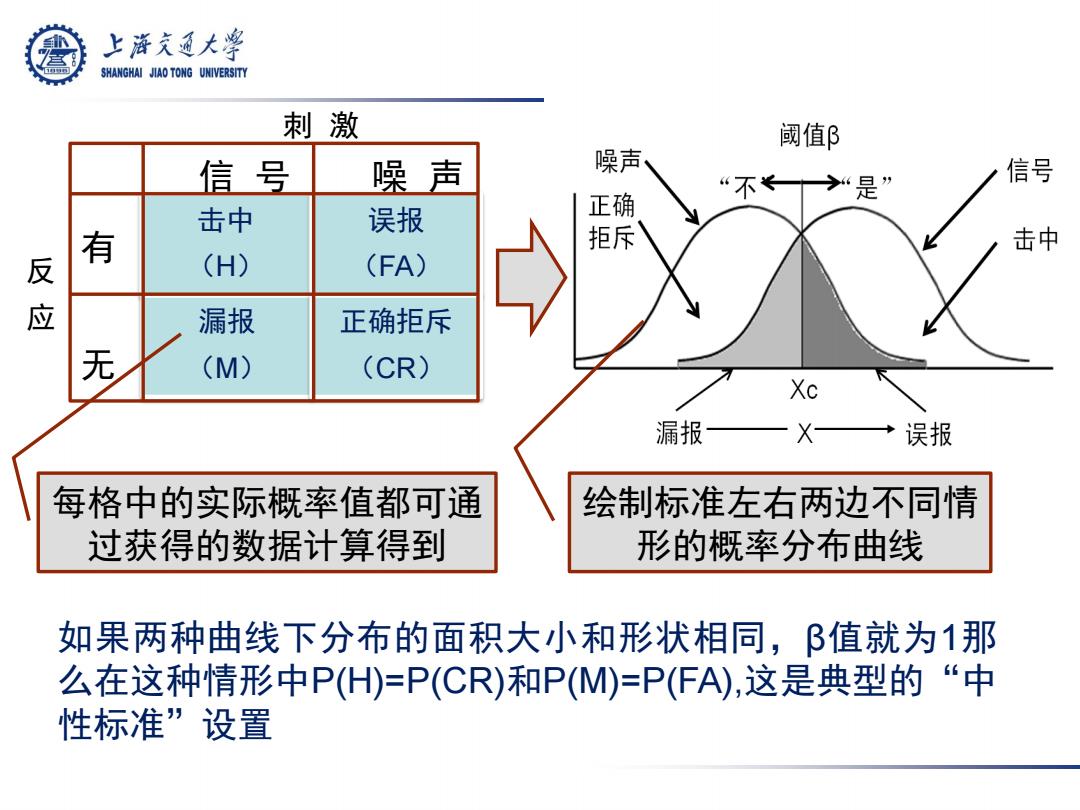
击中 (H) 误报 (FA) 漏报 (M) 正确拒斥 (CR) 信 号 刺 激 噪 声 反 应 有 无 每格中的实际概率值都可通 过获得的数据计算得到 绘制标准左右两边不同情 形的概率分布曲线 如果两种曲线下分布的面积大小和形状相同,β值就为1那 么在这种情形中P(H)=P(CR)和P(M)=P(FA),这是典型的“中 性标准”设置

上游充通大学 SHANGHAI JIAO TONG UNIVERSITY 信号检测论能够根据以下两种情况来准确设置最佳 的B值的位置: (1)检测信号的可能性; (2)四种可能结果的付出和利益。 下面介绍: 信号概率的影响; ©最佳β值设置中的奖惩问题; ©确定B值中人的操作问题
信号检测论能够根据以下两种情况来准确设置最佳 的β值的位置: (1)检测信号的可能性; (2)四种可能结果的付出和利益。 下面介绍: 信号概率的影响; 最佳β值设置中的奖惩问题; 确定β值中人的操作问题

上游充通大¥ SHANGHAI JIAO TONG UNIVERSITY ©信号概率 信号比平时发生的要多,误报和漏报造成的损失 相等,击中和正确抗拒的收益也相等时,最佳操 作就是较少漏报和误报的错误。当Xc的位置处在 两条曲线的交接面上,即B=1时,操作最佳。 如果信号经常发生,标准就会降低;相反,若信 号发生的概率较少,那么β值向反方向调整。 通常在信号和噪声概率变化是,最佳B的调整如 下式所示: Bopr P(N)/P(S) 式(2.2)
信号概率 信号比平时发生的要多,误报和漏报造成的损失 相等,击中和正确抗拒的收益也相等时,最佳操 作就是较少漏报和误报的错误。当Xc的位置处在 两条曲线的交接面上,即β=1时,操作最佳。 如果信号经常发生,标准就会降低;相反,若信 号发生的概率较少,那么β值向反方向调整。 通常在信号和噪声概率变化是,最佳β的调整如 下式所示: ( ) / ( ) opt P N P S 式(2.2)

上游充通大学 SHANGHAI JIAO TONG UNIVERSITY 的值会随P(S)值得增加而减少(产生冒险者) opt 阈值B 处于最佳β值 噪声 信号 时,操作并不 正确 “不一今“是” 是完美的,两 拒斥 击中 曲线重叠处的 产最 而生佳 漏报、误报 值 依然寻在 Xc 漏报 X 误报 在给定的信号强度和敏感性水平时,最佳β值时的操作是能预期 的最有操作 与计算β值公式的区别:最佳β值讲的是β值的理想值,它的设置 是由在特定环境中的噪声和信号的概率比例决定的。相反,事 实上的β值是由操作者决定的,其数值来源于经验数据
opt 的值会随P(S)值得增加而减少(产生冒险者) 左移, 从而 产生 最佳 β值 处于最佳β值 时,操作并不 是完美的,两 曲线重叠处的 漏报、误报 依然寻在 在给定的信号强度和敏感性水平时,最佳β值时的操作是能预期 的最有操作 与计算β值公式的区别:最佳β值讲的是β值的理想值,它的设置 是由在特定环境中的噪声和信号的概率比例决定的。相反,事 实上的β值是由操作者决定的,其数值来源于经验数据