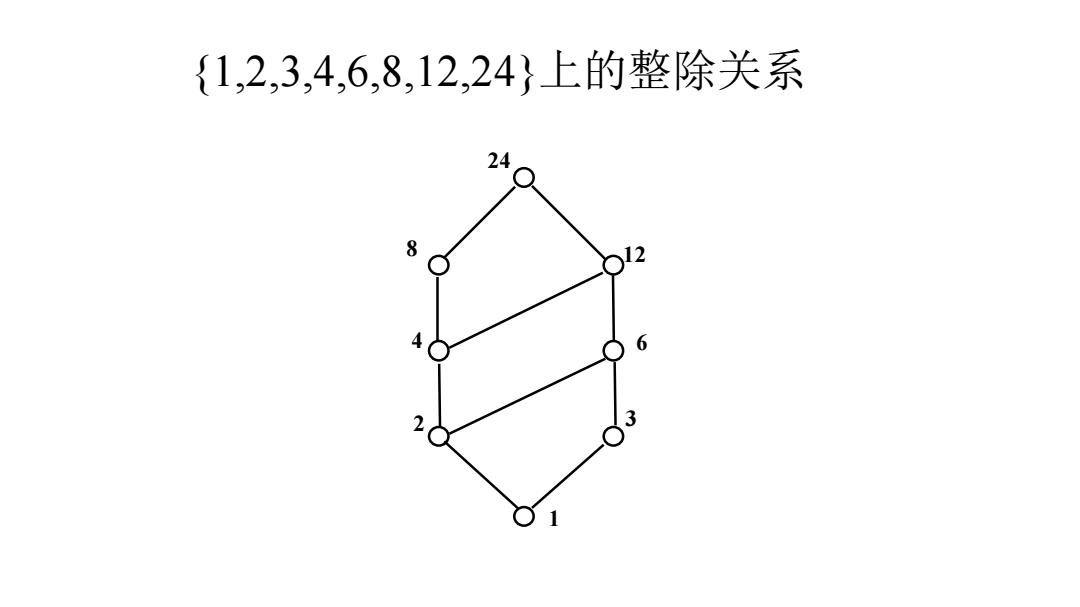
{1,2,3,4,6,8,12,24}上的整除关系 24 8 12 6 3
24 8 4 6 2 3 12 1 {1,2,3,4,6,8,12,24}上的整除关系

偏序集中的特殊元素:极大(小) ·x是偏序集<A,≤>中的极大元iff ·对任意y∈A,若x≤y,则x=y ·x是偏序集<A,≤>中的极小元if ·对任意y∈A,若y≤x,则x=y ·有关极大元与极小元的讨论 ·有穷偏序集一定有极大(小)元 没有比它更小(大的了1 ·不一定唯一 ·一个元素可能兼为极大(小)元?
偏序集中的特殊元素 :极大(小) • x是偏序集<A,≼>中的极大元iff. • 对任意y∈A,若x≼y, 则x=y • x是偏序集<A,≼>中的极小元iff. • 对任意y∈A,若y≼x, 则x=y • 有关极大元与极小元的讨论 • 有穷偏序集一定有极大(小)元 • 不一定唯一 • 一个元素可能兼为极大(小)元? 没有比它更小(大)的了!
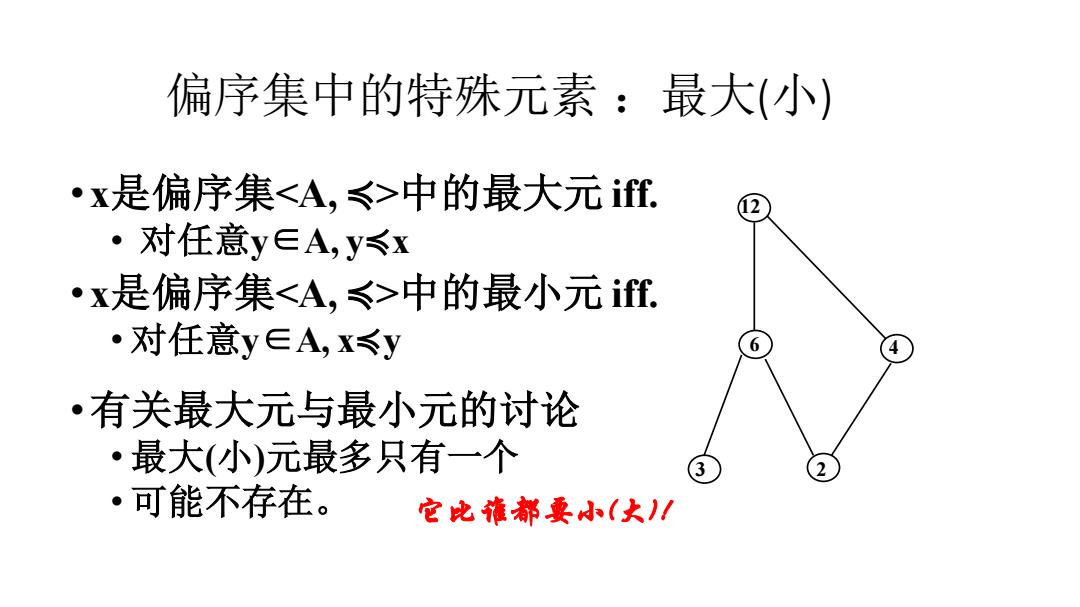
偏序集中的特殊元素:最大(小) ·x是偏序集<A,≤>中的最大元f 2 ·对任意y∈A,y≤x ·x是偏序集<A,≤>中的最小元f. ·对任意y∈A,x≤y 6 ·有关最大元与最小元的讨论 •最大(小)元最多只有一个 3 2 ·可能不存在。 它比准都要小(大)1
偏序集中的特殊元素 :最大(小) • x是偏序集<A, ≼>中的最大元 iff. • 对任意y∈A, y≼x • x是偏序集<A, ≼>中的最小元 iff. • 对任意y∈A, x≼y •有关最大元与最小元的讨论 • 最大(小)元最多只有一个 • 可能不存在。 它比谁都要小(大)! 12 3 6 2 4

问题4:如何证明这个定理? Suppose S is a finite partially ordered set.Afunction f:S-N satisfying that if a b then f(a)<f(b)is called a consistent enumeration of S. Theorem 14.1:There exists a consistent enumeration for any finite poset A What to prove: Suppose S is a finite poset with n elements.Then there exists a consistent enumeration f:S-{1,2,...,n}. By induction on the number n of elements in S. n=1,S={s):f(s)=1 is a consistent enumeration of S. H:assume the theorem holds for posets with fewer than n elements I:Let a E S be a minimal element in S Let T S/{a).Then T is a finite poset with n-1 elements;By H,T admits a consistent enumeration; sayg:T→{1,2,,n-1. ·Define f:S→{1,2,,n )+1 if x=a ifx≠a
问题4:如何证明这个定理? Suppose S is a finite partially ordered set. A function 𝑓: 𝑆 → 𝑁 satisfying that if 𝑎 ≺ 𝑏 then 𝑓(𝑎) < 𝑓(𝑏) is called a consistent enumeration of S. What to prove: Suppose S is a finite poset with n elements. Then there exists a consistent enumeration 𝑓: 𝑆 → {1, 2, . . . , 𝑛}. By induction on the number n of elements in S. • n=1, S = {s}: f (s) = 1 is a consistent enumeration of S. • H: assume the theorem holds for posets with fewer than n elements • I: Let 𝑎 ∈ 𝑆 be a minimal element in S • Let 𝑇 = 𝑆/{𝑎}. Then T is a finite poset with n − 1 elements; By H, T admits a consistent enumeration; say 𝑔: 𝑇 → {1, 2, . . . , 𝑛 − 1}. • Define 𝑓: 𝑆 → {1, 2, . . . , 𝑛}
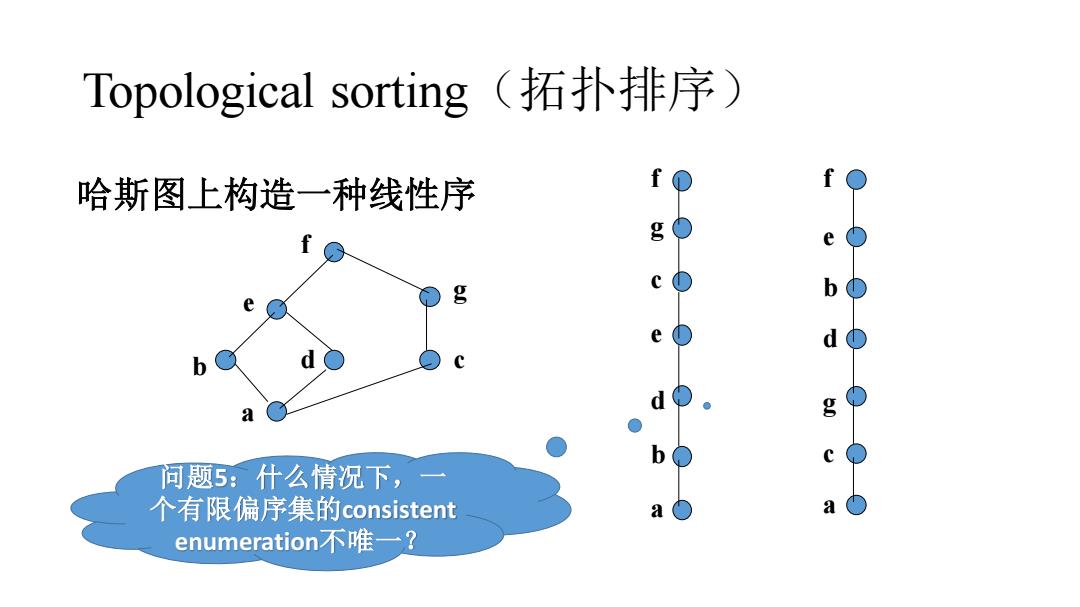
Topological sorting(拓扑排序) 哈斯图上构造一种线性序 g 0 问题5:什么情况下,一 个有限偏序集的consistent enumeration不唯一?
Topological sorting(拓扑排序) a b d c g e f a b d e c g f a c g d b e f 哈斯图上构造一种线性序 问题5:什么情况下,一 个有限偏序集的consistent enumeration不唯一?