
全序:一种特殊的偏序关系 ·如果对,b∈A,a≤b和b≤a中有一个成立,则a,b可比。 ·设R是A上的偏序关系,如果A中的任意两个元素都是可 比的,则称R是A上的全序关系(或线序关系) ·举例(全序) 。实数集上的“不大于”关系≤、基于拉丁字母表的字典顺序
全序:一种特殊的偏序关系 • 如果对a, bA,a≼b和b≼a中有一个成立,则a,b可比。 • 设R是A上的偏序关系,如果A中的任意两个元素都是可 比的,则称R是A上的全序关系(或线序关系) • 举例(全序) • 实数集上的“不大于” 关系、基于拉丁字母表的字典顺序

偏序集上的“小于”关系及覆盖 ·设<A,≤>是偏序集 ·A上的“小于”关系<定义如下: x<y iff x≤yAx≠y ·元素y覆盖x定义如下: ·x<y,且不存在zEA使得x<z<y ·表示为:x《y ·“y是x的覆盖” “y是x的直接后继(immediate successor)
偏序集上的“小于”关系及覆盖 • 设<A, ≼> 是偏序集 • A上的“小于”关系≺定义如下: 𝒙 ≺ 𝒚 iff 𝒙 ≼ 𝒚 ∧ 𝒙𝒚 • 元素y覆盖x定义如下: • x≺y,且不存在zA使得x≺z≺y • 表示为:𝒙 ≪ 𝒚 • “y是x的覆盖” • “y是x的直接后继(immediate successor)
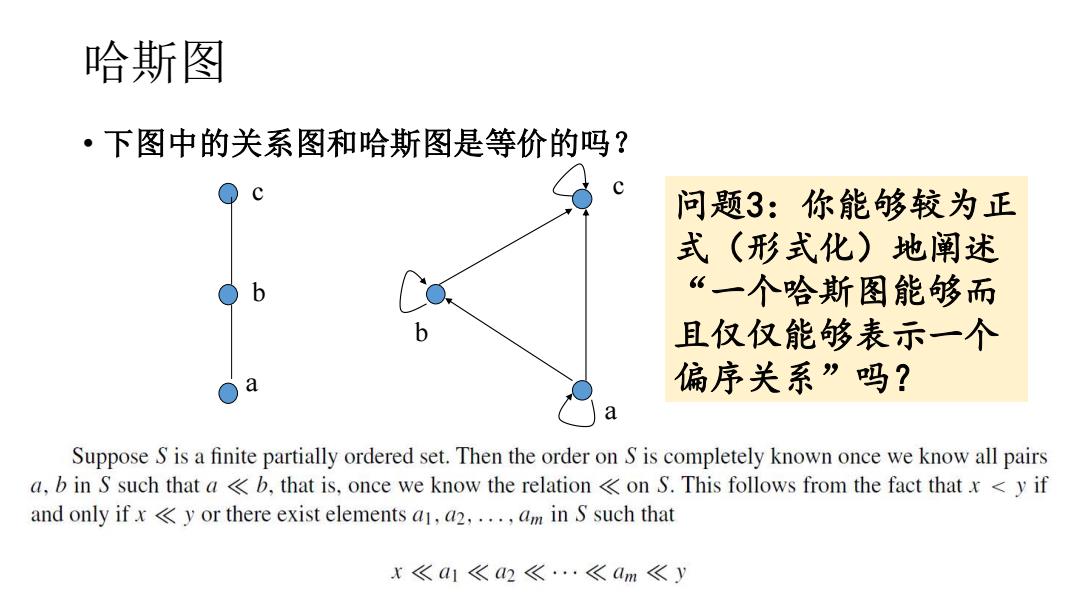
哈斯图 ·下图中的关系图和哈斯图是等价的吗? 问题3:你能够较为正 式(形式化)地阐述 “一个哈斯图能够而 且仅仅能够表示一个 a 偏序关系”吗? Suppose S is a finite partially ordered set.Then the order on S is completely known once we know all pairs a,b in S such that a <b,that is,once we know the relation on S.This follows from the fact thatx <y if and only ifx<y or there exist elements a1,a2,...,am in S such that x《a1《a2《·《am《y
哈斯图 • 下图中的关系图和哈斯图是等价的吗? a b c a b c 问题3:你能够较为正 式(形式化)地阐述 “一个哈斯图能够而 且仅仅能够表示一个 偏序关系”吗?
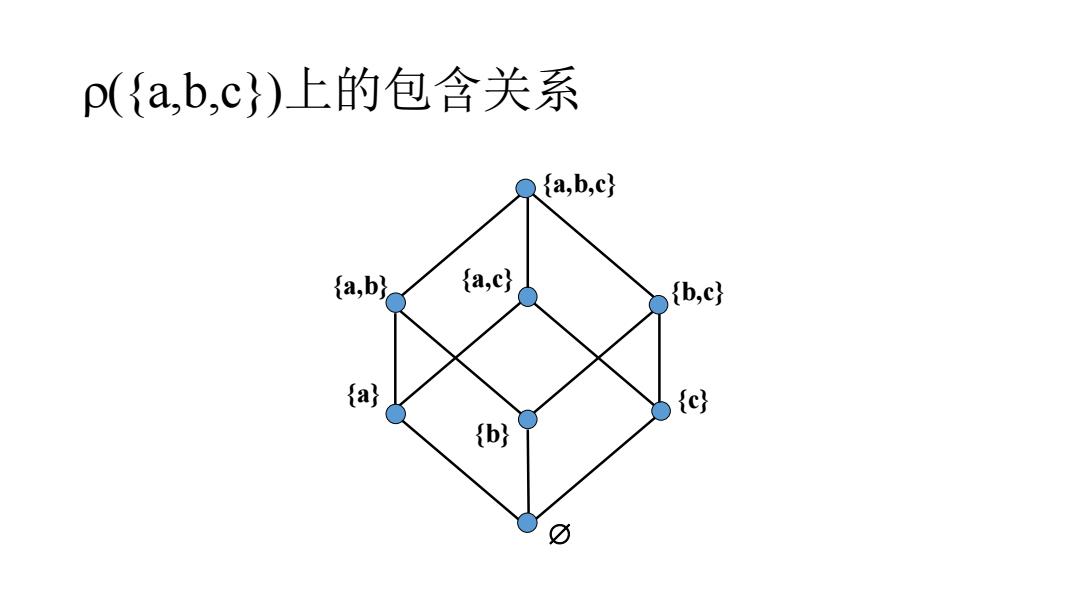
p({a,b,c)上的包含关系 fa,b,c} (a,b) {a,c} b,c} (a) c {b} 0
{a,b,c} {c} {b} {a} {b,c} {a,c} {a,b} ({a,b,c})上的包含关系
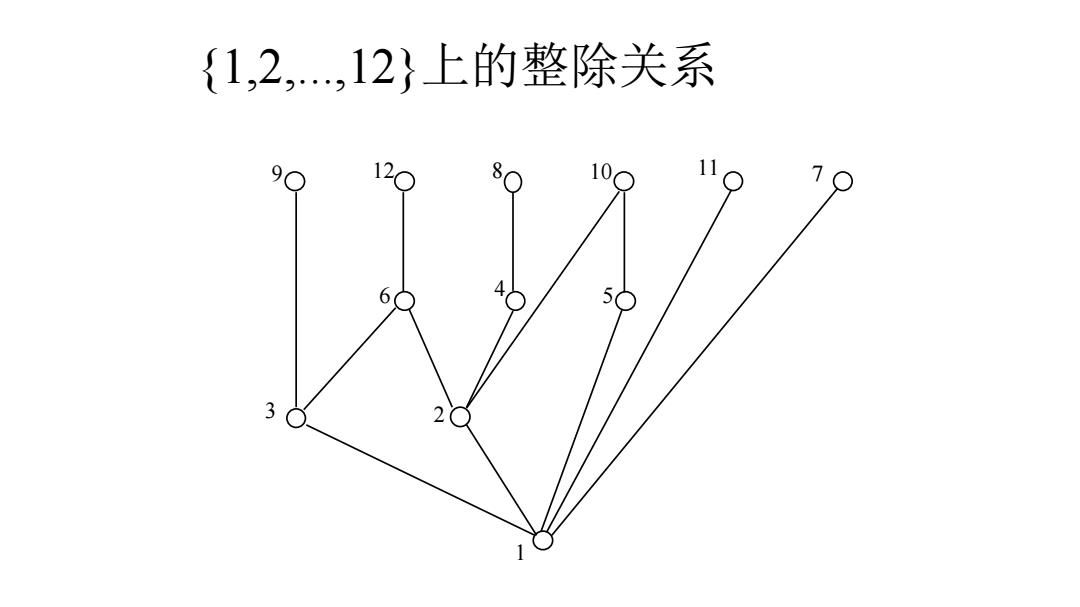
{1,2,12}上的整除关系 9 12O 80 10O 11 60 a 50 3 1
9 12 8 10 11 6 5 4 3 2 1 7 {1,2,...,12}上的整除关系