
或偏摩尔量的含义是:在 等温、等压条件下,在大 偏摩尔量Z3的定义为: 量的定组成系统中,加入 def az 单位物质的量的B物质所 引起广度性质Z的变化值。 Ong JT,p,n.(c≠B) Z称为物质B的某种容量性质Z的偏摩尔量 代入下式并整理得 在等温、等压、保持B物 质以外的所有组分的物 3质的量不变的有限系统 B=1 中,改变dn所引起广度 =Zdn,+Z2dn2+性质Z的变化值。 ∑Zpdnp B=
B , , (c B) B def ( )T p nc Z Z n 偏摩尔量ZB的定义为: ZB称为物质B的某种容量性质Z的偏摩尔量 代入下式并整理得 k , , ( B) B B=1 B d ( ) d T p n c c Z Z n n = = + + + Z n Z n Z n 1 1 2 2 k k d d d k B B B=1 = Z nd 或偏摩尔量的含义是:在 等温、等压条件下,在大 量的定组成系统中,加入 单位物质的量的B物质所 引起广度性质Z的变化值。 在等温、等压、保持B物 质以外的所有组分的物 质的量不变的有限系统 中,改变dnB所引起广度 性质Z的变化值
常见的偏摩尔量定义式有: def av def aU T,p,ncC≠B) ong )T.p.nccca def OH Se def as ong )T.p.ncceB) One T,p,nC(C+B) A def OA def T,p,nC(C+B) ong )T,p.ncc) Z,代表偏摩尔量 Zm.B 代表纯物的摩尔量
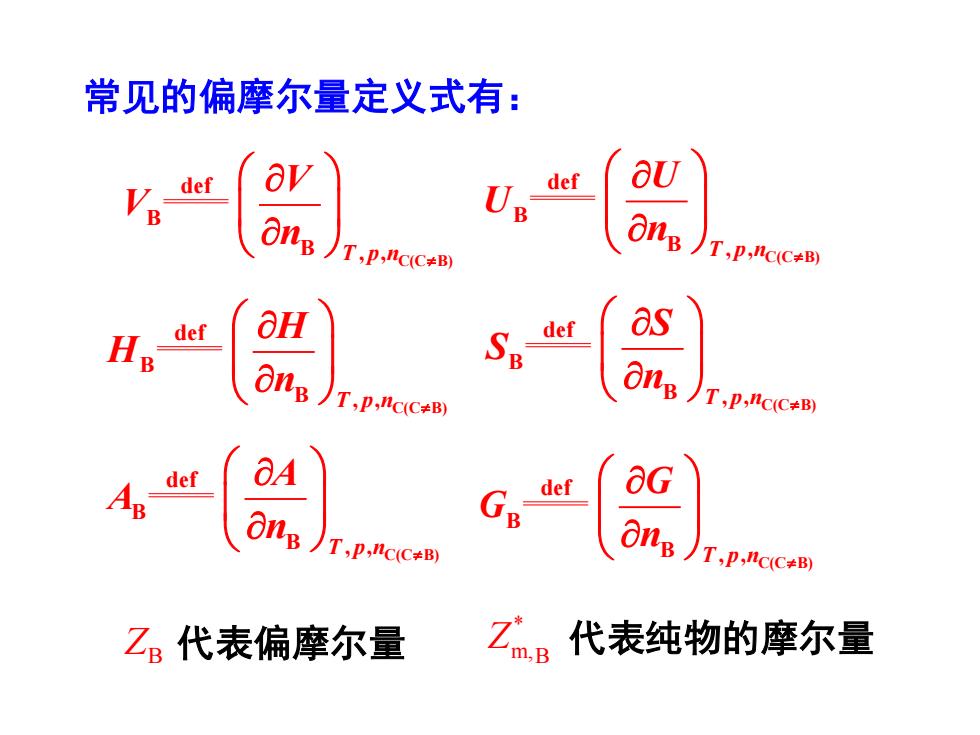
常见的偏摩尔量定义式有: C(C B) B B , , def T p n V V n C(C B) B B , , def T p n U U n C(C B) B B , , def T p n H H n C(C B) B B , , def T p n S S n C(C B) B B , , def T p n A A n C(C B) B B , , def T p n G G n ZB 代表偏摩尔量 代表纯物的摩尔量 * m,B Z

说明 (1)偏摩尔量的含义是:在等温、等压条件下,在大 量的定组成系统中,加入单位物质的量的B物质所 引起广度性质Z的变化值。 或在等温、等压、保持B物质以外的所有组分 的物质的量不变的有限系统中,改变dn所引起广 度性质Z的变化值。 (2)只有广度性质才有偏摩尔量,而偏摩尔量是强 度性质。 (3)纯物质的偏摩尔量就是它的摩尔量。 (4)任何偏摩尔量都是T,p和组成的函数
(1)偏摩尔量的含义是:在等温、等压条件下,在大 量的定组成系统中,加入单位物质的量的B物质所 引起广度性质Z的变化值。 (2) 只有广度性质才有偏摩尔量,而偏摩尔量是强 度性质。 (3) 纯物质的偏摩尔量就是它的摩尔量。 (4) 任何偏摩尔量都是T,p和组成的函数。 或在等温、等压、保持B物质以外的所有组分 的物质的量不变的有限系统中,改变 所引起广 度性质Z的变化值。 B dn 说明

2.偏摩尔量的加和公式 根据偏摩尔量的定义,它与T,和组成有关 在等温等压的条件下,Z的变化由组成的变化引起 k 则dz=Z,dh,+Z,dn,++Zd.=∑Zdn。 在保持偏摩尔量不变的情况下,对上式积分 Z=Z0dm+z小dh,++Z0dn =,乙,+,Z2+.+m乙=∑n乙
2. 偏摩尔量的加和公式 根据偏摩尔量的定义,它与T、p和组成有关 在保持偏摩尔量不变的情况下,对上式积分 1 2 k 1 1 2 2 k k 0 0 0 d d d n n n Z Z n Z n Z n = + + + 则 d d d d Z Z n Z n Z n = + + + 1 1 2 2 k k k B B B=1 = Z nd = + + + n Z n Z n Z 1 1 2 2 k k k B B B=1 = n Z 在等温等压的条件下,Z的变化由组成的变化引起

2.偏摩尔量的加和公式 B=1 这就是偏摩尔量的加和公式,说明系统的总 的容量性质等于各组分偏摩尔量的加和。 例如:系统只有两个组分其物质的量和偏 摩尔体积分别为n,y和 并不是1组分在系统中所占的 体积 V=nK+nv
2. 偏摩尔量的加和公式 这就是偏摩尔量的加和公式,说明系统的总 的容量性质等于各组分偏摩尔量的加和。 k B B B=1 Z=n Z V nV n V = + 1 1 2 2 例如:系统只有两个组分,其物质的量和偏 摩尔体积分别为 n V1 1 , 和 n V2 2 并不是 , ,则系统的总体积为: 1组分在系统中所占的 体积