
Zero and pole The z-transform is most useful when the infinite sum can be expressed in closed form, usually a ratio of polynomials in z(or z). x立z P(2) =-o0 Zero:The value of z for which X()=0 Pole:The value of z for which X()=oo 13
13 Zero and pole ( ) ( ) n ( ) n P z X z x n Q z z =− − = = ◆Zero: The value of z for which X(z) = 0 ◆The z-transform is most useful when the infinite sum can be expressed in closed form, usually a ratio of polynomials in z (or z-1 ). ◆Pole: The value of z for which X(z) =

Example 3.1: Right-sided exponential sequence Determine the z-transform including the ROC in z-plane,and draw a sketch of the pole-zero-plot, given sequence: =awaa≤oT a>1? no DTFT Solution: w之*-2r-2af1Hoe0 1-az z-a Condition of convergence: zero:z=0,pole:z=a RoC:lz 1<lor 14
( ) n n 0 n n n n X z a a z u n z =− − − = = = ( ) 1 0 n n az − = = 1 1 j ae − − 14 Example 3.1: Right-sided exponential sequence zero z pole z a : 0 : = = , xn a un n = ◆Determine the z-transform including the ROC in z-plane,and draw a sketch of the pole-zero-plot, given sequence: Solution: ROC: 1 az o1 rz a − ( ) 1 1 1 1 az az − − − = − a 1 DTFT z z a = − 0 a 1? no DTFT 1 1 1 az = − − Condition of convergence:
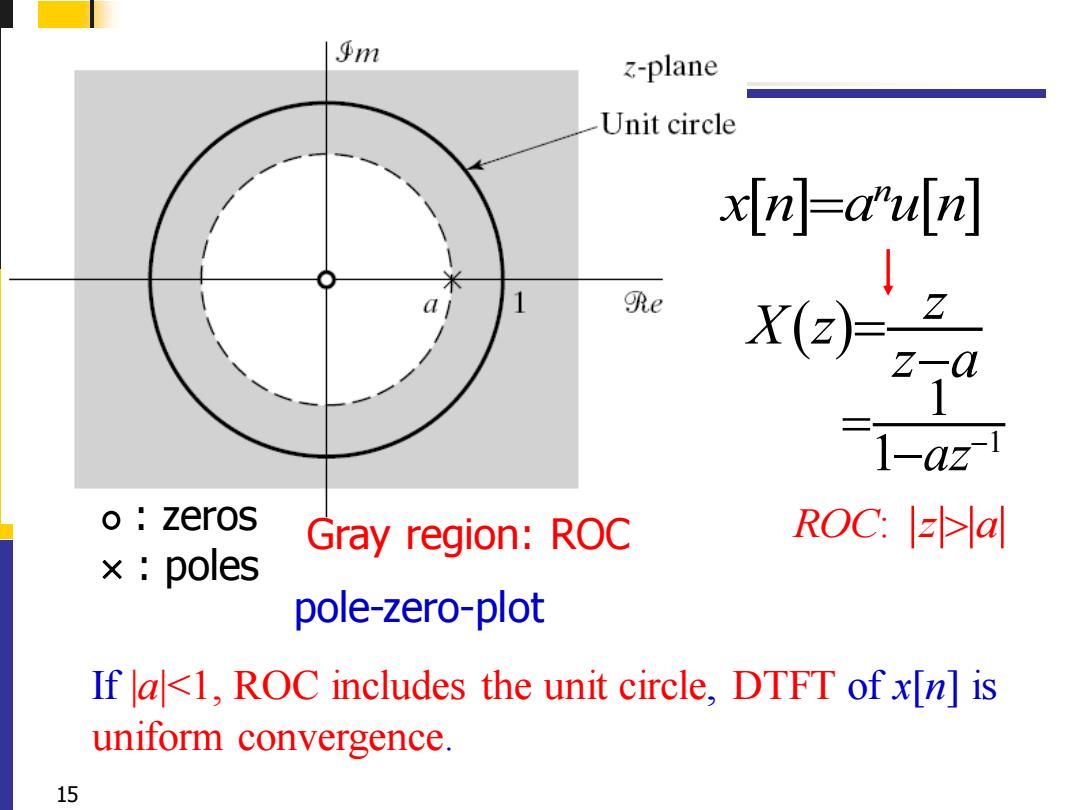
乎m z-plane Unit circle xn]=a"uln] 米 1 e z-a 1-az1 o zeros Gray region:ROC ROC:>a x poles pole-zero-plot If |a<1,ROC includes the unit circle,DTFT of x[n]is uniform convergence. 15
15 : zeros : poles Gray region: ROC n x n a u n = ( ) z X z z a = − ROC z a : 1 1 1 az = − − pole-zero-plot If |a|<1, ROC includes the unit circle, DTFT of x[n] is uniform convergence

Ex.3.2 Left-sided exponential sequence Determine the z-transform,including the ROC pole-zero-plot,for sequence: xn=-a"u-n-1] Solution: X(2)-∑4-n-2"=-∑d'z" 1-a1z z-0 Condition of convergence: Zero∶z= Roc:a'z<1,a pole:z=a 16
16 Ex. 3.2 Left-sided exponential sequence ( ) 1 1 n n n n n n X z a z u n a z − − =− − =− =− − − − = xn= −a u− n −1 n z a ( ) 1 1 1 n n n n n a z a z − − = = =− =− ◆Determine the z-transform, including the ROC, pole-zero-plot, for sequence: Solution: ROC: z z a = − : 0 : zero z pole z a = = ( ) 1 1 1 1 a z a z a z − − − − =− − 0 -1 a z1, Condition of convergence:
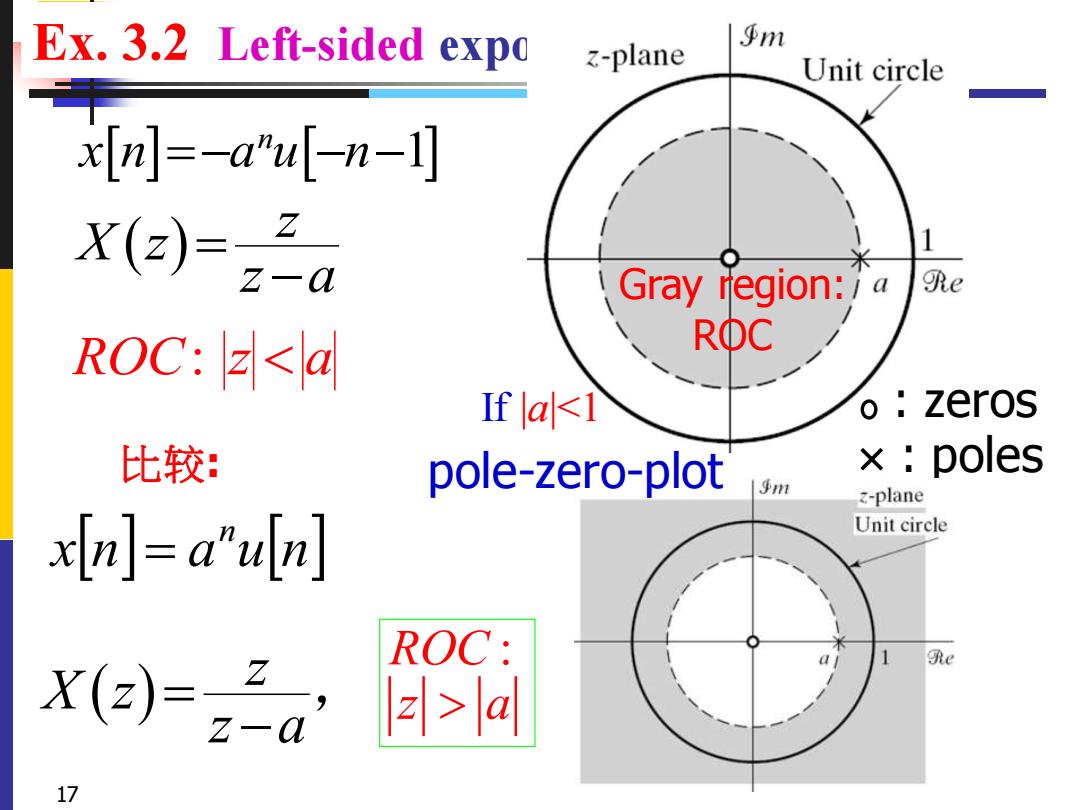
Ex.3.2 Left-sided expo 乎m 3-plane Unit circle x(n]=-a"u[-n-1] X(z) -s-a Gray region:a e ROC:<a ROC If a<l o zeros 比较: pole-zero-plot ×:poles z-plane xn]=a"uln Unit circle X(z)= ROC: Re z-a 2>a 17
Ex. 3.2 Left-sided exponential sequence 17 ( ) z X z z a = − ROC z a : 1 n x n a u n = − − − ROC : z a xn a un n = ( ) z X z z a = − , : zeros : poles Gray region: ROC 比较: pole-zero-plot If |a|<1