
第11章差错控制编玛 检错和纠错 ▣以上编码只能检测错码,不能纠正错码。例如,当接收码 组为禁用码组“100时,接收端将无法判断是哪一位码发 生了错误,因为晴、阴、雨三者错了一位都可以变成 "100”。 ·要能够纠正错误,还要增加多余度。例如,若规定许用码 组只有两个:“000”(晴),“111”(雨),其他都是禁 用码组,则能够检测两个以下错码,或能够纠正一个错码。 ▣例如,当收到禁用码组“100时,若当作仅有一个错码, 则可以判断此错码发生在“1位,从而纠正为"000” (晴)。因为“111”(雨)发生任何一位错码时都不会变 成“100这种形式。 口但是,这时若假定错码数不超过两个,则存在两种可能性: "000错一位和"111错两位都可能变成“100”,因而只 能检测出存在错码而无法纠正错码。 11
11 第11章差错控制编码 ◆ 检错和纠错 以上编码只能检测错码,不能纠正错码。例如,当接收码 组为禁用码组“100”时,接收端将无法判断是哪一位码发 生了错误,因为晴、阴、雨三者错了一位都可以变成 “100”。 要能够纠正错误,还要增加多余度。例如,若规定许用码 组只有两个:“000”(晴),“111”(雨),其他都是禁 用码组,则能够检测两个以下错码,或能够纠正一个错码。 例如,当收到禁用码组“100”时,若当作仅有一个错码, 则可以判断此错码发生在“1”位,从而纠正为“000” (晴)。因为“111”(雨)发生任何一位错码时都不会变 成“100”这种形式。 但是,这时若假定错码数不超过两个,则存在两种可能性: “000”错一位和“111”错两位都可能变成“100”,因而只 能检测出存在错码而无法纠正错码
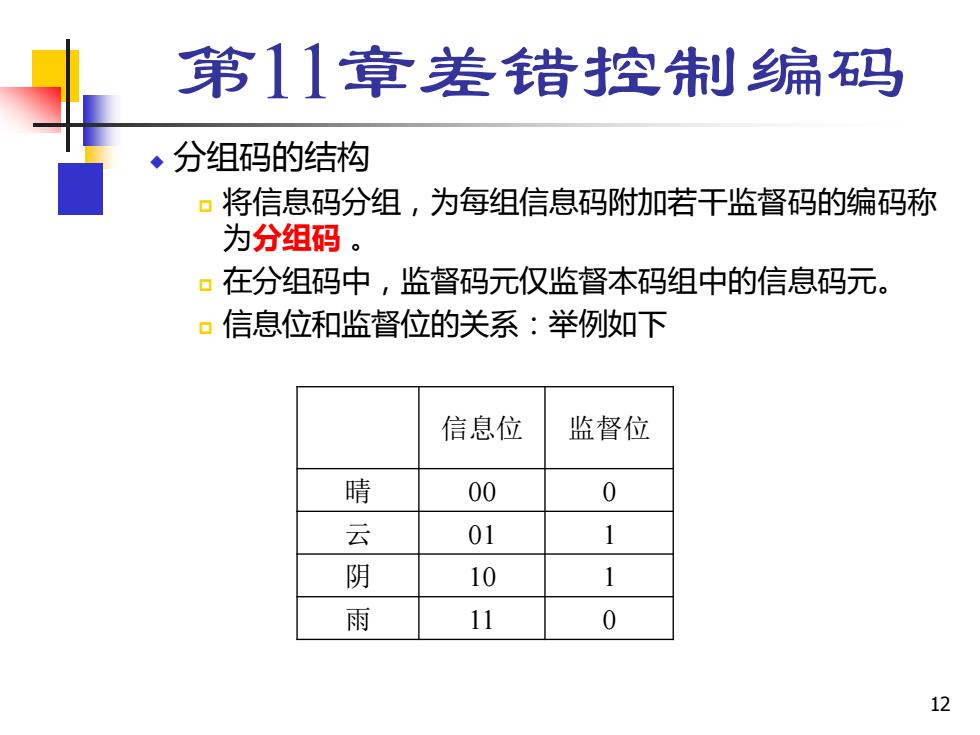
第11章差错控制编玛 ◆分组码的结构 ▣将信息码分组,为每组信息码附加若干监督码的编码称 为分组码。 口在分组码中,监督码元仅监督本码组中的信息码元。 ▣信息位和监督位的关系:举例如下 信息位 监督位 晴 00 0 云 01 1 阴 10 1 雨 11 0 12
12 第11章差错控制编码 ◆ 分组码的结构 将信息码分组,为每组信息码附加若干监督码的编码称 为分组码 。 在分组码中,监督码元仅监督本码组中的信息码元。 信息位和监督位的关系:举例如下 信息位 监督位 晴 00 0 云 01 1 阴 10 1 雨 11 0

第11章差错控制编玛 口分组码的一般结构 an-1 an-2 。●0 a, ar-1 4。 多时间 k个信息位 r个监督位 码长n=k+r ◆分组码的符号:(n,) ▣N-码组的总位数,又称为码组的长度(码长), 。k-码组中信息码元的数目, o-k=r-码组中的监督码元数目,或称监督位数目。 13
13 第11章差错控制编码 分组码的一般结构 ◆ 分组码的符号:(n, k) N - 码组的总位数,又称为码组的长度(码长), k - 码组中信息码元的数目, n – k = r - 码组中的监督码元数目,或称监督位数目

第1】章差错控制编玛 ◆分组码的码重和码距 ▣码重:把码组中“1”的个数目称为码组的重量,简称码重。 ·码距:把两个码组中对应位上数字不同的位数称为码组的 距离,简称码距。码距又称汉明距离。 口例如,“000”=晴,"011”=云,"101”=阴,“110”= 雨,4个码组之间,任意两个的距离均为2。 ▣最小码距:把某种编码中各个码组之间距离的最小值称为 最小码距(d0)。例如,上面的编码的最小码距d,=2。 14
14 第11章差错控制编码 ◆ 分组码的码重和码距 码重:把码组中“1”的个数目称为码组的重量,简称码重。 码距:把两个码组中对应位上数字不同的位数称为码组的 距离,简称码距。码距又称汉明距离。 例如,“000”=晴,“011”=云,“101”=阴,“110”= 雨,4个码组之间,任意两个的距离均为2。 最小码距:把某种编码中各个码组之间距离的最小值称为 最小码距(d0 )。例如,上面的编码的最小码距d0 = 2

第11章差错控制编玛 码距的几何意义 a 0,1,0) (1,1,0) (0,1,1 1,1,1 0,0,0) 1,0,0) "az 0,0,) 1,0,1) 。每个码组的3个码元的值(a1,a2,a3)就是此立方体各顶点的坐 标。而上述码距概念在此图中就对应于各顶点之间沿立方体 各边行走的几何距离。 ▣由此图可以直观看出,上例中4个准用码组之间的距离均为2。 15
15 第11章差错控制编码 ◆ 码距的几何意义 每个码组的3个码元的值(a1 , a2 , a3 )就是此立方体各顶点的坐 标。而上述码距概念在此图中就对应于各顶点之间沿立方体 各边行走的几何距离。 由此图可以直观看出,上例中4个准用码组之间的距离均为2。 (0,0,0) (0,0,1) (1,0,1) (1,0,0) (1,1,0) (0,1,0) (0,1,1) (1,1,1) a2 a0 a1