
二维傅里叶变换的性质: 1956 分配性和比例变换性: S[Uf1(x,y)+f2(x,y)]=S[f(x,y)]+S[f2(x,y)] af(x,y)台aF(u,v) 1 f(ax,by)台 abF(u/a.v/b)
分配性和比例变换性: 二维傅里叶变换的性质: ℑ[𝑓𝑓1(𝑥𝑥, 𝑦𝑦) + 𝑓𝑓2(𝑥𝑥, 𝑦𝑦)] = ℑ[𝑓𝑓1(𝑥𝑥, 𝑦𝑦)] + ℑ[𝑓𝑓2(𝑥𝑥, 𝑦𝑦)] 𝑎𝑎𝑎𝑎(𝑥𝑥, 𝑦𝑦) ⇔ 𝑎𝑎𝑎𝑎(𝑢𝑢, 𝑣𝑣) 𝑓𝑓(𝑎𝑎𝑎𝑎, 𝑏𝑏𝑏𝑏) ⇔ 1 𝑎𝑎𝑎𝑎 𝐹𝐹(𝑢𝑢/𝑎𝑎, 𝑣𝑣/𝑏𝑏)
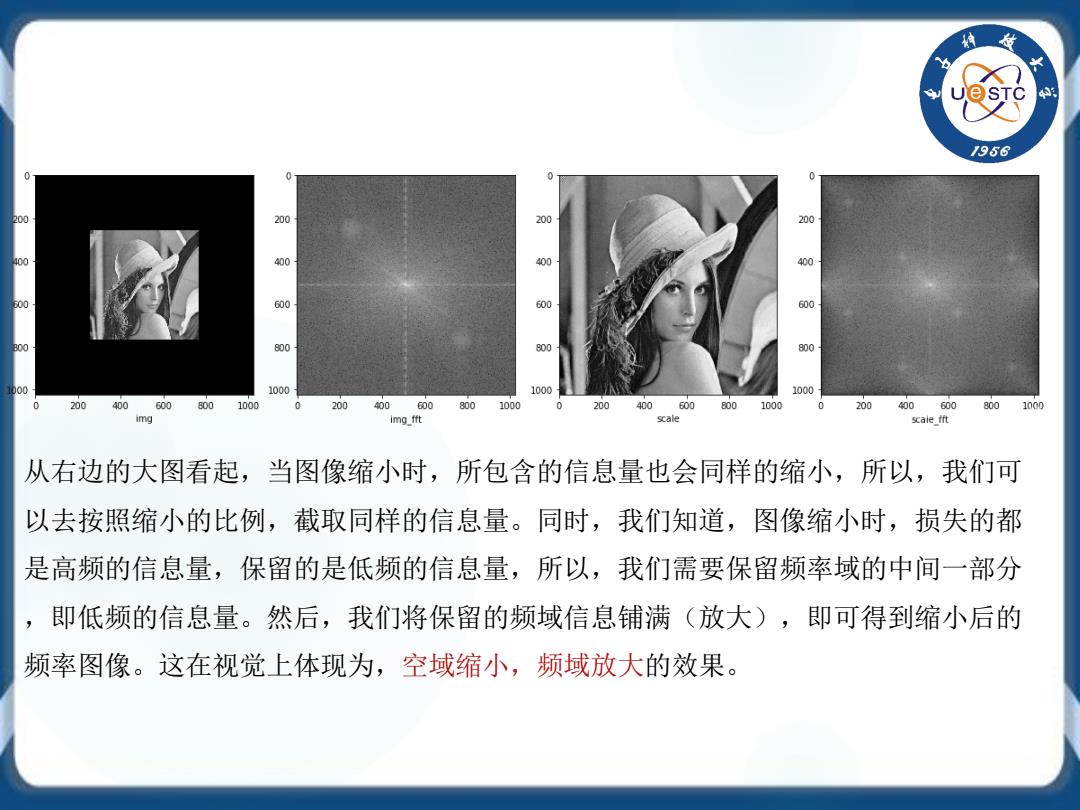
1956 00 200 200 200 400 400 600 600 200 800 800 800 100 1000 1000 1000 0 200400600 8001000 0 200 400600 800 1000 200 400E008001000 0 200 400600 800 1000 img imgf代 scale s红alet 从右边的大图看起,当图像缩小时, 所包含的信息量也会同样的缩小,所以,我们可 以去按照缩小的比例,截取同样的信息量。同时,我们知道,图像缩小时,损失的都 是高频的信息量,保留的是低频的信息量,所以,我们需要保留频率域的中间一部分 ,即低频的信息量。然后,我们将保留的频域信息铺满(放大),即可得到缩小后的 频率图像。这在视觉上体现为,空域缩小,频域放大的效果
从右边的大图看起,当图像缩小时,所包含的信息量也会同样的缩小,所以,我们可 以去按照缩小的比例,截取同样的信息量。同时,我们知道,图像缩小时,损失的都 是高频的信息量,保留的是低频的信息量,所以,我们需要保留频率域的中间一部分 ,即低频的信息量。然后,我们将保留的频域信息铺满(放大),即可得到缩小后的 频率图像。这在视觉上体现为,空域缩小,频域放大的效果

二维傅里叶变换的性质: 1956 周期性和对称性: f(x,y)=f(x+M,y)=f(x,y+N)=f(x+M,y+N) F(u,v)=F(u+M,v)=F(u,v+N)=F(u+M,v+N) F(u,)=F*(-u,-) F(u,v)=F(-u,-v)
周期性和对称性: 𝐹𝐹(𝑢𝑢, 𝑣𝑣) = 𝐹𝐹(𝑢𝑢 + 𝑀𝑀, 𝑣𝑣) = 𝐹𝐹(𝑢𝑢, 𝑣𝑣 + 𝑁𝑁) = 𝐹𝐹(𝑢𝑢 + 𝑀𝑀, 𝑣𝑣 + 𝑁𝑁) 𝐹𝐹(𝑢𝑢, 𝑣𝑣) = 𝐹𝐹∗(−𝑢𝑢, −𝑣𝑣) 𝑓𝑓(𝑥𝑥, 𝑦𝑦) = 𝑓𝑓(𝑥𝑥 + 𝑀𝑀, 𝑦𝑦) = 𝑓𝑓(𝑥𝑥, 𝑦𝑦 + 𝑁𝑁) = 𝑓𝑓(𝑥𝑥 + 𝑀𝑀, 𝑦𝑦 + 𝑁𝑁) 𝐹𝐹(𝑢𝑢, 𝑣𝑣) = 𝐹𝐹(−𝑢𝑢, −𝑣𝑣) 二维傅里叶变换的性质:
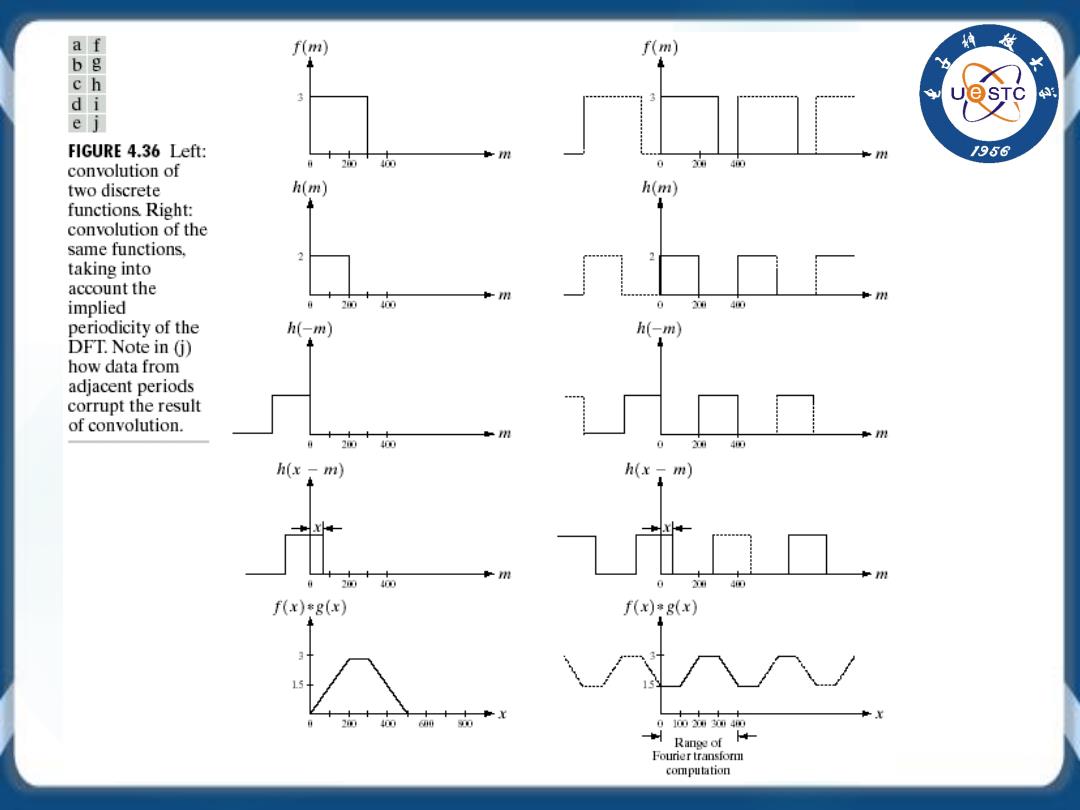
f(m) f(m) ch di ej FIGURE 4.36 Left: /956 0 40 convolution of two discrete h(m)】 h(m) functions Right: convolution of the same functions. taking into account the implied 20 400 periodicity of the h(-m》 DFT.Note in (j) how data from adjacent periods corrupt the result of convolution. 400 h(x -m) h(x-m) 40 0 f(x)*g(x) f(x)g(x) 400 0 0100030040 *制Range of Fourier transform computation

解决办法: 956 设f和h分别由A个和B个点组成,对两个函 数同时进行延拓,添加0使得它们具有相同的 周期P w- 0≤x≤A-1 A≤X≤P he()= h(x) 0≤X≤B-1 B≤X≤P 当P>=A+B-1时,卷积的两个周期才不会 发生混叠
解决办法: 设f和h分别由A个和B个点组成,对两个函 数同时进行延拓,添加0使得它们具有相同的 周期P 𝑓𝑓𝑒𝑒(𝑥𝑥) = � 𝑓𝑓(𝑥𝑥) 0 ≤ 𝑥𝑥 ≤ 𝐴𝐴 − 1 0 𝐴𝐴 ≤ 𝑥𝑥 ≤ 𝑃𝑃 ℎ𝑒𝑒(𝑥𝑥) = � ℎ(𝑥𝑥) 0 ≤ 𝑥𝑥 ≤ 𝐵𝐵 − 1 0 𝐵𝐵 ≤ 𝑥𝑥 ≤ 𝑃𝑃 当P>=A+B-1时,卷积的两个周期才不会 发生混叠