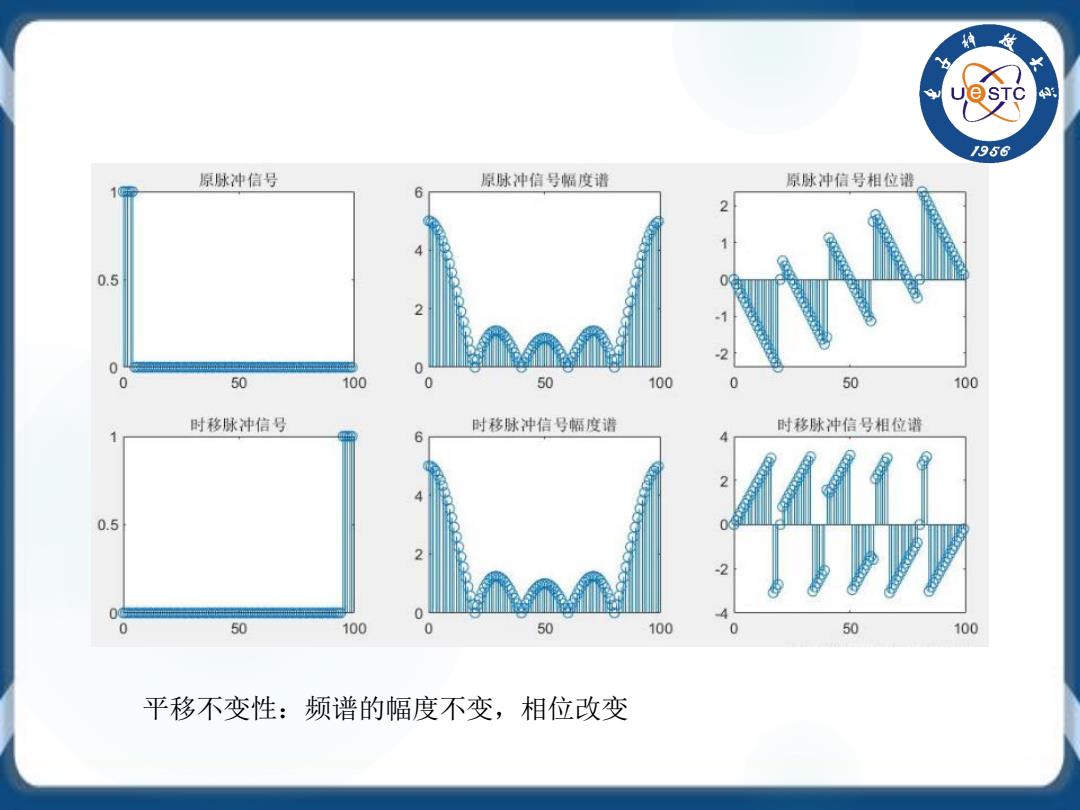
/956 原脉冲信号 原脉冲信号幅度谱 原脉冲信号相位普 6 2 0.5 2 0 50 100 0 50 100 50 100 时移脉冲信号 时移脉冲信号幅度谱 时移脉冲信号相位谱 6 4 0.5 2 0号 0 0 50 100 0 50 100 0 50 100 平移不变性:频谱的幅度不变,相位改变
平移不变性:频谱的幅度不变,相位改变

二维傅里叶变换的性质: 1956 旋转性不变性: 引入极坐标x=rcos0,y=rsin0 则有:u=ωcos中,v=ωsin中 f(r,0+0o)台F(ω,中+8o) 以角度Bo旋转f(x,y),则F(u,v)也将旋转 相同角度
旋转性不变性: 引入极坐标 则有: 以角度 𝜃𝜃0旋转f(x,y), 则F(u,v)也将旋转 相同角度. 二维傅里叶变换的性质: 𝑥𝑥 = 𝑟𝑟 cos 𝜃𝜃 , 𝑦𝑦 = 𝑟𝑟 sin 𝜃𝜃 𝑢𝑢 = 𝜔𝜔 cos 𝜙𝜙 , 𝑣𝑣 = 𝜔𝜔 sin𝜙𝜙 𝑓𝑓(𝑟𝑟, 𝜃𝜃 + 𝜃𝜃0) ⇔ 𝐹𝐹(𝜔𝜔,𝜙𝜙 + 𝜃𝜃0)

1956 ■ (a)原始图像; (b) 原始图像的傅立叶频谱: (c)旋转45°后的图像; (d)图像旋转后的傅立叶频谱
(a) 原始图像; (b) 原始图像的傅立叶频谱; (c) 旋转45°后的图像; (d) 图像旋转后的傅立叶频谱 (a) (b) (c) (d)

二维傅里叶变换的性质: 1956 可分性: M-1W-1 Fu,=∑∑f,化e2 r0u/8:x/ X=0y=0 M- W-1 1 eram∑.e X= V=0 M-1 1 M F(x,v)e-j2π(ux/M)) X=0 N-1 其中, F(x,)= ∑fx,y)e2ow/N V=0
可分性: 其中, 二维傅里叶变换的性质: 𝐹𝐹(𝑢𝑢, 𝑣𝑣) = 1 𝑀𝑀𝑀𝑀 � 𝑥𝑥=0 𝑀𝑀−1 � 𝑦𝑦=0 𝑁𝑁−1 𝑓𝑓(𝑥𝑥, 𝑦𝑦)𝑒𝑒−𝑗𝑗𝑗𝑗𝑗(𝑢𝑢𝑢𝑢/𝑀𝑀+𝑣𝑣𝑣𝑣/𝑁𝑁) = 1 𝑀𝑀 � 𝑥𝑥=0 𝑀𝑀−1 𝑒𝑒−𝑗𝑗𝑗𝑗𝑗(𝑢𝑢𝑢𝑢/𝑀𝑀) 1 𝑁𝑁 � 𝑦𝑦=0 𝑁𝑁−1 𝑓𝑓(𝑥𝑥, 𝑦𝑦)𝑒𝑒−𝑗𝑗𝑗𝑗𝑗(𝑣𝑣𝑣𝑣/𝑁𝑁) = 1 𝑀𝑀 � 𝑥𝑥=0 𝑀𝑀−1 𝐹𝐹(𝑥𝑥, 𝑣𝑣)𝑒𝑒−𝑗𝑗𝑗𝑗𝑗(𝑢𝑢𝑢𝑢/𝑀𝑀) 𝐹𝐹(𝑥𝑥, 𝑣𝑣) = 1 𝑁𝑁 � 𝑦𝑦=0 𝑁𝑁−1 𝑓𝑓(𝑥𝑥, 𝑦𝑦)𝑒𝑒−𝑗𝑗𝑗𝑗𝑗(𝑣𝑣𝑣𝑣/𝑁𝑁)
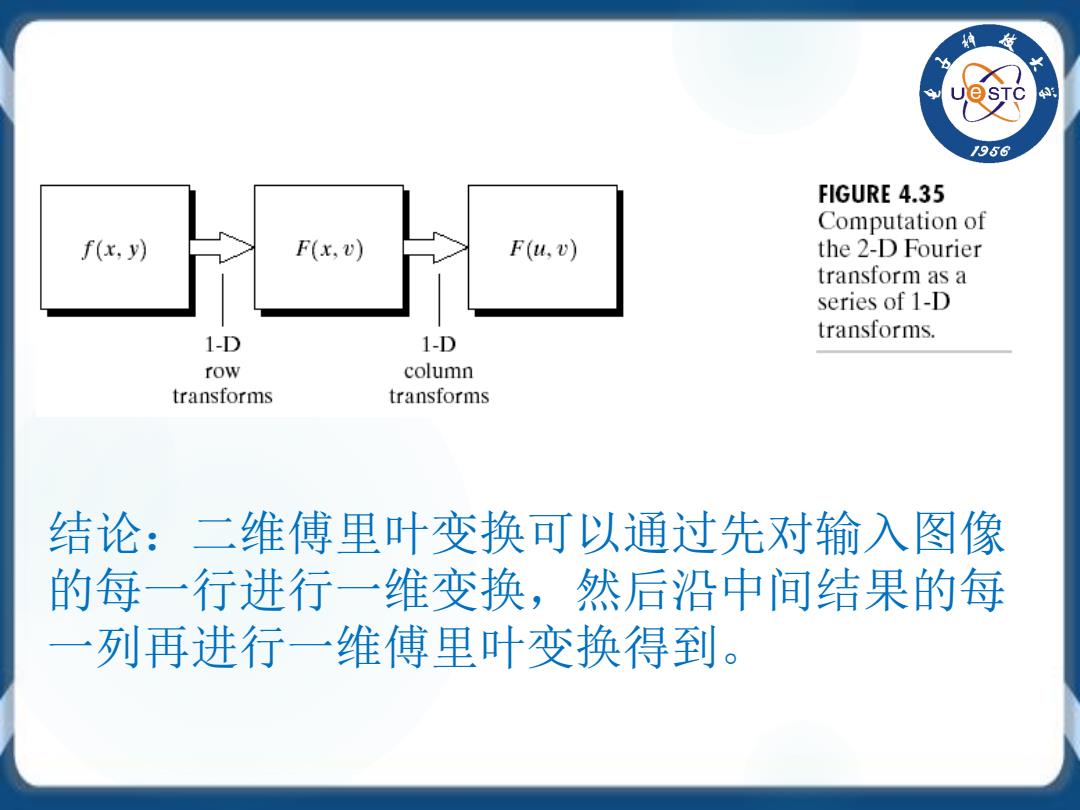
d /956 FIGURE 4.35 Computation of f(x,y) F(x,v) F(u,v) the 2-D Fourier transform as a series of 1-D transforms. 1-D 1-D row column transforms transforms 结论:二维傅里叶变换可以通过先对输入图像 的每一行进行一维变换,然后沿中间结果的每 一列再进行一维傅里叶变换得到
结论:二维傅里叶变换可以通过先对输入图像 的每一行进行一维变换,然后沿中间结果的每 一列再进行一维傅里叶变换得到