
1956 如果f(x,y)是实函数,则它的傅里叶变换 必然为对称的,即有: F(u,)=F*(-u,-) IF(u,)川=IF(-u,-)川
如果f(x,y)是实函数,则它的傅里叶变换 必然为对称的,即有: 𝐹𝐹(𝑢𝑢, 𝑣𝑣) = 𝐹𝐹∗(−𝑢𝑢, −𝑣𝑣) 𝐹𝐹(𝑢𝑢, 𝑣𝑣) = 𝐹𝐹(−𝑢𝑢, −𝑣𝑣)

二维傅里叶变换的性质: 1956 平移性: f(x,y)ej2r(uox/M+voyIN)F(u-uo,v-vo) f(x-xo,y-yo)F(u,v)e-j2m(uxo/M+vyo/N)
二维傅里叶变换的性质: 平移性: 𝑓𝑓(𝑥𝑥, 𝑦𝑦)𝑒𝑒𝑗𝑗𝑗𝑗𝑗(𝑢𝑢0𝑥𝑥/𝑀𝑀+𝑣𝑣0𝑦𝑦/𝑁𝑁) ⇔ 𝐹𝐹(𝑢𝑢 − 𝑢𝑢0, 𝑣𝑣 − 𝑣𝑣0) 𝑓𝑓(𝑥𝑥 − 𝑥𝑥0, 𝑦𝑦 − 𝑦𝑦0) ⇔ 𝐹𝐹(𝑢𝑢, 𝑣𝑣)𝑒𝑒−𝑗𝑗𝑗𝑗𝑗(𝑢𝑢𝑥𝑥0/𝑀𝑀+𝑣𝑣𝑦𝑦0/𝑁𝑁)

f(x,y)e2π(uox/M+oy/W台F(u-uo,v-vo) 1956 uo-M/2且vo=N/2时, ej2n(uox/M+voy/N)ejn(x+y)=(-1)x+y 因此有 f(x,y)(-1)x+y台F(u-M/2,v-N/2) 上式说明f(x,y)(-1)x+y的傅里叶变换 的原点u=M/2,V=N/2上
当u0=M/2且v0=N/2时, 因此有 上式说明 𝑓𝑓(𝑥𝑥, 𝑦𝑦)(−1)𝑥𝑥+𝑦𝑦 的傅里叶变换 的原点u=M/2,v=N/2上。 𝑓𝑓(𝑥𝑥, 𝑦𝑦)(−1)𝑥𝑥+𝑦𝑦 ⇔ 𝐹𝐹(𝑢𝑢 − 𝑀𝑀/2, 𝑣𝑣 − 𝑁𝑁/2) 𝑒𝑒𝑗𝑗𝑗𝑗𝑗(𝑢𝑢0𝑥𝑥/𝑀𝑀+𝑣𝑣0𝑦𝑦/𝑁𝑁) = 𝑒𝑒𝑗𝑗𝑗𝑗(𝑥𝑥+𝑦𝑦) = (−1)𝑥𝑥+𝑦𝑦 𝑓𝑓(𝑥𝑥, 𝑦𝑦)𝑒𝑒𝑗𝑗𝑗𝑗𝑗(𝑢𝑢0𝑥𝑥/𝑀𝑀+𝑣𝑣0𝑦𝑦/𝑁𝑁) ⇔ 𝐹𝐹(𝑢𝑢 − 𝑢𝑢0, 𝑣𝑣 − 𝑣𝑣0)
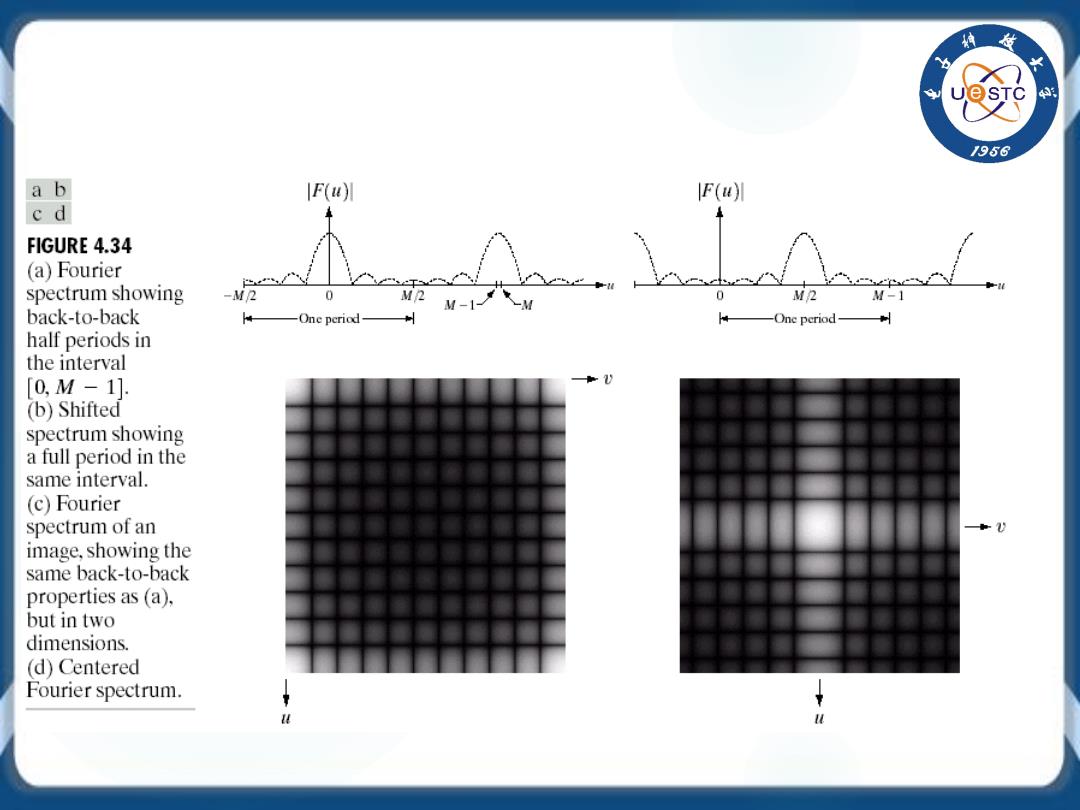
1956 a b IF(u)川 F(u cd FIGURE 4.34 (a)Fourier spectrum showing -M2 M R M-1 back-to-back -One period- -Onc period- half periods in the interval [0,M-11. (b)Shifted spectrum showing a full period in the same interval. (c)Fourier spectrum of an image,showing the same back-to-back properties as (a), but in two dimensions. (d)Centered Fourier spectrum
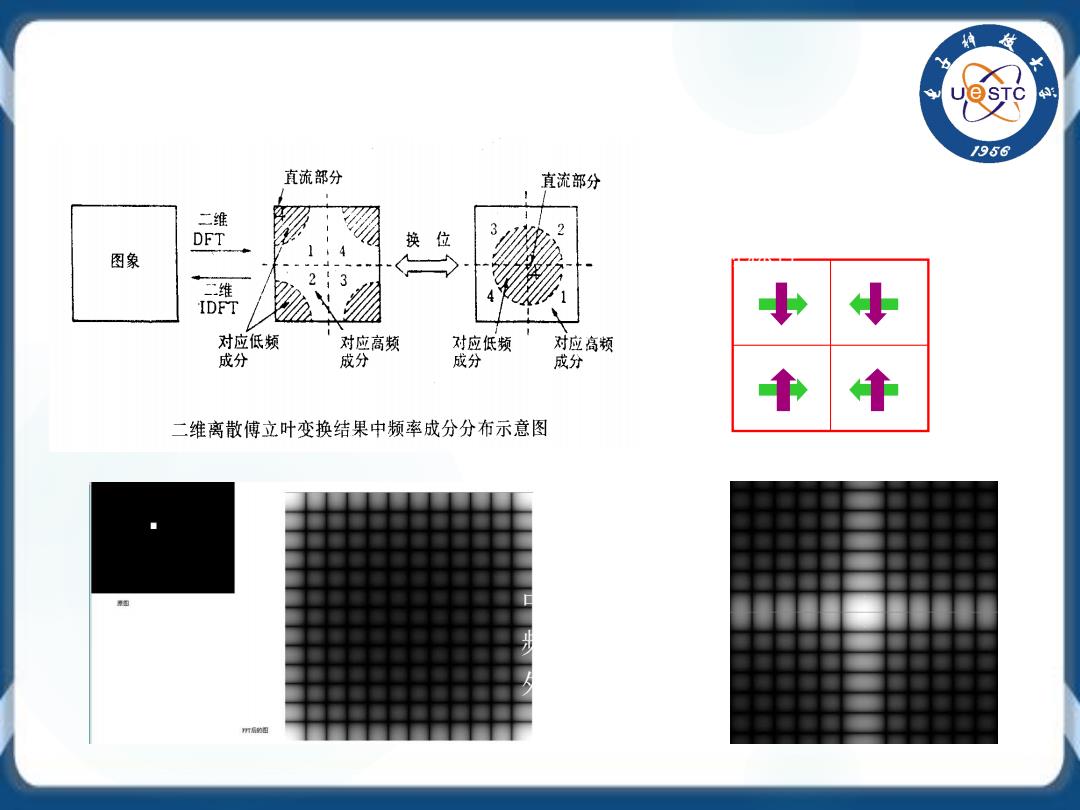
女 1956 直流部分 直流部分 维 DF 位 3 换 图象 二维 IDFT 对应低频 对应高频 对应低频 对应高频 成分 成分 成分 成分 二维离散傅立叶变换结果中频率成分分布示意图
Fuv F u v (,) ( , ) = −− 周期性 共轭对称性 F u v F u aM v bN (,) ( , ) =+ + 中间部分为低 频部分,越靠 外边频率越高