第三章卫星运动基本知识及其坐标计算 卫星运动的开普勒定律 开普勒第一定律表明,在中心 引力场中,卫星绕地球运行的轨 道面,是一个通过地球质心的静 止平面。轨道椭圆一般称开普勒 卫星绕地球运动的轨迹 椭圆,其形状和大小不变。在椭 圆轨道上,卫星离地球质心(简称 地心)最远的一点称远地点,而离 远地点P 近地点卫 地心最近的一点称近地点,它们 在惯性空间的位置也是固定不变 开普勒椭圆 的。 安藏理x大学Anhui University of Science and Technology
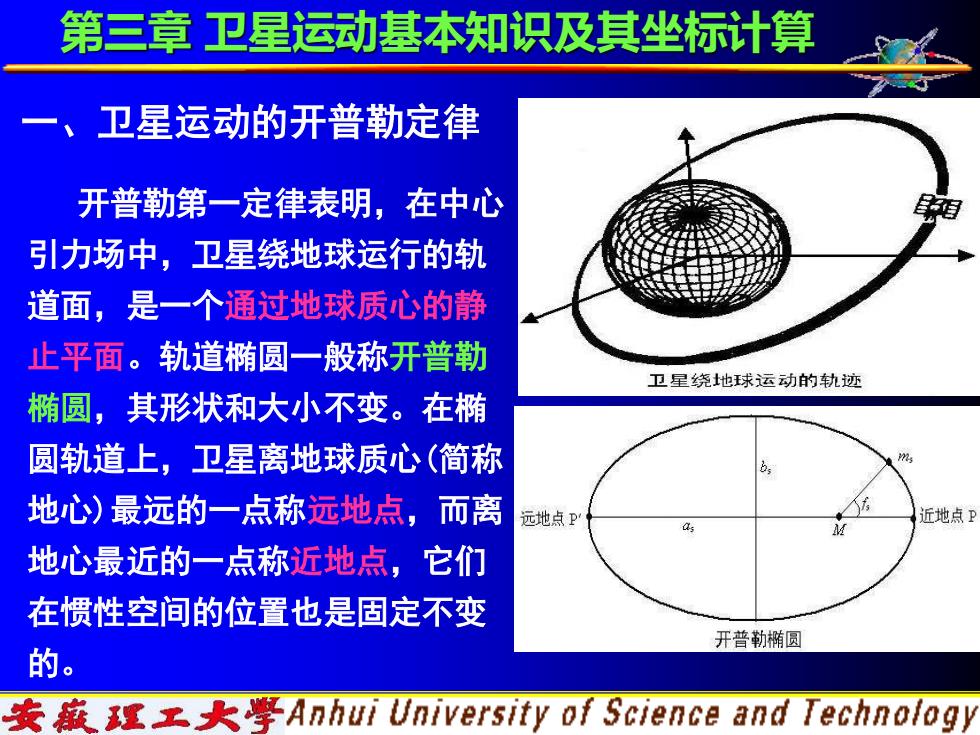
一、卫星运动的开普勒定律 开普勒第一定律表明,在中心 引力场中,卫星绕地球运行的轨 道面,是一个通过地球质心的静 止平面。轨道椭圆一般称开普勒 椭圆,其形状和大小不变。在椭 圆轨道上,卫星离地球质心(简称 地心)最远的一点称远地点,而离 地心最近的一点称近地点,它们 在惯性空间的位置也是固定不变 的。 第三章 卫星运动基本知识及其坐标计算

第三章卫星运动基本知识及其坐标计算 解式(3-2),得卫星绕地球质心运动的轨道方程: a(1-e) (3-3) 1+e.cos t 式中,为卫星的地心距离;α为开普勒椭圆的长半径, ?为开普勒椭圆的偏心率;f为真近点角,它描述了任意 时刻,卫星在轨道上,相对近地点的位置,是时间的函数 其定义如上图所示。 这一定律阐明了卫星运行轨道的基本形态及其与地心 的关系。 安骸理工大學Anhui University of Science and Technology
解式(3-2),得卫星绕地球质心运动的轨道方程: (3 3) 1 cos (1 ) 2 − + − = − r e f a e r s s s s 式中,r为卫星的地心距离;as为开普勒椭圆的长半径, es为开普勒椭圆的偏心率;fs为真近点角,它描述了任意 时刻,卫星在轨道上,相对近地点的位置,是时间的函数, 其定义如上图所示。 这一定律阐明了卫星运行轨道的基本形态及其与地心 的关系。 第三章 卫星运动基本知识及其坐标计算
第三章卫星运动基本知识及其坐标计算 2、开普勒第二定律 卫星的地心向径,即 地球质心与卫星质心间的 远地点 近地点 距离向量,在相同的时间 内所扫过的面积相等。 卫星地心向径在相同时间扫过的面积示意图 这一定律可根据(3-)式的能量积分而导出。与任何其 它的运动物体一样,在轨道上运行的卫星也具有两种能量 即位能(或势能)和动能。 安徽理工大学导航定位技术应用研究所 41 U S 余学祥(05546633378xxyu9166@aliyun.com NPTAI
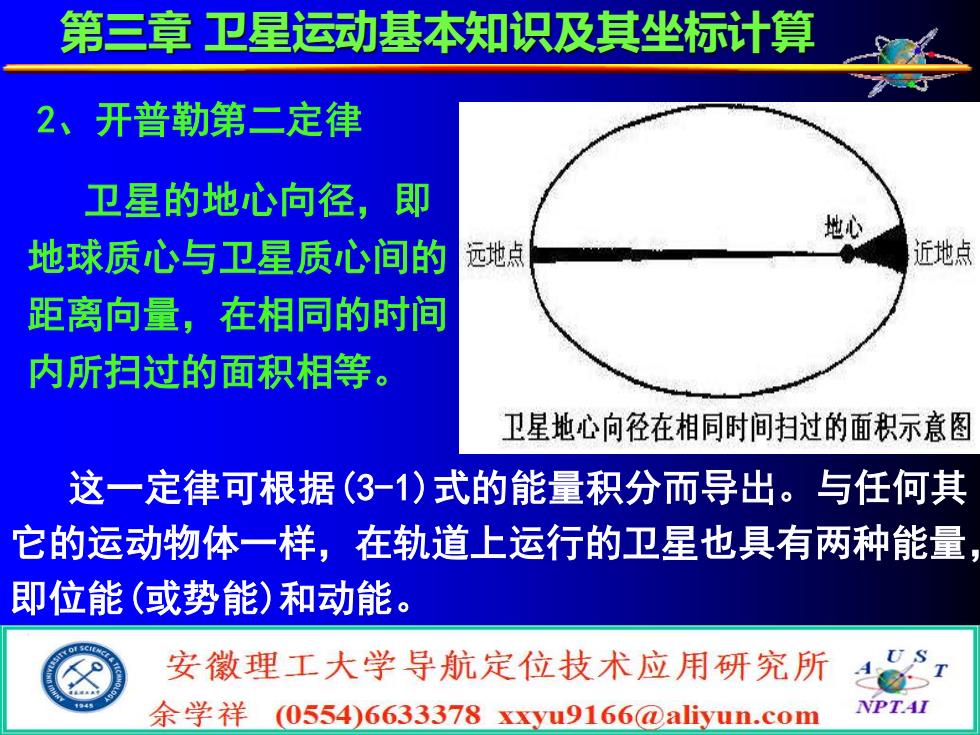
2、开普勒第二定律 卫星的地心向径,即 地球质心与卫星质心间的 距离向量,在相同的时间 内所扫过的面积相等。 这一定律可根据(3-1)式的能量积分而导出。与任何其 它的运动物体一样,在轨道上运行的卫星也具有两种能量, 即位能(或势能)和动能。 第三章 卫星运动基本知识及其坐标计算
第三章卫星运动基本知识及其坐标计算 开普勒第二定律所包含的内容是:卫星在椭圆轨道上 的运行速度是不断变化的,在近地点处速度为最大,而在 远地点时速度为最小。 S2 ti-to t2-t1 远地点 近地点 S1=S2 to 安徽理工大学导航定位技术应用研究所 U S 45 余学祥0554)6633378xxyu9166@aliyun.com NPTAI
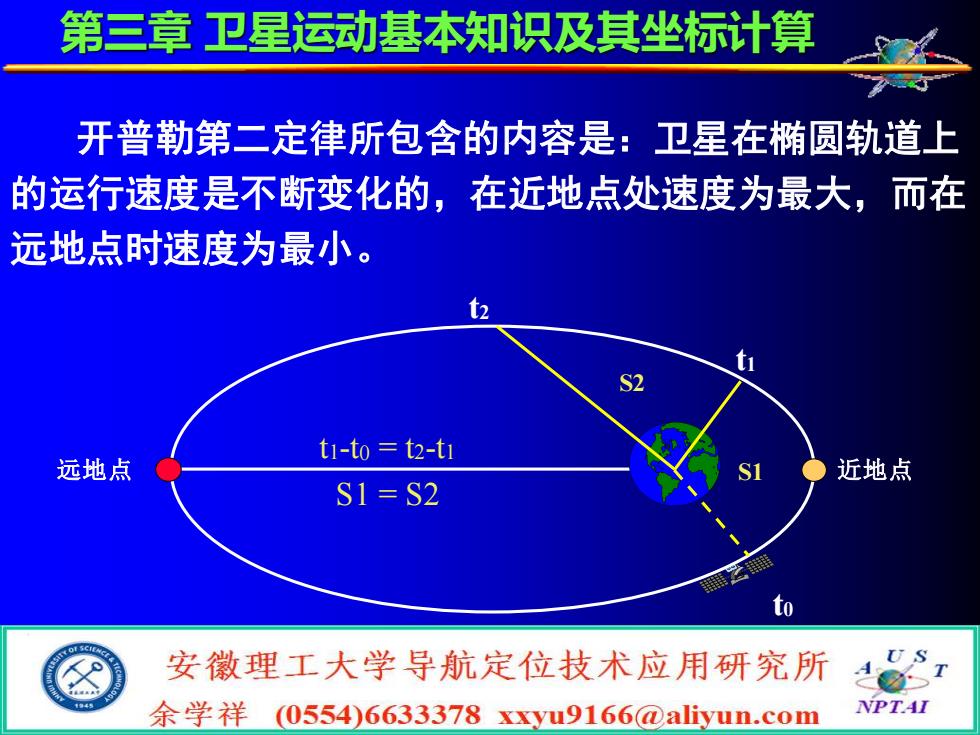
t2 S2 t0 t1 S1 t1-t0 = t2-t1 S1 = S2 远地点 近地点 开普勒第二定律所包含的内容是:卫星在椭圆轨道上 的运行速度是不断变化的,在近地点处速度为最大,而在 远地点时速度为最小。 第三章 卫星运动基本知识及其坐标计算

第三章卫星运动基本知识及其坐标计算 3、开普勒第三定律 卫星运动周期的平方与轨道椭圆长半径的立方之比为 一常量,而该常量等于地球引力常数GM的倒数。开普勒第 三定律的数学形式为 4π2 (3-4) GM 其中,T、-卫星运行周期;GM=(3986005±0.6)×108(m3/s2) 若假设卫星运动的平均角速度为n,则有 2π (radls) (3-5) T 支藏理工大学Anhui University of Science and Technology
3、开普勒第三定律 卫星运动周期的平方与轨道椭圆长半径的立方之比为 一常量,而该常量等于地球引力常数GM的倒数。开普勒第 三定律的数学形式为 (3 4) 4 2 3 2 = − a GM T s s 其中,Ts—卫星运行周期;GM=(39860050.6)108(m3 /s2) 若假设卫星运动的平均角速度为n,则有 / ) (3 5) 2 = rad s − T n s ( 第三章 卫星运动基本知识及其坐标计算