
第八章过关检测 (时间:120分钟满分:150分) 一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题 目要求的 1.己知一个四边形的直观图如图所示,其中B'C∥A'D'∥x轴,AB'∥y轴,若A'B'=2,AD=2BC-4,则原四边形的 面积为(). A.4v3 B.8V3 C.12 D.10 答案 解析由题意可知,在原四边形中,AD=4,AB=4,BC=2,故原四边形的面积为SAD+CAB=12 2.己知圆锥的底面半径为1,且它的侧面展开图是一个半圆,则这个圆锥的体积为() A B.V3π c D.5π 案A 解析设圆锥的底面半径为片,母线长为R,高为h,则2r=πR,因为r=1,所以R-2,所以h=√R2r2=√3,所以圆锥的 体积V-×12xV原= 3.己知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则 该圆柱的表面积为( ) A12V2元 B.12π C.8V2m D.10元 答案B 解析过直线O1O2的平面截该圆柱所得的截面为圆柱的轴截面,设底面半径为八,母线长为1,因为轴截面是面积 为8的正方形,所以2r=1=2VZ,即r=VZ,所以圆柱的表面积为2πl+2π2=8π+4π=12元 4.已知m,n是两条不同的直线,aB,y是三个不同的平面,则下列结论正确的是() A.若a⊥y,a⊥B,则y∥B B.若m∥n,mCa,ncB,则a∥B C.若m∥n,m∥a则n∥a D.若m∥n,m⊥an⊥B,则a∥B 答案p 解析时于A,B与y也可能相交,故A错误;对于B,a与B也可能相交,故B错误;对于C,n也可能在a内,故C错 误;对于D,m/∥n,m⊥anLa,又nLB, .a∥B,故D正确: 5.如图,在三棱柱ABC-A1BC中,侧棱AA1⊥底面A1B1C,底面三角形A1B1C1是正三角形,E是BC的中点,则下列 结论正确的是(). A.CC1与B1E是异面直线 B.AC⊥平面ABB1AI C.AE与B1C是异面直线,且AE⊥BC
第八章过关检测 (时间:120 分钟 满分:150 分) 一、选择题:本题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,只有一项是符合题 目要求的. 1.已知一个四边形的直观图如图所示,其中 B'C'∥A'D'∥x'轴,A'B'∥y'轴,若 A'B'=2,A'D'=2B'C'=4,则原四边形的 面积为( ). A.4√3 B.8√3 C.12 D.10 答案 C 解析由题意可知,在原四边形中,AD=4,AB=4,BC=2,故原四边形的面积为 S=𝐴𝐷+𝐵𝐶 2 ·AB=12. 2.已知圆锥的底面半径为 1,且它的侧面展开图是一个半圆,则这个圆锥的体积为( ). A. √3 3 π B.√3π C. √5 3 π D.√5π 答案 A 解析设圆锥的底面半径为 r,母线长为 R,高为 h,则 2πr=πR,因为 r=1,所以 R=2,所以 h=√𝑅2-𝑟 2 = √3,所以圆锥的 体积 V=1 3 π×1 2×√3 = √3 3 π. 3.已知圆柱的上、下底面的中心分别为 O1,O2,过直线 O1O2 的平面截该圆柱所得的截面是面积为 8 的正方形,则 该圆柱的表面积为( ). A.12√2π B.12π C.8√2π D.10π 答案 B 解析过直线 O1O2 的平面截该圆柱所得的截面为圆柱的轴截面,设底面半径为 r,母线长为 l,因为轴截面是面积 为 8 的正方形,所以 2r=l=2√2,即 r=√2,所以圆柱的表面积为 2πrl+2πr 2=8π+4π=12π. 4.已知 m,n 是两条不同的直线,α,β,γ 是三个不同的平面,则下列结论正确的是( ). A.若 α⊥γ,α⊥β,则 γ∥β B.若 m∥n,m⊂α,n⊂β,则 α∥β C.若 m∥n,m∥α,则 n∥α D.若 m∥n,m⊥α,n⊥β,则 α∥β 答案 D 解析对于 A,β 与 γ 也可能相交,故 A 错误;对于 B,α 与 β 也可能相交,故 B 错误;对于 C,n 也可能在 α 内,故 C 错 误;对于 D,∵m∥n,m⊥α,∴n⊥α,又 n⊥β, ∴α∥β,故 D 正确. 5.如图,在三棱柱 ABC-A1B1C1 中,侧棱 AA1⊥底面 A1B1C1,底面三角形 A1B1C1 是正三角形,E 是 BC 的中点,则下列 结论正确的是( ). A.CC1 与 B1E 是异面直线 B.AC⊥平面 ABB1A1 C.AE 与 B1C1 是异面直线,且 AE⊥B1C1
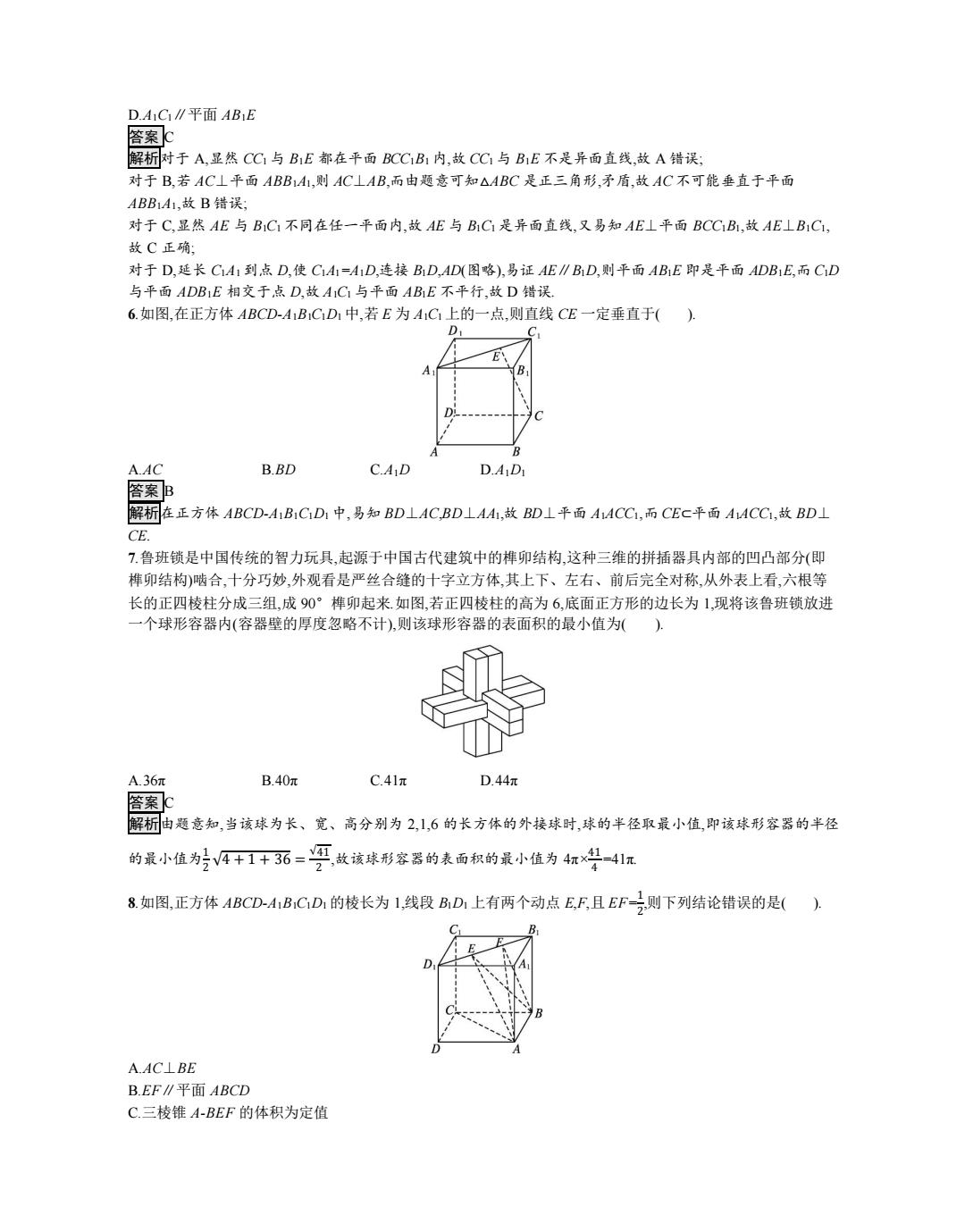
D.A1C1∥平面AB1E 答案 解析树于A,显然CC1与B1E都在平面BCC1B1内,故CC与B1E不是异面直线,故A错误; 对于B,若AC⊥平面ABB1A1,则AC⊥AB,而由题意可知△ABC是正三角形,矛盾,故AC不可能垂直于平面 ABB1A1,故B错误; 对于C,显然AE与B1C1不同在任一平面内,故AE与B1C是异面直线,又易知AE⊥平面BCCB,故AE⊥B1C1, 故C正确; 对于D,延长CA1到点D,使CA1=A1D,连接BD,AD(图略),易证AE∥BD,则平面ABE即是平面ADB1E,而C1D 与平面ADB1E相交于点D,故A1C与平面ABE不平行,故D错误 6.如图,在正方体ABCD-A1B1CD1中,若E为A1C1上的一点,则直线CE一定垂直于() D B A.AC B.BD C.AD D.AiD 答案B 解析在正方体ABCD-A1B1CD1中,易知BDLAC,BD⊥AA,故BD⊥平面A4CC,而CEC平面A4CCi,故BDL CE. 7.鲁班锁是中国传统的智力玩具,起源于中国古代建筑中的榫卯结构,这种三维的拼插器具内部的凹凸部分(即 榫卯结构)啮合,十分巧妙,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称,从外表上看,六根等 长的正四棱柱分成三组,成90°榫卯起来如图,若正四棱柱的高为6,底面正方形的边长为1,现将该鲁班锁放进 一个球形容器内(容器壁的厚度忽略不计),则该球形容器的表面积的最小值为() A.36π B.40元 C.41π D.44π 答案c 解析由题意知,当该球为长、宽、高分别为2,1,6的长方体的外接球时,球的半径取最小值,即该球形容器的半径 的最小值为V4+1+36=要故该球形容器的表面积的最小值为4红×生-41 2 4 8如图,正方体ABCD-A1B1CD1的棱长为1,线段B1D1上有两个动点E,F,且EF-二则下列结论错误的是() A.AC⊥BE B.EF∥平面ABCD C.三棱锥A-BEF的体积为定值
D.A1C1∥平面 AB1E 答案 C 解析对于 A,显然 CC1 与 B1E 都在平面 BCC1B1 内,故 CC1 与 B1E 不是异面直线,故 A 错误; 对于 B,若 AC⊥平面 ABB1A1,则 AC⊥AB,而由题意可知△ABC 是正三角形,矛盾,故 AC 不可能垂直于平面 ABB1A1,故 B 错误; 对于 C,显然 AE 与 B1C1 不同在任一平面内,故 AE 与 B1C1 是异面直线,又易知 AE⊥平面 BCC1B1,故 AE⊥B1C1, 故 C 正确; 对于 D,延长 C1A1 到点 D,使 C1A1=A1D,连接 B1D,AD(图略),易证 AE∥B1D,则平面 AB1E 即是平面 ADB1E,而 C1D 与平面 ADB1E 相交于点 D,故 A1C1 与平面 AB1E 不平行,故 D 错误. 6.如图,在正方体 ABCD-A1B1C1D1 中,若 E 为 A1C1 上的一点,则直线 CE 一定垂直于( ). A.AC B.BD C.A1D D.A1D1 答案 B 解析在正方体 ABCD-A1B1C1D1 中,易知 BD⊥AC,BD⊥AA1,故 BD⊥平面 A1ACC1,而 CE⊂平面 A1ACC1,故 BD⊥ CE. 7.鲁班锁是中国传统的智力玩具,起源于中国古代建筑中的榫卯结构,这种三维的拼插器具内部的凹凸部分(即 榫卯结构)啮合,十分巧妙,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称,从外表上看,六根等 长的正四棱柱分成三组,成 90°榫卯起来.如图,若正四棱柱的高为 6,底面正方形的边长为 1,现将该鲁班锁放进 一个球形容器内(容器壁的厚度忽略不计),则该球形容器的表面积的最小值为( ). A.36π B.40π C.41π D.44π 答案 C 解析由题意知,当该球为长、宽、高分别为 2,1,6 的长方体的外接球时,球的半径取最小值,即该球形容器的半径 的最小值为1 2 √4 + 1 + 36 = √41 2 ,故该球形容器的表面积的最小值为 4π× 41 4 =41π. 8.如图,正方体 ABCD-A1B1C1D1 的棱长为 1,线段 B1D1 上有两个动点 E,F,且 EF=1 2 ,则下列结论错误的是( ). A.AC⊥BE B.EF∥平面 ABCD C.三棱锥 A-BEF 的体积为定值

D.△AEF的面积与△BEF的面积相等 答案D 解析连接BD(图略).:在正方体ABCD-AIB1C1D1中,BB⊥平面ABCD, :AC⊥B1B,又AC⊥BD,BDnB1B=B :AC⊥平面BDD1B1,又BEC平面BDD1B1, .AC⊥BE,故A正确: ·B1D1∥BD,B1D1丈平面ABCD,BDC平面ABCD, ,B1D1∥平面ABCD :EF∥平面ABCD,故B正确; Yer青xFxB,4C是 :三棱锥A-BEF的体积为定值,故C正确: :“点A到BD,的距离与点B到BD的距离不相等,而EF是 :△AEF的面积与△BEF的面积不相等,故D不正确. 二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求全 部选对的得5分,有选错的得0分,部分选对的得2分. 9.己知a,B是两个不重合的平面,m,n是两条不重合的直线,则下列说法正确的是( ) A.若m∥n,m⊥a则n⊥a B.若m∥a,anB=n,则m∥n C.若m⊥a,m⊥B,则a∥B D.若m⊥am∥n,n⊥B,则a∥B 答案ACD 解析对于A,若m⊥a,则3a,bca且anb=P使得m⊥a,m⊥b,又m∥n,则n⊥a,nLb,由线面垂直的判定定理得n⊥ a,故A正确: D 对于B,若m∥a,anB=n,如图,设m=AB,平面AB1CD1为平面a,则m∥a,设平面ADD1A1为平面B,c∩B=A1D1=n, 则m⊥n,故B错误; 对于C,垂直于同一条直线的两个平面平行,故C正确; 对于D,若m⊥a,m∥n,则n⊥a,又n⊥B,则a∥B, 故D正确. 故选ACD, 10.如图,在长方体ABCD-A1B1CD1中,A41=AB-4,BC-2,M,N分别为棱C1D1,CC的中点,则下列说法正确的是 (). A.A,M,N,B四点共面 B.平面ADM⊥平面CDDC C.直线BW与B1M所成的角为60° D.BN∥平面ADM
D.△AEF 的面积与△BEF 的面积相等 答案 D 解析连接 BD(图略).∵在正方体 ABCD-A1B1C1D1 中,B1B⊥平面 ABCD, ∴AC⊥B1B,又 AC⊥BD,BD∩B1B=B, ∴AC⊥平面 BDD1B1,又 BE⊂平面 BDD1B1, ∴AC⊥BE,故 A 正确; ∵B1D1∥BD,B1D1⊄平面 ABCD,BD⊂平面 ABCD, ∴B1D1∥平面 ABCD, ∴EF∥平面 ABCD,故 B 正确; ∵VA-BEF= 1 3 × 1 2 EF×BB1× 1 2 AC=√2 24, ∴三棱锥 A-BEF 的体积为定值,故 C 正确; ∵点 A 到 B1D1 的距离与点 B 到 B1D1 的距离不相等,而 EF=1 2 , ∴△AEF 的面积与△BEF 的面积不相等,故 D 不正确. 二、选择题:本题共 4 小题,每小题 5 分,共 20 分.在每小题给出的选项中,有多项符合题目要求.全 部选对的得 5 分,有选错的得 0 分,部分选对的得 2 分. 9.已知 α,β 是两个不重合的平面,m,n 是两条不重合的直线,则下列说法正确的是( ). A.若 m∥n,m⊥α,则 n⊥α B.若 m∥α,α∩β=n,则 m∥n C.若 m⊥α,m⊥β,则 α∥β D.若 m⊥α,m∥n,n⊥β,则 α∥β 答案 ACD 解析对于 A,若 m⊥α,则∃a,b⊂α 且 a∩b=P 使得 m⊥a,m⊥b,又 m∥n,则 n⊥a,n⊥b,由线面垂直的判定定理得 n⊥ α,故 A 正确; 对于 B,若 m∥α,α∩β=n,如图,设 m=AB,平面 A1B1C1D1 为平面 α,则 m∥α,设平面 ADD1A1 为平面 β,α∩β=A1D1=n, 则 m⊥n,故 B 错误; 对于 C,垂直于同一条直线的两个平面平行,故 C 正确; 对于 D,若 m⊥α,m∥n,则 n⊥α,又 n⊥β,则 α∥β, 故 D 正确. 故选 ACD. 10.如图,在长方体 ABCD-A1B1C1D1 中,AA1=AB=4,BC=2,M,N 分别为棱 C1D1,CC1 的中点,则下列说法正确的是 ( ). A.A,M,N,B 四点共面 B.平面 ADM⊥平面 CDD1C1 C.直线 BN 与 B1M 所成的角为 60° D.BN∥平面 ADM

含案BC 解析树于A,显然AM,BN是异面直线,则A,M,N,B四,点不共面,故A错误: D 对于B,由题意知AD⊥平面CDD1C1,则平面ADM⊥平面CDDC,故B正确; 对于C,如图,取CD的中点O,连接BO,ON,可知三角形BON为等边三角形,则直线BN与B1M所成的角为60°, 故C正确: 对于D.BN∥平面AA1D1D.显然BN与平面ADM不平行.故D错误 11.如图①E为正方形ABCD边BC上异于点B,C的动点,将△ABE沿AE翻折,得到四棱锥B-AECD如图②所 示,且平面BAE⊥平面AECD,F为线段BD上异于点B,D的动点,则在四棱锥B-AECD中,下列说法正确的有 () 图1 图② A.直线BE与直线CF必不在同一平面上 B.存在点E使得直线BE⊥平面DCE C.存在点F使得直线CF与平面BAE平行 D.存在点E使得直线BE与直线CD垂直 答案AC 懈析树于A,假设直线BE与直线CF在同一平面上,则E在平面BCF上,又在图①冲E在线段BC上,所以E与 C重合,与E异于C矛盾,所以直线BE与直线C℉必不在同一平面上 对于B,若存在点E使得直线BE⊥平面DCE,因为AEC平面DCE,所以BE⊥AE,又AB⊥BE,所以△ABE中有两 个直角.与三角形内角和为180°矛盾,所以不存在,点E使得直线BE⊥平面DCE 对于C,取F为BD的中点,ECAD,再取AB的中点G(图略),则EC∥FG且EC=FG,所以四边形ECFG为平行 四边形,所以FC∥EG,则直线CF与平面BAE平行. 对于D,过B作BO⊥AE于O,过D作DH⊥AE于H(图略),因为平面BAE⊥平面AECD,平面BAE∩平面 AECD=AE.所以BO⊥平面AECD. 因为平面BAE⊥平面AECD.平面BAE∩平面AECD=AE,DH⊥AE,所以DH⊥平面BAE,所以DH⊥BE. 若存在,点E使得直线BE与直线CD垂直,因为DHC平面AECD,DCc平面AECD,DH∩DC=D,所以BE⊥平面 AECD,所以E与O重合,与三角形ABE是以B为直角的三角形矛盾,所以不存在,点E使得直线BE与直线CD 垂直.故选AC. 12.如图,在矩形ABCD中,M为BC的中点,将△ABM沿直线AM翻折成△AB1M,连接B1D,N为B1D的中点,则在 翻折过程中,下列说法正确的是()
答案 BC 解析对于 A,显然 AM,BN 是异面直线,则 A,M,N,B 四点不共面,故 A 错误; 对于 B,由题意知 AD⊥平面 CDD1C1,则平面 ADM⊥平面 CDD1C1,故 B 正确; 对于 C,如图,取 CD 的中点 O,连接 BO,ON,可知三角形 BON 为等边三角形,则直线 BN 与 B1M 所成的角为 60°, 故 C 正确; 对于 D,BN∥平面 AA1D1D,显然 BN 与平面 ADM 不平行,故 D 错误. 11.如图①,E 为正方形 ABCD 边 BC 上异于点 B,C 的动点,将△ABE 沿 AE 翻折,得到四棱锥 B-AECD 如图②所 示,且平面 BAE⊥平面 AECD,F 为线段 BD 上异于点 B,D 的动点,则在四棱锥 B-AECD 中,下列说法正确的有 ( ). 图① 图② A.直线 BE 与直线 CF 必不在同一平面上 B.存在点 E 使得直线 BE⊥平面 DCE C.存在点 F 使得直线 CF 与平面 BAE 平行 D.存在点 E 使得直线 BE 与直线 CD 垂直 答案 AC 解析对于 A,假设直线 BE 与直线 CF 在同一平面上,则 E 在平面 BCF 上,又在图①中 E 在线段 BC 上,所以 E 与 C 重合,与 E 异于 C 矛盾,所以直线 BE 与直线 CF 必不在同一平面上. 对于 B,若存在点 E 使得直线 BE⊥平面 DCE,因为 AE⊂平面 DCE,所以 BE⊥AE,又 AB⊥BE,所以△ABE 中有两 个直角,与三角形内角和为 180°矛盾,所以不存在点 E 使得直线 BE⊥平面 DCE. 对于 C,取 F 为 BD 的中点,EC=1 2 AD,再取 AB 的中点 G(图略),则 EC∥FG 且 EC=FG,所以四边形 ECFG 为平行 四边形,所以 FC∥EG,则直线 CF 与平面 BAE 平行. 对于 D,过 B 作 BO⊥AE 于 O,过 D 作 DH⊥AE 于 H(图略),因为平面 BAE⊥平面 AECD,平面 BAE∩平面 AECD=AE,所以 BO⊥平面 AECD. 因为平面 BAE⊥平面 AECD,平面 BAE∩平面 AECD=AE,DH⊥AE,所以 DH⊥平面 BAE,所以 DH⊥BE. 若存在点 E 使得直线 BE 与直线 CD 垂直,因为 DH⊂平面 AECD,DC⊂平面 AECD,DH∩DC=D,所以 BE⊥平面 AECD,所以 E 与 O 重合,与三角形 ABE 是以 B 为直角的三角形矛盾,所以不存在点 E 使得直线 BE 与直线 CD 垂直.故选 AC. 12.如图,在矩形 ABCD 中,M 为 BC 的中点,将△ABM 沿直线 AM 翻折成△AB1M,连接 B1D,N 为 B1D 的中点,则在 翻折过程中,下列说法正确的是( )

A.存在某个位置,使得CNLAB1 B.翻折过程中,CN的长是定值 C.若AB=BM,则AMLB1D D.若AB=BM=1,当三棱锥B1-AMD的体积最大时,三棱锥B1-AMD的外接球的表面积是4π 答案BD 图① 解桐时于A,如图O,取AD的中点为E,连接CE交MD于点F,连接NE,则NE∥AB,NF∥MB1,如果CNLAB,则 EN⊥CN,又AB1⊥MB1,则EN⊥NF,由于三线NE,NF,NC共面且共点,故CN⊥AB1不成立,A错误 对于B,如图Q∠NEC=∠MAB1=∠MAB,且NE-AB1AB,AM=EC,则在△CEN中,由余弦定理 得,NC-NE2+EC2-2 NE-EC.cos∠NEC-AB2+AP-ABAM-cos∠MAB,为定值,故NC是定值,B正确, 图② 对于C,如图②取AM的中,点O,连接B1O,D1O,因为AB=BM,即AB1=B1M所以AMLB1O,若AMLB1D,则由 B1OnB1D=B1,且B1O,B1DC平面ODB1,得AML平面ODB1,又ODC平面ODB1,所以OD⊥AM则AD=MD,由于 AD≠MD,故AM⊥B1D不成立,C错误 对于D,由题意知,当平面B1AML平面AMD时,三棱锥B1-AMD的体积最大,取AD的中,点为E,连接OE,B1E,ME, 如图② 因为AB=BM=1,所以AB1=BM=1, 且AB1⊥B1M,平面B1AM∩平面AMD=AM, 所以B1O⊥AM,又B1OC平面B1AM, 所以B1O⊥平面AMD,又OEC平面AMD, 所以BO10E,则AM=2,B04M=是 oEpM--号 从而EB1= 易知EA=ED=EM=1. 所以AD的中点E就是三棱锥B1-AMD的外接球的球心,球的半径为1,表面积是4π,故D正确
A.存在某个位置,使得 CN⊥AB1 B.翻折过程中,CN 的长是定值 C.若 AB=BM,则 AM⊥B1D D.若 AB=BM=1,当三棱锥 B1-AMD 的体积最大时,三棱锥 B1-AMD 的外接球的表面积是 4π 答案 BD 图① 解析对于 A,如图①,取 AD 的中点为 E,连接 CE 交 MD 于点 F,连接 NE,则 NE∥AB1,NF∥MB1,如果 CN⊥AB1,则 EN⊥CN,又 AB1⊥MB1,则 EN⊥NF,由于三线 NE,NF,NC 共面且共点,故 CN⊥AB1 不成立,A 错误. 对于 B,如图①,∠NEC=∠MAB1=∠MAB,且 NE=1 2 AB1= 1 2 AB,AM=EC,则在△CEN 中,由余弦定理 得,NC2=NE2+EC2 -2NE·EC·cos∠NEC=1 4 AB2+AM2 -AB·AM·cos∠MAB,为定值,故 NC 是定值,B 正确. 图② 对于 C,如图②,取 AM 的中点 O,连接 B1O,D1O,因为 AB=BM,即 AB1=B1M,所以 AM⊥B1O,若 AM⊥B1D,则由 B1O∩B1D=B1,且 B1O,B1D⊂平面 ODB1,得 AM⊥平面 ODB1,又 OD⊂平面 ODB1,所以 OD⊥AM,则 AD=MD,由于 AD≠MD,故 AM⊥B1D 不成立,C 错误. 对于 D,由题意知,当平面 B1AM⊥平面 AMD 时,三棱锥 B1-AMD 的体积最大,取 AD 的中点为 E,连接 OE,B1E,ME, 如图②. 因为 AB=BM=1,所以 AB1=B1M=1, 且 AB1⊥B1M,平面 B1AM∩平面 AMD=AM, 所以 B1O⊥AM,又 B1O⊂平面 B1AM, 所以 B1O⊥平面 AMD,又 OE⊂平面 AMD, 所以 B1O⊥OE,则 AM=√2,B1O=1 2 AM=√2 2 , OE=1 2 DM=1 2 AM=√2 2 , 从而 EB1=√( √2 2 ) 2 + ( √2 2 ) 2 =1, 易知 EA=ED=EM=1. 所以 AD 的中点 E 就是三棱锥 B1-AMD 的外接球的球心,球的半径为 1,表面积是 4π,故 D 正确