能级劈裂 据量子力学,在外加静磁场 Bo中的原子核的磁矩在空间的 ul=Yhv3 从h 4π 取向是量子化的,原子核的能 4π 量也只能是量子化的。能量E 和磁矩N关系式:E=- yh μNBo cosθ 对1H,自旋量子数I=112,这说明 自旋状态只能有两个,一个与B0平 行,一个与B0反平行。相临能级差 为AE=2μNBo
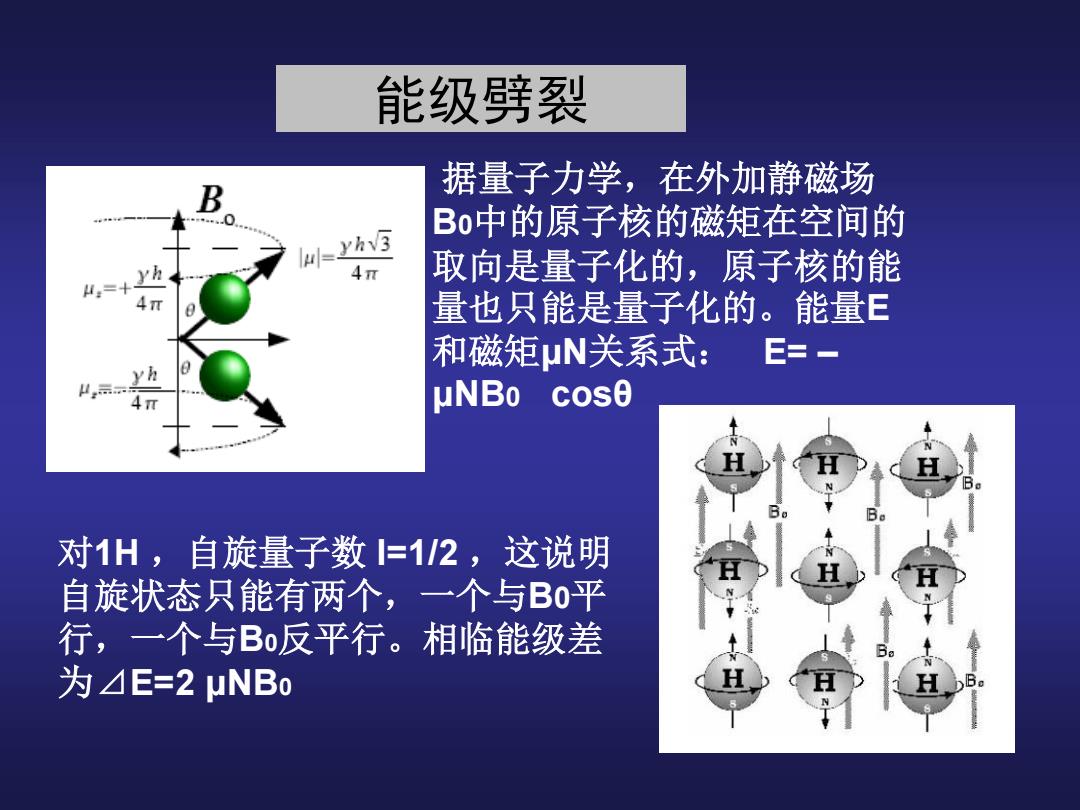
能级劈裂 据量子力学,在外加静磁场 B0中的原子核的磁矩在空间的 取向是量子化的,原子核的能 量也只能是量子化的。能量E 和磁矩μN关系式: E= – μNB0 cosθ 对1H ,自旋量子数 I=1/2 ,这说明 自旋状态只能有两个,一个与B0平 行,一个与B0反平行。相临能级差 为⊿E=2 μNB0

射频脉冲 B1为动磁场(射 频电磁场) 射频脉冲 作用:使旋进中 的原子核发生共 振跃迁 A pulse of B oscillating magnetic field at Larmor frequency B1场的强度和作用 的持续时间决定磁化 M 强度矢量M偏离Z轴 (或Bo方向)的角 度0=yB1T
射频脉冲 B1为动磁场(射 频电磁场) 作用:使旋进中 的原子核发生共 振跃迁 B1 场的强度和作用 的持续时间决定磁化 强度矢量M偏离Z轴 (或 B0方向)的角 度 1
>射频脉冲激励原子核后 磁化矢量M在XY平面中 将产生分量My, 当射频 脉冲关闭后,由于核自 uopeznaubeW 旋之间以及核自旋和晶 格之间进行能量交换产 Time Z 生纵向驰豫和横向驰豫 使得核自旋从外加射频 脉冲中吸收能量又释放 出来 Time
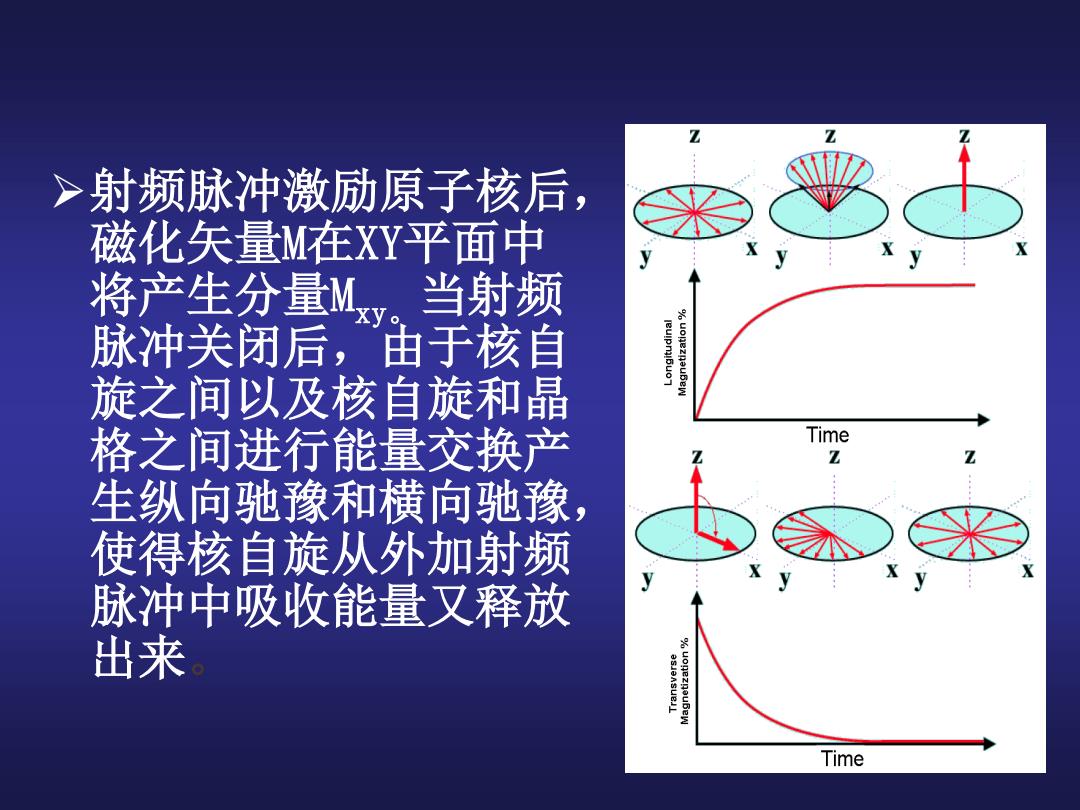
射频脉冲激励原子核后, 磁化矢量M在XY平面中 将产生分量Mxy。当射频 脉冲关闭后,由于核自 旋之间以及核自旋和晶 格之间进行能量交换产 生纵向驰豫和横向驰豫, 使得核自旋从外加射频 脉冲中吸收能量又释放 出来

磁共振物理基础 核的磁性 Bo 核的磁矩按照布郎运动原理随机取向 静止磁场内,这些磁偶极子倾向于与使用的 磁场顺向平行或逆向平行取向排列 ■ 取向与量子力学能量状态相一致,能级的实 际数目由自旋量子数)决定的 ▣自旋量子数取值士n/2(n=0,1,2,..) ▣=0,表明核没有磁矩
核的磁矩按照布郎运动原理随机取向 静止磁场内,这些磁偶极子倾向于与使用的 磁场顺向平行或逆向平行取向排列 取向与量子力学能量状态相一致,能级的实 际数目由自旋量子数I决定的 自旋量子数取值±n/2(n=0,1,2,…) n=0,表明核没有磁矩 核的磁性 磁共振物理基础
磁共振物理基础 核的磁性 M Bo 磁矩与外磁场(B。)方向不完 全一致 在外加磁场中,核自旋矢量 经历转矩作用,又称作耦合, 引起自旋以一定频率围绕外 磁场轴旋转。类似地球引力 场内的一个旋转陀螺运动, 称为拉莫尔进动 o=YB
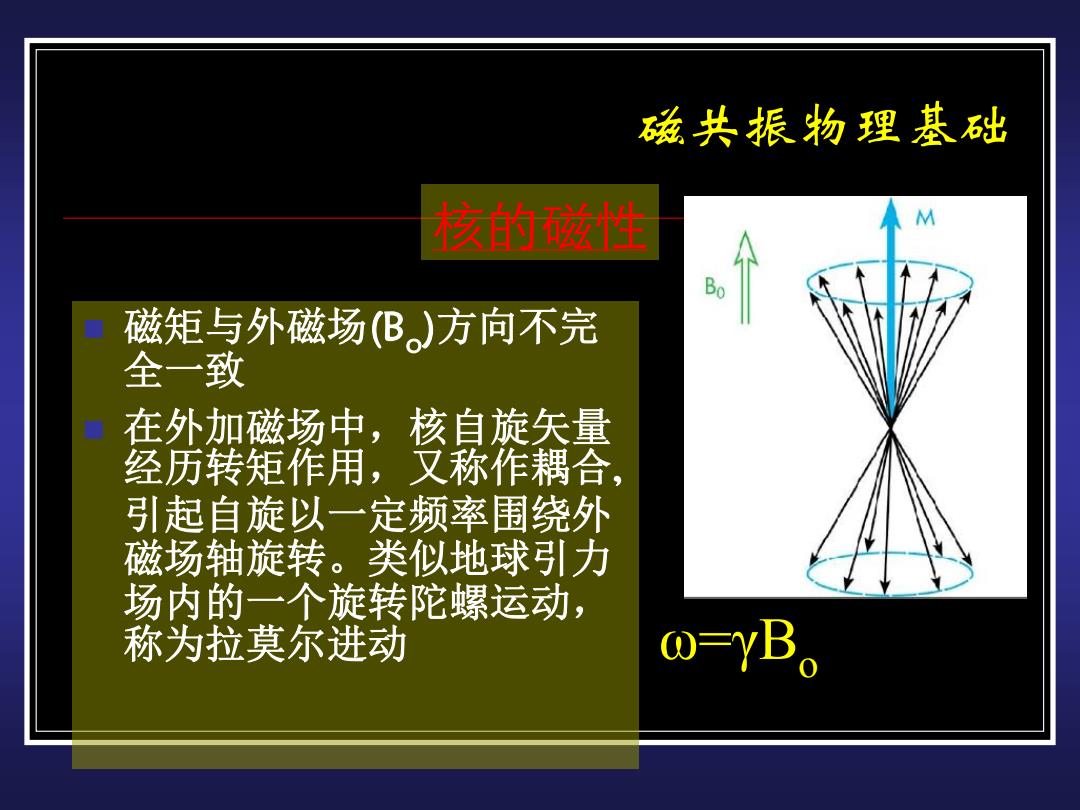
磁矩与外磁场(Bo )方向不完 全一致 在外加磁场中,核自旋矢量 经历转矩作用,又称作耦合, 引起自旋以一定频率围绕外 磁场轴旋转。类似地球引力 场内的一个旋转陀螺运动, 称为拉莫尔进动 核的磁性 ω=γBo 磁共振物理基础