
第二十二章检测 一、选择题(每小题3分,共30分) 1.将抛物线y=3x2向左平移2个单位长度,再向下平移1个单位长度,所得抛物线为 (C) Ay=3(x-2)2-1 B.y=3x-2)2+1 Cy=3(x+2)2-1 Dy=3(x+2)2+1 2.对于二次函数y=-x-1P+2的图象与性质,下列说法正确的是(B) A.对称轴是直线x=1,最小值是2 B.对称轴是直线x=1,最大值是2 C.对称轴是直线x=-1,最小值是2 D.对称轴是直线x=-1,最大值是2 3.若抛物线y=(x-m)P+(m+1)的顶点在第一象限,则m的取值范围为 (B). A.m>1 B.m>0 C.m>-1 D.-1<m<0 4.二次函数y=ax2+bx+c的图象如图所示,若点A(1,),B(2,y2)是它图象上的两点, 则y1与2的大小关系是(C) Ay1<2 B.yI=y2 Cy1>2 D.不能确定 5.己知二次函数y=x2+(m-1)x+1,当x>1时,y随x的增大而增大,则m的取值范围 是(D) A.m=-1 B.m=3 C.m<-1 D.m2-1 6某座桥桥洞的形状是一个抛物线,如图所示.该抛物线的解析式为y=x2,当水位 在AB位置时,桥洞内的水面宽为12m,此时水面离桥洞顶部的高度OC是(B)】
第二十二章检测 一、选择题(每小题 3 分,共 30 分) 1.将抛物线 y=3x 2向左平移2 个单位长度,再向下平移 1 个单位长度,所得抛物线为 (C). A.y=3(x-2)2 -1 B.y=3(x-2)2+1 C.y=3(x+2)2 -1 D.y=3(x+2)2+1 2.对于二次函数 y=-(x-1)2+2 的图象与性质,下列说法正确的是(B). A.对称轴是直线 x=1,最小值是 2 B.对称轴是直线 x=1,最大值是 2 C.对称轴是直线 x=-1,最小值是 2 D.对称轴是直线 x=-1,最大值是 2 3.若抛物线 y=(x-m) 2+(m+1)的顶点在第一象限,则 m 的取值范围为 (B). A.m>1 B.m>0 C.m>-1 D.-1<m<0 4.二次函数 y=ax2+bx+c 的图象如图所示,若点 A(1,y1),B(2,y2)是它图象上的两点, 则 y1 与 y2 的大小关系是(C). A.y1<y2 B.y1=y2 C.y1>y2 D.不能确定 5.已知二次函数 y=x2+(m-1)x+1,当 x>1 时,y 随 x 的增大而增大,则 m 的取值范围 是(D). A.m=-1 B.m=3 C.m≤-1 D.m≥-1 6.某座桥桥洞的形状是一个抛物线,如图所示.该抛物线的解析式为 y=- 1 4 x 2 ,当水位 在 AB 位置时,桥洞内的水面宽为 12 m,此时水面离桥洞顶部的高度 OC 是(B)
A.3m B.9m C.2v6 m D.4v3 m 7.函数y=ax+b和y=x2+bx+c在同一平面直角坐标系内的图象可能是下图中的 (C). D 8.老师出示了小黑板上的题后(如图所示),小华说:过点(3,0).小彬说:过点(4,3).小明 说α=1.小颖说:抛物线被x轴截得的线段长为2.你认为四人的说法中,正确的有 (C). 已知抛物线y=ax2+bx+3与x轴交于点(1,0),试添加一个条件,使它的对称轴为直线 x=2 A.1个 B.2个 C.3个 D.4个 9.下列关于二次函数y=ar2-2ar+1(a>1)的图象与x轴交点的判断,正确的是(D)】 A.没有交点 B.只有一个交点,且它位于y轴右侧 C.有两个交点,且它们均位于y轴左侧 D.有两个交点,且它们均位于y轴右侧
A.3 m B.9 m C.2√6 m D.4√3 m 7.函数 y=ax+b 和 y=ax2+bx+c 在同一平面直角坐标系内的图象可能是下图中的 (C). A B C D 8.老师出示了小黑板上的题后(如图所示),小华说:过点(3,0).小彬说:过点(4,3).小明 说:a=1.小颖说:抛物线被 x 轴截得的线段长为 2.你认为四人的说法中,正确的有 (C). 已知抛物线y=ax2+bx+3与x轴交于点(1,0),试添加一个条件,使它的对称轴为直线 x=2. A.1 个 B.2 个 C.3 个 D.4 个 9.下列关于二次函数 y=ax2 -2ax+1(a>1)的图象与 x 轴交点的判断,正确的是(D). A.没有交点 B.只有一个交点,且它位于 y 轴右侧 C.有两个交点,且它们均位于 y 轴左侧 D.有两个交点,且它们均位于 y 轴右侧

10.如图所示,抛物线y=ar2+bx+c的顶点为B(-1,3),与x轴的交点A在点(-3,0)和 (-2,0)之间,以下结论:①b2-4ac=0:②a+b+c>0:③2a-b=0:④c-a=3.其中正确的个数 是(B) A.1 B.2 C.3 D.4 二、填空题(每小题4分,共24分) 11.已知二次函数y=-x2+2x+k的部分图象如图所示,若关于x的一元二次方程 x2+2x+k=0的一个解x1=3,则另一个解x2=-1 03 12.对于二次函数y=(x-1)2+(x-32,当x=2时,函数取最小值, 13.如果函数y=ax2-ax+3x+1的图象与x轴只有一个交点,那么a的值是0或1或 9 14.将抛物线y=x2-2x向上平移3个单位长度,再向右平移4个单位长度,得到的抛 物线是y=x2-10x+27, 15.某果园有100棵橘子树,平均每棵树可收获600个橘子.根据经验估计,在此基础 上,每增种一棵树,平均每棵树就会少收获5个橘子.设果园里增种x棵橘子树,收获 橘子的总个数为y,则当果园里增种10棵橘子树时,收获橘子的总个数最多 16.若二次函数y=x2-4x+c的图象与x轴只有一个交点,则c=4 三、解答题(共96分,写出必要的文字说明、证明过程或演算步骤) 17.(8分1)请在平面直角坐标系中画出二次函数y=-x2+2x的大致图象 (2)在同一平面直角坐标系中画出y=-x2+2x的图象向上平移2个单位长度后的图 象 (3)直接写出平移后的图象的函数解析式:
10.如图所示,抛物线 y=ax2+bx+c 的顶点为 B(-1,3),与 x 轴的交点 A 在点(-3,0)和 (-2,0)之间,以下结论:①b 2 -4ac=0;②a+b+c>0;③2a-b=0;④c-a=3.其中正确的个数 是(B). A.1 B.2 C.3 D.4 二、填空题(每小题 4 分,共 24 分) 11.已知二次函数 y=-x 2+2x+k 的部分图象如图所示,若关于 x 的一元二次方程 -x 2+2x+k=0 的一个解 x1=3,则另一个解 x2= -1 . 12.对于二次函数 y=(x-1)2+(x-3)2 ,当 x= 2 时,函数取最小值. 13.如果函数 y=ax2 -ax+3x+1 的图象与 x 轴只有一个交点,那么 a 的值是 0 或 1 或 9 . 14.将抛物线 y=x2 -2x 向上平移 3 个单位长度,再向右平移 4 个单位长度,得到的抛 物线是 y=x2 -10x+27 . 15.某果园有100棵橘子树,平均每棵树可收获600个橘子.根据经验估计,在此基础 上,每增种一棵树,平均每棵树就会少收获 5 个橘子.设果园里增种 x 棵橘子树,收获 橘子的总个数为 y,则当果园里增种 10 棵橘子树时,收获橘子的总个数最多. 16.若二次函数 y=x2 -4x+c 的图象与 x 轴只有一个交点,则 c= 4 . 三、解答题(共 96 分,写出必要的文字说明、证明过程或演算步骤) 17.(8 分)(1)请在平面直角坐标系中画出二次函数 y=-x 2+2x 的大致图象. (2)在同一平面直角坐标系中画出 y=-x 2+2x 的图象向上平移 2 个单位长度后的图 象. (3)直接写出平移后的图象的函数解析式
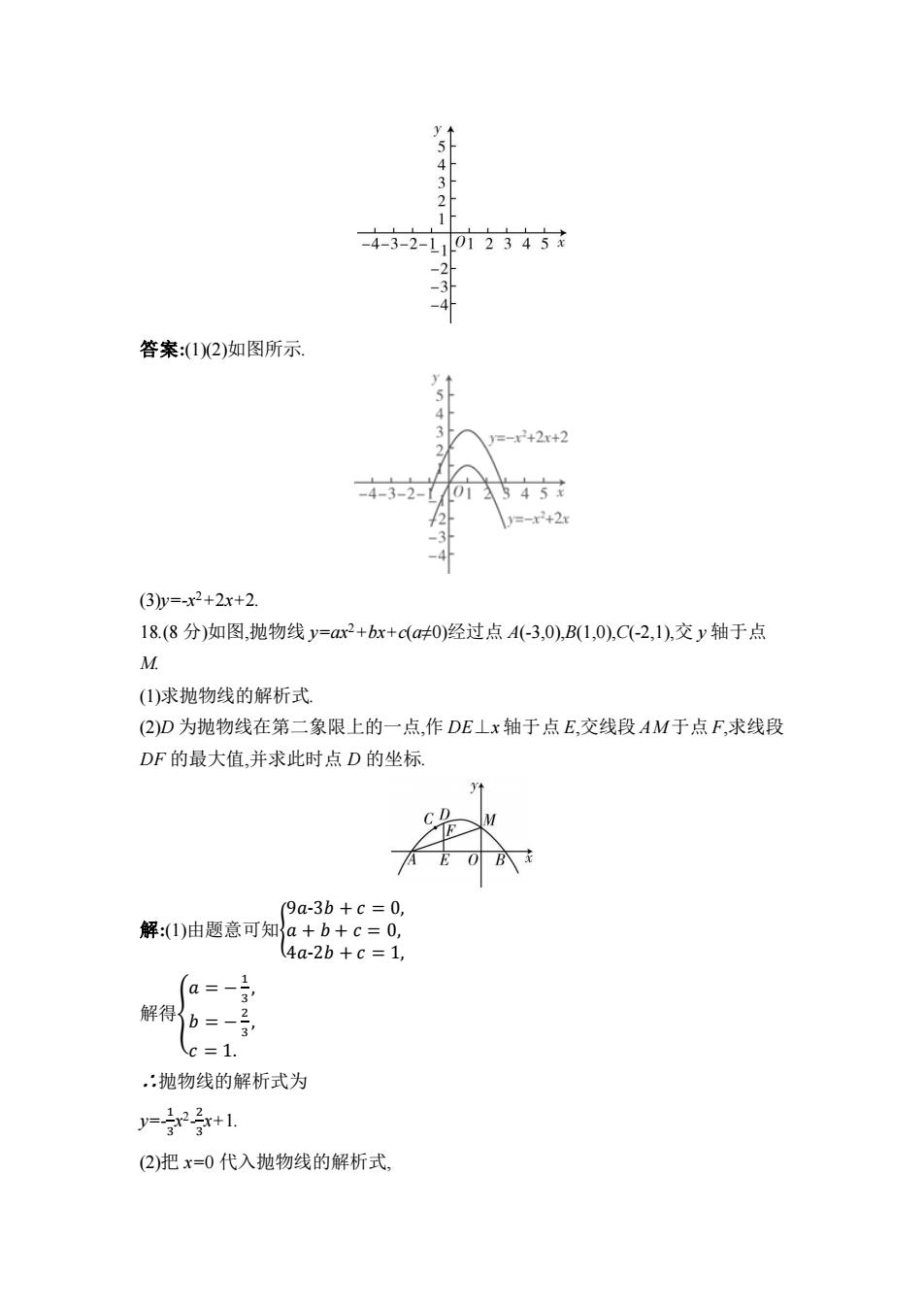
5 3 4-3-2-11 012345X -3 答案:1)2)如图所示. 4 =-2+2x+2 -4-3-2-】 01 545 1=-x2+2x 3 (3)y=-x2+2x+2. 18.(8分)如图,抛物线y=ax2+bx+c(a0)经过点A(-3,0),B(1,0),C(-2,1),交y轴于点 M (1)求抛物线的解析式 (2)D为抛物线在第二象限上的一点,作DE⊥x轴于点E,交线段AM于点F,求线段 DF的最大值,并求此时点D的坐标 9a-3b+c=0, 解:(1)由题意可知a+b+c=0, 4a-2b+c=1, (a=- 解得b=- c=1. :抛物线的解析式为 y=2号x+1 (2)把x=0代入抛物线的解析式
答案:(1)(2)如图所示. (3)y=-x 2+2x+2. 18.(8 分)如图,抛物线 y=ax2+bx+c(a≠0)经过点 A(-3,0),B(1,0),C(-2,1),交 y 轴于点 M. (1)求抛物线的解析式. (2)D 为抛物线在第二象限上的一点,作 DE⊥x 轴于点 E,交线段 AM 于点 F,求线段 DF 的最大值,并求此时点 D 的坐标. 解:(1)由题意可知{ 9𝑎-3𝑏 + 𝑐 = 0, 𝑎 + 𝑏 + 𝑐 = 0, 4𝑎-2𝑏 + 𝑐 = 1, 解得{ 𝑎 = − 1 3 , 𝑏 = − 2 3 , 𝑐 = 1. ∴抛物线的解析式为 y=- 1 3 x 2 - 2 3 x+1. (2)把 x=0 代入抛物线的解析式

得y=1. :点M的坐标为(0,1) 设直线MA的解析式为y=kx+b,则 b=1, 3k+b=0,解 k=3 (b=1. :直线MA的解析式为y=x+1. 设点D的坐标为(o,x行子o+1),则点F的坐标为oo+1) DF=吉x好号o+1o+l) =x和=0+2+星 当0=时,DF有最大值 此时x号0+1-导即点D的坐标为》 19.(10分)某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子 OA,O恰好在水面中心,安置在柱子顶端的喷头向外喷水,水流在各个方向上沿形 状相同的抛物线路径落下,且在过OA的任一平面上.抛物线形状如图①所示,如图 ②,建立平面直角坐标系,水流喷出的高度(单位:m)关于水平距离x(单位:m)的函 数解析式为y=-x2+2x+请回答下列问题: (1)柱子OA的高度为多少米?(3分) (2)喷出的水流距水平面的最大高度是多少米?(3分) (3)若不计其他因素,水池的半径至少要多少米才能使喷出的水流不至于落在池 外?(4分) 图① 图② 解(1)冷x=0,得y 故0A=m 2p=2+2x+号
得 y=1. ∴点 M 的坐标为(0,1). 设直线 MA 的解析式为 y=kx+b,则 { 𝑏 = 1, -3𝑘 + 𝑏 = 0, 解得{ 𝑘 = 1 3 , 𝑏 = 1. ∴直线 MA 的解析式为 y= 1 3 x+1. 设点 D 的坐标为(x0,- 1 3 𝑥0 2 - 2 3 x0+1),则点 F 的坐标为(x0, 1 3 x0+1). DF=- 1 3 𝑥0 2 - 2 3 x0+1-( 1 3 x0+1) =- 1 3 𝑥0 2 -x0=- 1 3 (𝑥0 + 3 2 ) 2+ 3 4 . 当 x0=- 3 2 时,DF 有最大值3 4 . 此时- 1 3 𝑥0 2 - 2 3 x0+1= 5 4 ,即点 D 的坐标为(- 3 2 , 5 4 ). 19.(10 分)某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子 OA,O 恰好在水面中心,安置在柱子顶端的喷头向外喷水,水流在各个方向上沿形 状相同的抛物线路径落下,且在过 OA 的任一平面上.抛物线形状如图①所示,如图 ②,建立平面直角坐标系,水流喷出的高度 y(单位:m)关于水平距离 x(单位:m)的函 数解析式为 y=-x 2+2x+5 4 ,请回答下列问题: (1)柱子 OA 的高度为多少米?(3 分) (2)喷出的水流距水平面的最大高度是多少米?(3 分) (3)若不计其他因素,水池的半径至少要多少米才能使喷出的水流不至于落在池 外?(4 分) 图① 图② 解:(1)令 x=0,得 y= 5 4 , 故 OA=5 4 m. (2)y=-x 2+2x+5 4