《物理化学》课程教学课件（PPT讲稿）第三章 化学势

§3.1偏摩尔量Partial/molar quantities 一、定义（ 二、偏摩尔量的物理意义 三、集合公式 G=GanA+GBnB

11 §3.1 偏摩尔量 Partial molar quantities 一、定义 二、偏摩尔量的物理意义 三、集合公式 , , C B def B B T p n G G n     =      G = GAnA+ GBnB

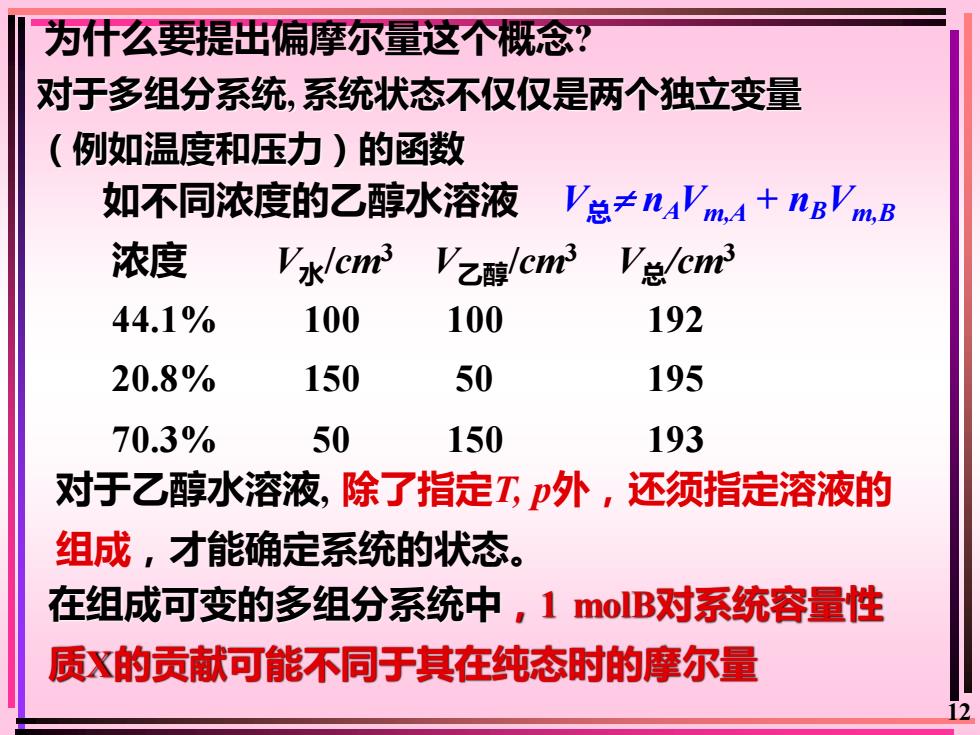
为什么要提出偏摩尔量这个不概念？ 对于多组分系统，系统状态不仅仅是两个独立变量 （例如温度和压力)的函数 如不同浓度的乙醇水溶液 V总≠nVmA+nB'mB 浓度 V水lcm3 '乙醇/cr V总/er 44.1% 100 100 192 20.8% 150 50 195 70.3% 50 150 193 对于乙醇水溶液，除了指定工，外，还须指定溶液的 组成，才能确定系统的状态。 在组成可变的多组分系统中，1oB对系统容量性 质X的贡献可能不同于其在纯态时的摩尔量

12 为什么要提出偏摩尔量这个概念? 对于多组分系统, 系统状态不仅仅是两个独立变量 （例如温度和压力）的函数 如不同浓度的乙醇水溶液 浓度 V水/cm3 V乙醇/cm3 V总/cm3 44.1% 100 100 192 20.8% 150 50 195 70.3% 50 150 193 对于乙醇水溶液, 除了指定T, p外，还须指定溶液的 组成，才能确定系统的状态。 在组成可变的多组分系统中，1 molB对系统容量性 质X的贡献可能不同于其在纯态时的摩尔量 V总 nAVm,A + nBVm,B

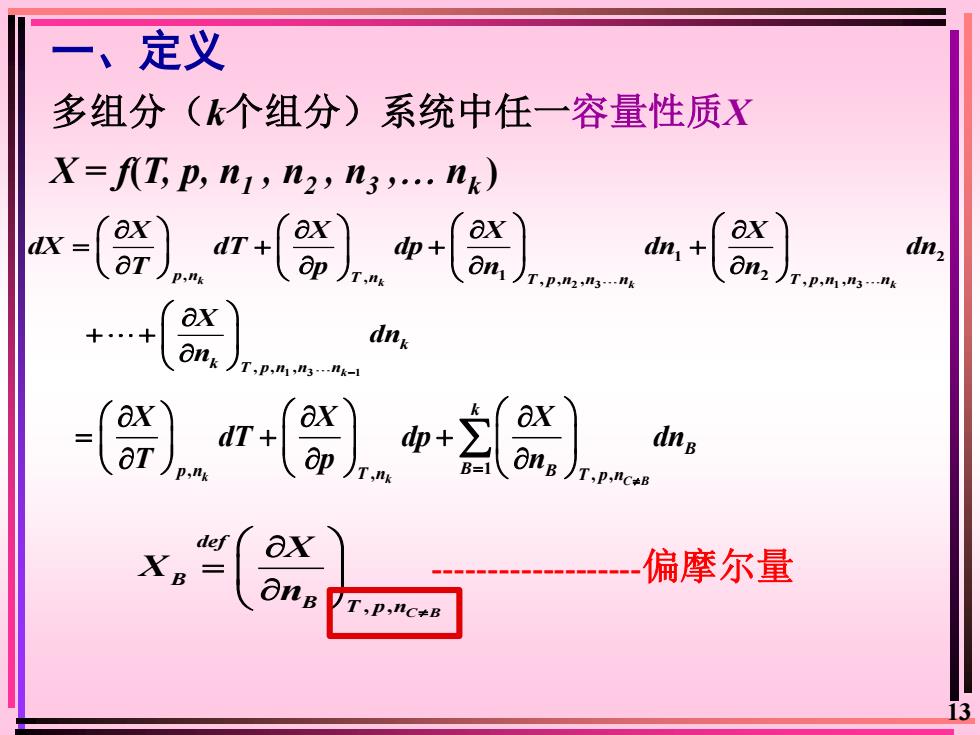
一、定义 多组分（k个组分)系统中任一容量性质X X=fT,p,n1,n2,n3.nk) ax ax dn, dnz C,P,.nk ank dn T,p,mn3-nk- p,ng Ong )T.p.nc-B dng def ax 偏摩尔量 OnB T,p,nC≠B 13

13 一、定义 多组分（k个组分）系统中任一容量性质X 2 3 1 3 1 3 1 1 2 , , 1 2 , , , , , , , , , k k k k k p n T n T p n n n T p n n n k k T p n n n X X X X dX dT dp dn dn T p n n X dn n −             = + + +                        + +     , , C B def B B T p n X X n     =      X = f(T, p, n1 , n2 , n3 , nk ) , 1 k , , , k C B k B p n T n B B T p n X X X dT dp dn T p n  =          = + +                 -偏摩尔量

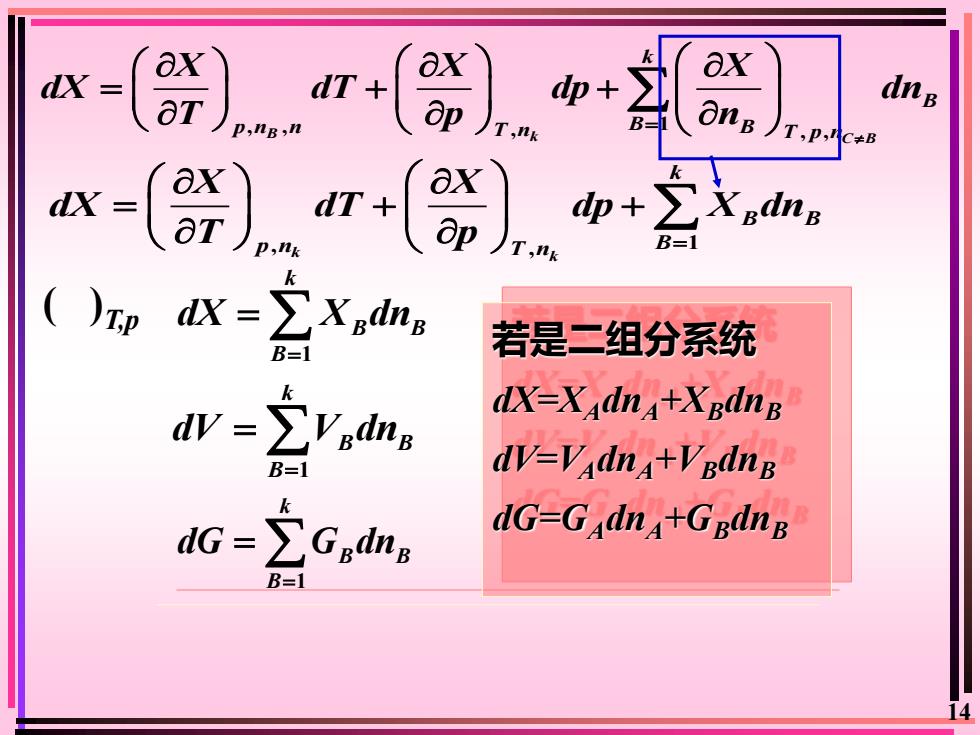
dX= dns 卫，B, C≠B dX p,nk () dX=∑Xxdrn B=1 若是二组分系统 Vadng dX-Xadna+XgdnB B=1 dV=Vadna+VpdnB dG=】 dG-Gadna+Gpdng B=1

14 , , 1 B , k , , C B k B p n n T n B B T p n X X X dX dT dp dn T p n  =          = + +                 1 k B B B dX X dn = =  1 k B B B dG G dn = =  ( )T,p , 1 k , k k B B p n T n B X X dX dT dp X dn T p =      = + +            1 k B B B dV V dn = =  若是二组分系统 dX=XAdnA+XBdnB dV=VAdnA+VBdnB dG=GAdnA+GBdnB

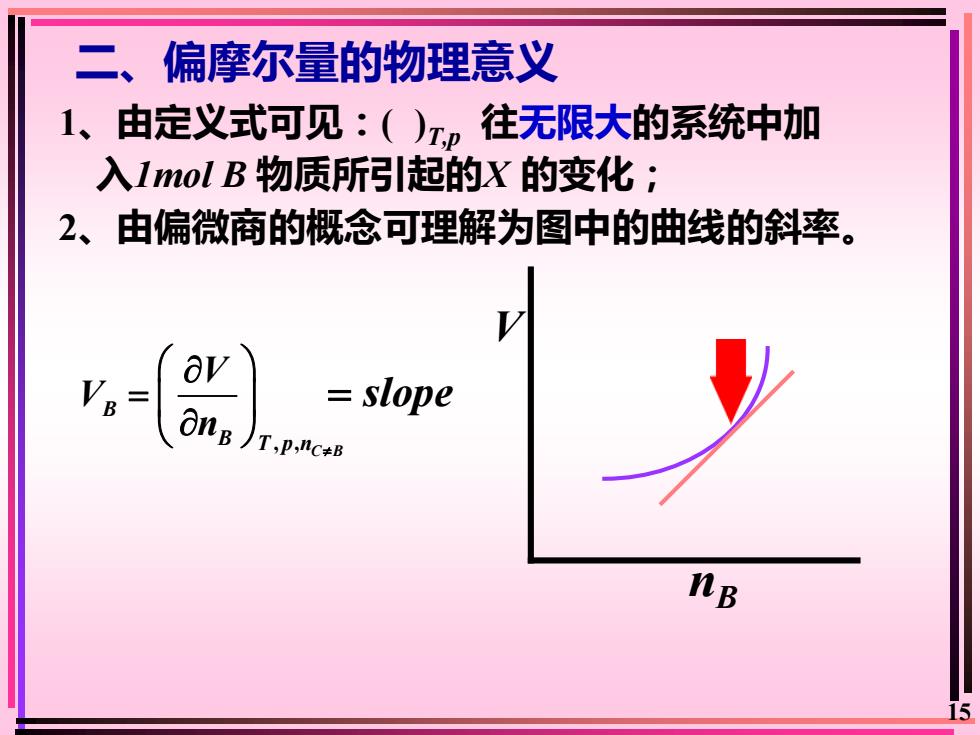
二、偏摩尔量的物理意义 1、由定义式可见：()p往无限大的系统中加 入1molB物质所引起的X的变化； 2、由偏微商的概念可理解为图中的曲线的斜率。 av VB= slope OnB )T.p. nB 15

15 二、偏摩尔量的物理意义 1、由定义式可见：( )T,p 往无限大的系统中加 入1mol B 物质所引起的X 的变化； 2、由偏微商的概念可理解为图中的曲线的斜率。 , , C B B B T p n V V n     =     V nB = slope