荷载与结构设计方法第5章 三、可靠指标B的几何意义 》 , g()=0 g()= R()=0 R(R)=0 失效域 失效城 安全嫩 安全域 图94非线性极限状态方程情况3的几何意义
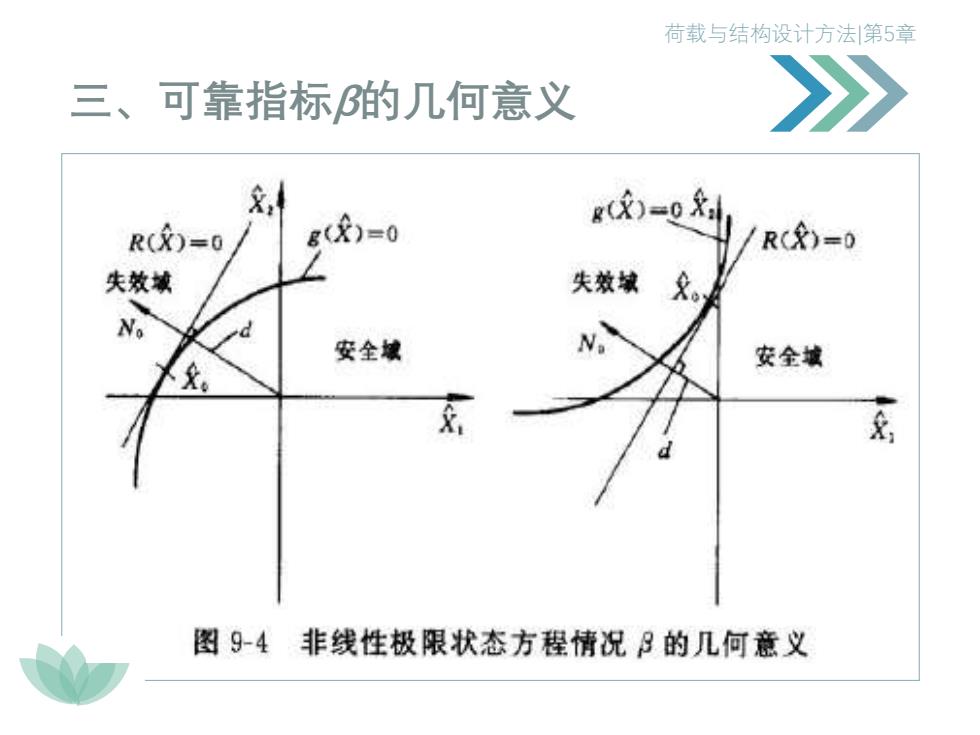
荷载与结构设计方法|第5章 三、可靠指标β的几何意义

荷载与结构设计方法第5章 三、可靠指标B的几何意义 》 1.当X=X,X,,XJT为独立正态随机向量时,可靠指 标的绝对值近似等于在标准化空间中原点到过极限状 态超曲面上某点(常取为均值点)切面的距离。 2.当X=X,X2,,XT为独立正态随机向量时,且在X的 标准化空间中极限状态曲面的最短距离代替可靠指标所 产生的误差最小
荷载与结构设计方法|第5章 三、可靠指标β的几何意义 1. 当X=[X1 , X2 ,…,Xn ] T为独立正态随机向量时,可靠指 标β的绝对值近似等于在标准化空间中原点到过极限状 态超曲面上某点 (常取为均值点) 切面的距离。 2. 当X=[X1 , X2 ,…,Xn ] T为独立正态随机向量时,且在X的 标准化空间中极限状态曲面的最短距离代替可靠指标所 产生的误差最小

荷载与结构设计方法第5章 四、中心点法的特点 》 1.直接给出B与随机变量统计参数之间的关系,计算简单; 2.对正常使用极限状态尤为适用(B=1~2); 3.没有考虑有关基本变量分布类型的信息; 4.算得的可靠指标取决于极限状态方程的形式; 5.由于在中心点处取功能函数的线性近似,由此得到的可 靠指标邓一般不为标准空间原点到极限状态曲面的最短 距离
荷载与结构设计方法|第5章 四、中心点法的特点 1.直接给出与随机变量统计参数之间的关系,计算简单; 2.对正常使用极限状态尤为适用 ( =1~2) ; 3.没有考虑有关基本变量分布类型的信息; 4.算得的可靠指标取决于极限状态方程的形式; 5.由于在中心点处取功能函数的线性近似,由此得到的可 靠指标β一般不为标准空间原点到极限状态曲面的最短 距离
荷载与结构设计方法第5章 小结 Summary (1)熟练掌握中心点法计算步骤; (2)了解可靠指标的几何意义,进一步理解可靠度 的概念: (3)了解中心点法的优缺点
荷载与结构设计方法|第5章 小结 (1)熟练掌握中心点法计算步骤; (2)了解可靠指标的几何意义,进一步理解可靠度 的概念; (3)了解中心点法的优缺点。 Summary

荷载与结构设计方法第5章 课后作业 Exercise 教材P78:S1、6
荷载与结构设计方法|第5章 课后作业 教材P78:S 1、6 Exercise