
第4客第4潮石家庄铁道学院学报vol.4a.4 199112 JOURNAL OF SHIJIAZHUANG RAILWAY INSTITUTE Dee.1991 各种不定性对中心钢压杆极限承 载力的影响及抗力不定性分析 刘嘉武 (桥梁工程系) 【摘要】本文计算了某些影响因素不定性对中心钢压杆极限承载力的影响。对钢 压杆抗力不定性分析方法作了煤讨,指出了某些方法有不尽合理之处,对怎样更合理 地确定抗力不定性提出了建议。 【关健词】机限承载力;抗力不定性:初始缺陷:变异性 1概述 彩响压杆承载力的因素很多,如:材性、截面几何特性和各种初始缺陷等(本文只讨论这几 种因素的影响)。当它们取某些定值时,对压杆稳定极限承载力的影响已有不少的研究。然而, 这些因素都是随机变量,进而导致压杆抗力的随机性。因此,有必要研究各种因索的变异对压 杆抗力的影响。我们把影响因素i的变异性用X(X=i的实际值1的标准值)表示,称为i的不 定性。由于1的不定性引起抗力的变异用K表示,称为1的不定性对抗力的影响。而综合各 仲因素的变异所引起压杆抗力的变异性用K(K=抗力实际值/抗力标准值)表示,称为抗力 不定性。本文主要讨论当X为已知的情况下,如何计算K,进而确定K。 在压杆可靠度分析中有的将压杆抗力写成如下形式] R=Rx·Xx··Ke (1) 式中Rx一一抗力标准值(按规范算得的压杆抗力): X¥ 材料强度的不定性,等于材料强度的实际值与标准值之比: X、 截面几何特性的不定性,等于截面几何特性的实际值与标准值之比: K一一计算模式的不定性」 抗力不定性KR=Xy·XA·K 收精日期1991-05-30 ·33·

这种分析方法对压杆(稳定问题)来说是不尽合理的。因为压杆抗力(弯曲失稳极限承载 力)的变化一般并非随材料强度的变化而以相同的比例变化,而是随长细比的不同而不同。 截面的几何特性的不定性对抗力的影响也是如此,所以不能认为X=K。另外,各种缺陷,如初 弯曲、初偏心,残余应力等对抗力的乾响也是随长细比的不同而不同。如用计算模式的不定性 概括它们的影响也显得粗糙。所以有必要进一步研究上述各种因素对抗力的影响。由X,求K, 进而确定K。为此,将抗力的表达式写成如下形式: R=KR·R (2) 式中RK一一抗力标准值(各种不定性因素均取其标准值时算得的极限承截力): KR一一抗力不定性,用下式表示: K=K·K·KE·K·Ke·Kg·K 其中K一一计算模式的不定性: Kv、KA,K、K、K、Kg一一分别代表材料强度,截面尺寸、弹性模量,初曲矢度、荷载偏心 和残余应力的不定性对抗力的影响,等于相应的影响因素取实际值而其他因素均取标准值时 的计算极限承载力与抗力标准值之比。如材料强度的不定性对抗力的影响为 Kr=Ry/Rx 式中R,一材料强度(截面平均屈服应力)取实际值,而其他诸影响因素均取标准值时的极 限承载力。 首先,计算各种影响K、K、…,K,然后计算抗力不定性Kw,它们都是随机变量。 以下计算中是以铁路钢桁梁常用的H形截面绕弱轴失稳为例的。截面形式见图1,截面各 组成部分的尺寸比例为 Φ=H·T/(2H·T1+B·T2)=0.345 未考虑K的变异性影响。残余应力分布图形如图」 所示,取=0.35。 在计算抗力标准值Rx时,各种不定性因素取如下标 准值: 材料屈服强度的标准值f,=340MPa, 弹性模量的标准值Ex=210GPa: 截面几何特性按截面标准尺寸计: 杆件初曲矢度的标准值Dx=1/1000(1为杆长): 图1截面形式及残余应力 荷载初偏心的标准值Cx=0.008H(H为截面高): 残余应力的标准值nf,n=0.3。 现将“曲率分段法”计算压杆极限承载力的计算方法和结果介绍如下。 2材料强度的不定性对抗力的影响Ky 材料强度不定性用X,表示,X,=屈服强度的实际值/屈服强度的标准值。参照文献[3] 的统计数据取Xy的均值xY-1.0389,标准差o×v=0.0675,变异系数Vx=0.065(16Mn)。 根据不同的X,值分别算出不同长细比情况的下极限承载力凡,进而算出与各个X,对应 。34
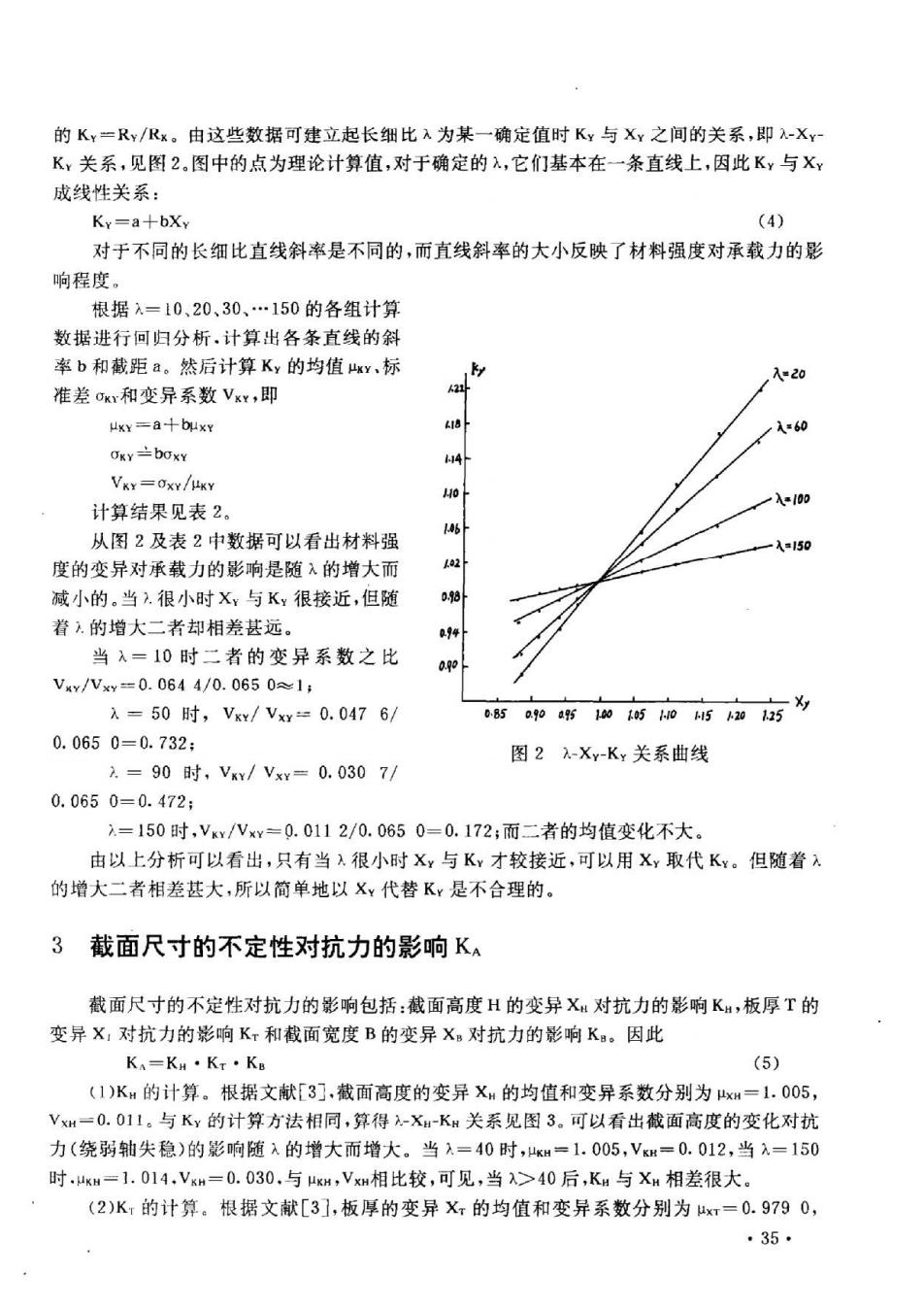
的Ky=Rv/Kx。由这些数据可建立起长细比入为某一确定值时Ky与X¥之间的关系,即-Xv K,关系,见图2图中的点为理论计算值,对于确定的入,它们基本在一条直线上,因此K,与X 成线性关系: Ky=a+bXy (4) 对于不同的长细比直线斜率是不同的,而直线斜率的大小反映了材料强度对承载力的影 响程度。 根据1=10,20、30、150的各组计算 数据进行何归分析,计算出各条直线的斜 率b和截距a。然后计算Ky的均值¥,标 20 准差w和变异系数VxY,即 uy=a+bux¥ 入60 Owy±b0xY VxY=0x/ 一入=00 计算结果见表2。 从图2及表2中数据可以看出材料强 -入=150 度的变异对承载力的影响是随入的增大而 减小的。当.很小时X¥与K¥很接近,但随 着入的增大二者却相差甚远。 94 当入=10时二者的变异系数之比 agob Vxv/Vxw=0.0644/0.0650≈1, x=50时,Vxx/Vxx=0.0476/ 脑如w烟场响5加西 0.0650=0.732: 图2λ-XyKy关系曲线 =90时,Vxx/Vx=0.0307/ 0.0650=0.472: 1=150时,Vkx/VxY=0.0112/0.0650=0.172;而二者的均值变化不大. 由以上分析可以看出,只有当人很小时Xy与K,才较接近,可以用X,取代K¥。但随着》 的增大二者相差甚大,所以简单地以X¥代替K:是不合理的。 3 截面尺寸的不定性对抗力的影响K 截面尺寸的不定性对抗力的影响包括:截面高度H的变异X对抗力的影响Ka,板厚T的 变异X,对抗力的影响K和截面宽度B的变异X,对抗力的影响K。因此 KA=KH·Kr·KB (5) (1)KH的计算。根据文献[3],截面高度的变异Xw的均值和变异系数分别为xw=1.005 Vxm=0.O11。与Ky的计算方法相同,算得X-KH关系见图3。可以看出截面高度的变化对抗 力(绕弱轴失稳)的影响随入的增大而增大。当入=40时,m=1.005,Vm=0.012,当入=150 时x=1.014.Vx4=0.030,与xm,Vxm相比较,可见,当>40后,KH与XH相差很大。 (2)K的计算。根据文献[3],板厚的变异X的均值和变异系数分别为x=0.9790, ·35·
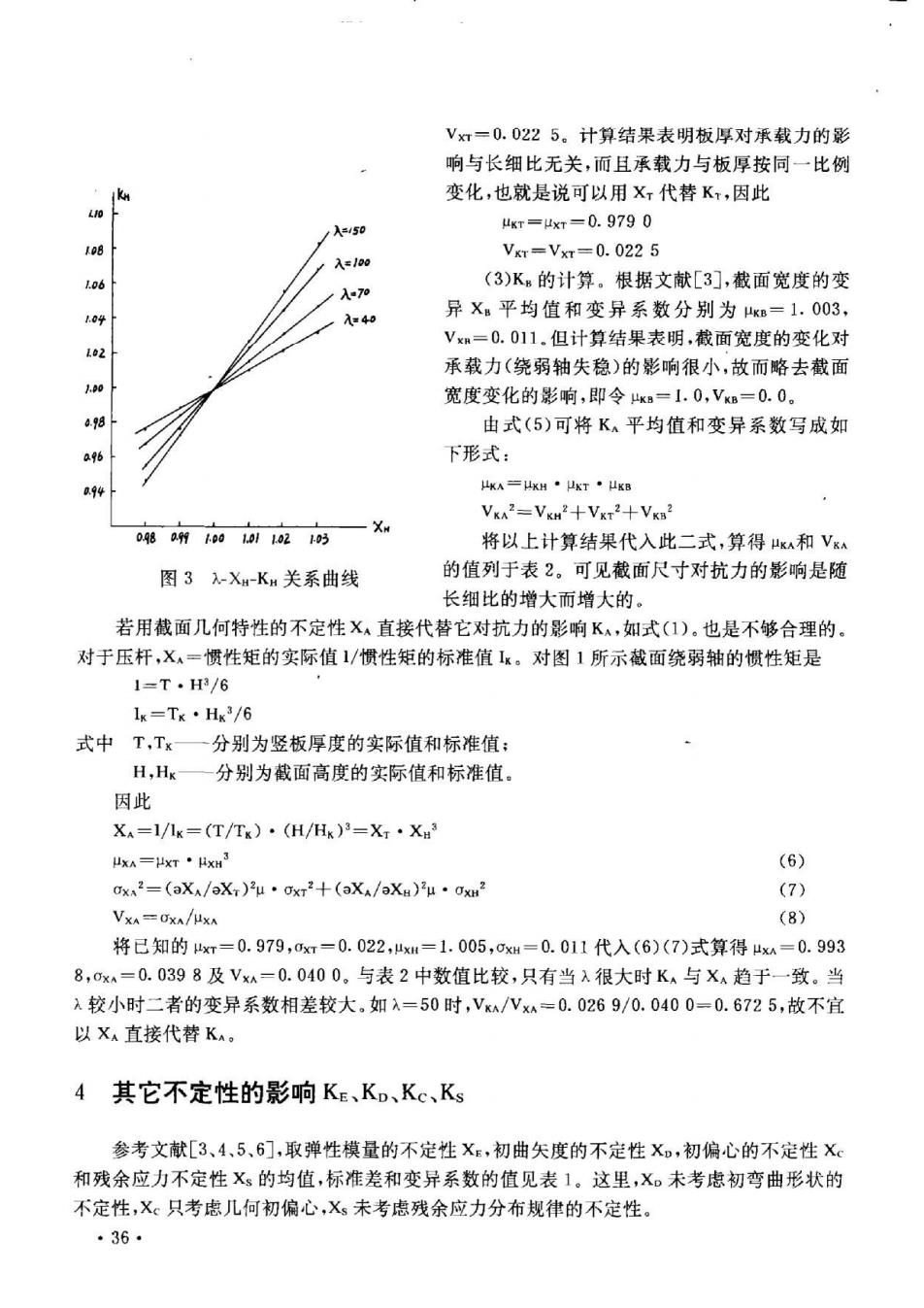
Vx灯=0.0225。计算结果表明板厚对承载力的影 响与长细比无关,而且承载力与板厚按同一比例 变化,也就是说可以用X,代替K,因此 uKr=ur=0.9790 /A=50 A=loo VxT=Vx灯=0.0225 A-70 (3)K的计算。根据文献[3],截面宽度的变 4 异X。平均值和变异系数分别为B=1.003, Vxm=0.011.但计算结果表明,截面宽度的变化对 承载力(绕弱轴失稳)的影响很小,故而略去截面 宽度变化的影响,即令w-1.0,Vk=0.0。 48 由式(5)可将K、平均值和变异系数写成如 % 下形式: =4H·k灯· VxA=VKH2+Vxt2+VKB2 将以上计算结果代入此二式,算得xA和Vx 图3XM-Km关系曲线 的值列于表2,可见截面尺寸对抗力的影响是随 长细比的增大而增大的。 若用截面几何特性的不定性X直接代替它对抗力的影响K,如式(1)。也是不够合理的, 对于压杆,X=惯性矩的实际值1/惯性矩的标准值k。对图1所示被面绕弱轴的惯性矩是 1=T.H/6 lk=Tx·Hw3/6 式中T,Tx一分别为竖板厚度的实际值和标准值: H,Hx 分别为截面高度的实际值和标准值, 因此 XA=1/1g=(T/Tg)·(H/Hk)3=Xx·X (6) oka2=(aX/oX)u·ox2+(oX/Xa)u·02 (7) VxA=Oxn/x (8) 将已知的x=0.979,0=0.022,=1.005,ox=0.011代入(6)(7)式算得=0.993 8,0xA=0.0398及Vx-0.0400。与表2中数值比较,只有当入很大时K与X趋于一致。当 较小时二者的变异系数相差较大.如=50时,V/Vx=0.0269/0.0400=0.6725,故不宜 以X直接代替K 4其它不定性的影响KE、Ko、Kc、Ks 参考文献[3、4、5、6],取弹性模量的不定性X:,初曲矢度的不定性X。,初偏心的不定性X 和残余应力不定性X的均值,标准差和变异系数的值见表1。这里,X。未考虑初弯曲形状的 不定性,X只考感儿何初偏心,X未考感残余应力分布规律的不定性。 .36
表1X、X知,Xc,Xs统计参数 XE X X X 0.9952 0.7130 0.4625 1.0000 0.0296 0.1110 0.3588 0.2260 0.0298 0.1550 0.7757 0.2260 算得各个K值的均值和变异系数列于表2。计算方法与K、K相同,不再详述。 从计算结果看,弹性模量的变异对系载力的影响随入 增大而增大当入较小时对承载力 几乎没有影响。而X,X,Xs对抗力的影响则在中等长细比时最大。 5抗力不定性K的确定 抗力不定性可由公式(3)计算 KR=Ky·Ka·KE·KD·Ke·Ks·Ke 式中K。为计算模式的不定性。根据文献[4门焊接H形压杆的实验数据确定=1.1163, V=0.0256。这里暂未考虑承载能力的计算 直与规范值的差异 当KK….K。相互独立时,根据式(3)可按下式计算抗力不定性的均值和变异系数 g一k¥·gA·μxE·μKD·xC·μs·gP VxP2=VxY:+VKa2+VKE2+VKD2+Vxc2+Vx52+Vx 计算结果列于表2。 由表2中计算结果可以发现,各种不定性对抗力的影响随入的不同变化很大,但是,由于 它们的变化趋势不同(有的随入的增大而增大,有的随入的增大而减小,有的中等长细比时较 大而其他情况较小),使得总的抗力不定性K.随入的不同变化并不很大。为了检验这种变化对 压杆可靠度的影响程度。以铁路钢析梁压杆为例计算了各种长细比情况下的可靠指标B(列于 表2) 在=30一150范围内B值变化并不很大, 6.0784(=110),B 5.83051 30). 者相差0.2479,为4.1%,若用各种入时和Vu的平均值u和V作为代表值,算得 的可常指标B-5.9621,与相差0.1163,为2.0%.与Bn相差0.1318,为2.2%。可见用 R和Vx作为各种长细比时抗力不定性的代表值所引起误差不大。B值随入的变化情况及百见 图4。 市西动如的如0前物加加西加加肉入 图4B值随人的变化及其平均值B ·37