
刚才我们提到的最常见的概率密度函数是正态分布是什么意思?我们还是 通过一个例子来说明。血液中GH-5是一种衡量人们健康水平的指标,GH-5水 平明显高于平均水平的人,一般来说健康是有问题的。我们假设John做了化验, 他的GH-5的水平是65,而健康人的GH-5的平均水平为50,标准差为25。这 个水平在不同的人群中可能会有一些变化,也就是说所有人的平均值是50,标 准差是25,但是具体到每一个人身上,它会在这个范围内有一些小的变化。我 们的问题是,John的GH-5水平是65,相对于平均水平为50标准差为25的 GH5的概率分布来说,John有没有问题?很显然,我们先要看一看世界上其他 人群的分布情况,根据GH-5水平的分布情况来判断John是否是健康的。按照 平均值为50,标准差为25,我们可以给出一个概率密度函数的曲线,它表示了 GH-5在世界范围内的分布情况,它符合正态分布。 p(x)=exp (x-2 2G2 正态分布的概率密度函数在画出来之后是一个类似钟型的连续分布。这个钟 型的形状,包括它的高低和胖瘦是由平均值和标准差来定义的。所以我们刚才提 到了GH-5的平均值是50,标准差是25。在任何一个点上,GH-5的任何一个 取值的概率就可以通过上面的公式计算得到。 除了GH-5符合正态分布之外,其他很多现象也都符合正态分布。或者我们 可以理解为当数据的样本数非常大的时候,它的分布基本上就符合正态分布。 某个事件在某个取值范围内发生的概率就是这条曲线在这个取值范围内围
刚才我们提到的最常见的概率密度函数是正态分布是什么意思?我们还是 通过一个例子来说明。血液中 GH-5 是一种衡量人们健康水平的指标, GH-5 水 平明显高于平均水平的人,一般来说健康是有问题的。我们假设 J瀂濻瀁 做了化验, 他的 GH-5 的水平是 65,而健康人的 GH-5 的平均水平为 50,标准差为 25。这 个水平在不同的人群中可能会有一些变化,也就是说所有人的平均值是 50,标 准差是 25,但是具体到每一个人身上,它会在这个范围内有一些小的变化。我 们的问题是,J瀂濻瀁 的 GH-5 水平是 65,相对于平均水平为 50 标准差为 25 的 GH5 的概率分布来说,J瀂濻瀁 有没有问题?很显然,我们先要看一看世界上其他 人群的分布情况,根据 GH-5 水平的分布情况来判断 J瀂濻瀁 是否是健康的。按照 平均值为 50,标准差为 25,我们可以给出一个概率密度函数的曲线,它表示了 GH-5 在世界范围内的分布情况,它符合正态分布。 正态分布的概率密度函数在画出来之后是一个类似钟型的连续分布。这个钟 型的形状,包括它的高低和胖瘦是由平均值和标准差来定义的。所以我们刚才提 到了 GH-5 的平均值是 50,标准差是 25。在任何一个点上,GH-5 的任何一个 取值的概率就可以通过上面的公式计算得到。 除了 GH-5 符合正态分布之外,其他很多现象也都符合正态分布。或者我们 可以理解为当数据的样本数非常大的时候,它的分布基本上就符合正态分布。 某个事件在某个取值范围内发生的概率就是这条曲线在这个取值范围内围
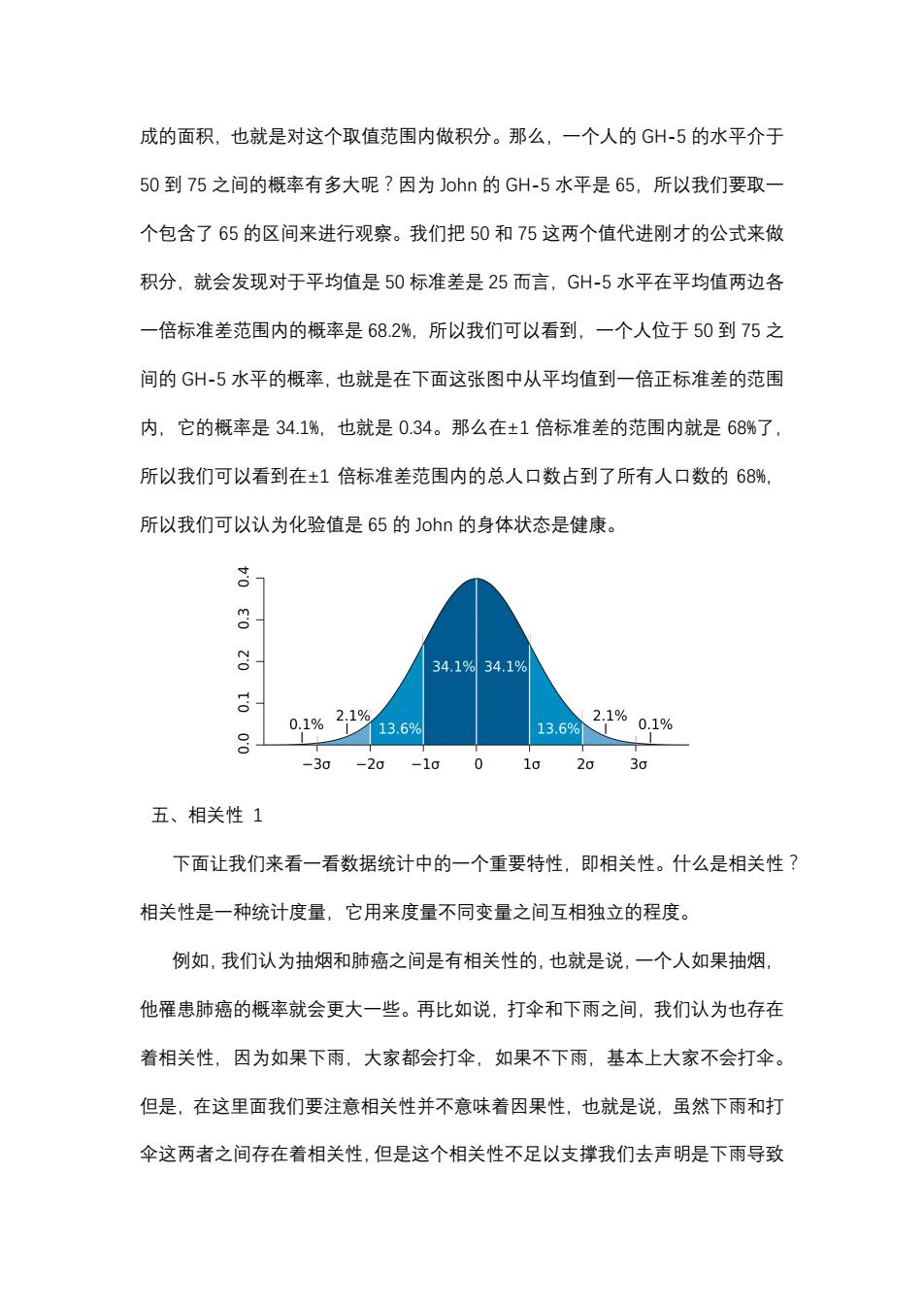
成的面积,也就是对这个取值范围内做积分。那么,一个人的GH-5的水平介于 50到75之间的概率有多大呢?因为John的GH-5水平是65,所以我们要取一 个包含了65的区间来进行观察。我们把50和75这两个值代进刚才的公式来做 积分,就会发现对于平均值是50标准差是25而言,GH-5水平在平均值两边各 一倍标准差范围内的概率是68.2%,所以我们可以看到,一个人位于50到75之 间的GH-5水平的概率,也就是在下面这张图中从平均值到一倍正标准差的范围 内,它的概率是34.1%,也就是0.34。那么在±1倍标准差的范围内就是68%了, 所以我们可以看到在±1倍标准差范围内的总人口数占到了所有人口数的68%, 所以我们可以认为化验值是65的John的身体状态是健康。 3 g 34.1%34.1% g 0.1% 2.1% 13.6% 13.6% 2.1%0.1% -30 -20 -10 0 10 20 30 五、相关性1 下面让我们来看一看数据统计中的一个重要特性,即相关性。什么是相关性? 相关性是一种统计度量,它用来度量不同变量之间互相独立的程度。 例如,我们认为抽烟和肺癌之间是有相关性的,也就是说,一个人如果抽烟 他罹患肺癌的概率就会更大一些。再比如说,打伞和下雨之间,我们认为也存在 着相关性,因为如果下雨,大家都会打伞,如果不下雨,基本上大家不会打伞。 但是,在这里面我们要注意相关性并不意味着因果性,也就是说,虽然下雨和打 伞这两者之间存在着相关性,但是这个相关性不足以支撑我们去声明是下雨导致
成的面积,也就是对这个取值范围内做积分。那么,一个人的 GH-5 的水平介于 50 到 75 之间的概率有多大呢?因为 J瀂濻瀁 的 GH-5 水平是 65,所以我们要取一 个包含了 65 的区间来进行观察。我们把 50 和 75 这两个值代进刚才的公式来做 积分,就会发现对于平均值是 50 标准差是 25 而言,GH-5 水平在平均值两边各 一倍标准差范围内的概率是 68.2%,所以我们可以看到,一个人位于 50 到 75 之 间的 GH-5 水平的概率,也就是在下面这张图中从平均值到一倍正标准差的范围 内,它的概率是 34.1%,也就是 0.34。那么在±1 倍标准差的范围内就是 68%了, 所以我们可以看到在±1 倍标准差范围内的总人口数占到了所有人口数的 68%, 所以我们可以认为化验值是 65 的 J瀂濻瀁 的身体状态是健康。 五、相关性 1 下面让我们来看一看数据统计中的一个重要特性,即相关性。什么是相关性? 相关性是一种统计度量,它用来度量不同变量之间互相独立的程度。 例如,我们认为抽烟和肺癌之间是有相关性的,也就是说,一个人如果抽烟, 他罹患肺癌的概率就会更大一些。再比如说,打伞和下雨之间,我们认为也存在 着相关性,因为如果下雨,大家都会打伞,如果不下雨,基本上大家不会打伞。 但是,在这里面我们要注意相关性并不意味着因果性,也就是说,虽然下雨和打 伞这两者之间存在着相关性,但是这个相关性不足以支撑我们去声明是下雨导致