
举例来说,对于刚才体重差异较大的一组人而言,他们的方差就分别是9, 8,291和292,与平均值150的差的平方累加以后再除以数据的个数4得到的 值就是20022.5。而对于体重比较接近的一组选手而言,他们的方差是分别是148, 152、150和150,与平均值150的差的平方累加以后再除以数据的个数4得到 的方差就是2。很显然,这两组人的方差的差异非常大,尽管他们的平均值相同。 通过方差我们就可以看出这两组数据不同的特性。方差越小,说明所有的数据的 分布范围越小,它们更接近于平均值,而方差越大,说明数据的分布范围越大, 它们更远离平均值。跟方差密切关联的另外一个指标是标准差,标准差就是对方 差的开方。在pandas中计算标准差的方式是在组装好的DataFrame对象上调用 std这个函数,它会计算每一列数据的标准差。 import pandas as pd df=pd.DataFrame({'c1:【1,2,3],c2':【1,2,100],'c3':l100,200,300】J,index=a',b',c'1) df.head() c1c2 c3 a11100 b22200 c3100300 df.std() 2 1.0000 56.8712 3 100.0000 dtype:float64 三、直方图&箱线图 直方图是一种常见的数据统计工具,用来计算对象的实例个数。例如,在下 面这个数据集中,这9个数据有三种不同的取值,分别是黄、红、绿。于是,我 们计算不同取值的实例的个数,得到了2个黄的,4个红的,以及3个绿的这样 的数据集,这就是最简单的直方图
举例来说,对于刚才体重差异较大的一组人而言,他们的方差就分别是 9, 8,291 和 292,与平均值 150 的差的平方累加以后再除以数据的个数 4 得到的 值就是 20022.5。而对于体重比较接近的一组选手而言,他们的方差是分别是 148, 152、150 和 150,与平均值 150 的差的平方累加以后再除以数据的个数 4 得到 的方差就是 2。很显然,这两组人的方差的差异非常大,尽管他们的平均值相同。 通过方差我们就可以看出这两组数据不同的特性。方差越小,说明所有的数据的 分布范围越小,它们更接近于平均值,而方差越大,说明数据的分布范围越大, 它们更远离平均值。跟方差密切关联的另外一个指标是标准差,标准差就是对方 差的开方。在 瀃濴瀁濷濴瀆 中计算标准差的方式是在组装好的 D濴瀇濴F瀅濴瀀濸 对象上调用 瀆瀇濷 这个函数,它会计算每一列数据的标准差。 三、直方图&箱线图 直方图是一种常见的数据统计工具,用来计算对象的实例个数。例如,在下 面这个数据集中,这 9 个数据有三种不同的取值,分别是黄、红、绿。于是,我 们计算不同取值的实例的个数,得到了 2 个黄的,4 个红的,以及 3 个绿的这样 的数据集,这就是最简单的直方图

在pandas中绘制直方图的方式很简单,只需要在装载好的DataFrame对象 上调用hist方法。例如,我们可以看到这个DataFrame包含C1和C2两列,这 两列完全由数字构成,所以在这个DataFrame上调用了hist方法之后,就会针 对这两列画出两个直方图,每一个直方图对应其中一列,表示了这一列中不同取 值的数据的个数。 c1 c2 df.hist() 11 array([[<matplotlib.axes.subplots.Axessubplot object at 0x102b97240>, 21 <matplotlib.axes.subplots.AxesSubplot object at 0x10b58e320>]],dtype=object) 31 cl 42 6 93 5 第二种常见的数据统计工具是箱线图。箱线图稍显复杂一些,它由一个方框 以及纵向贯穿它的竖线构成,这个方框的最下部表示数据的下四分位数,顶部表 示它的上四分位数,方框的范围就表达了四分位数的取值范围。在方框的中部有 一条贯穿方框的横线,表达的是整个数据集的中位值。在这条贯穿方框的纵线上, 上边缘表示的是整个数据集的最大值,下边缘表示的数据集的最小值。在方框中
在 瀃濴瀁濷濴瀆 中绘制直方图的方式很简单,只需要在装载好的 D濴瀇濴F瀅濴瀀濸 对象 上调用 濻濼瀆瀇 方法。例如,我们可以看到这个 D濴瀇濴F瀅濴瀀濸 包含 C1 和 C2 两列,这 两列完全由数字构成,所以在这个 D濴瀇濴F瀅濴瀀濸 上调用了 濻濼瀆瀇 方法之后,就会针 对这两列画出两个直方图,每一个直方图对应其中一列,表示了这一列中不同取 值的数据的个数。 第二种常见的数据统计工具是箱线图。箱线图稍显复杂一些,它由一个方框 以及纵向贯穿它的竖线构成,这个方框的最下部表示数据的下四分位数,顶部表 示它的上四分位数,方框的范围就表达了四分位数的取值范围。在方框的中部有 一条贯穿方框的横线,表达的是整个数据集的中位值。在这条贯穿方框的纵线上, 上边缘表示的是整个数据集的最大值,下边缘表示的数据集的最小值。在方框中
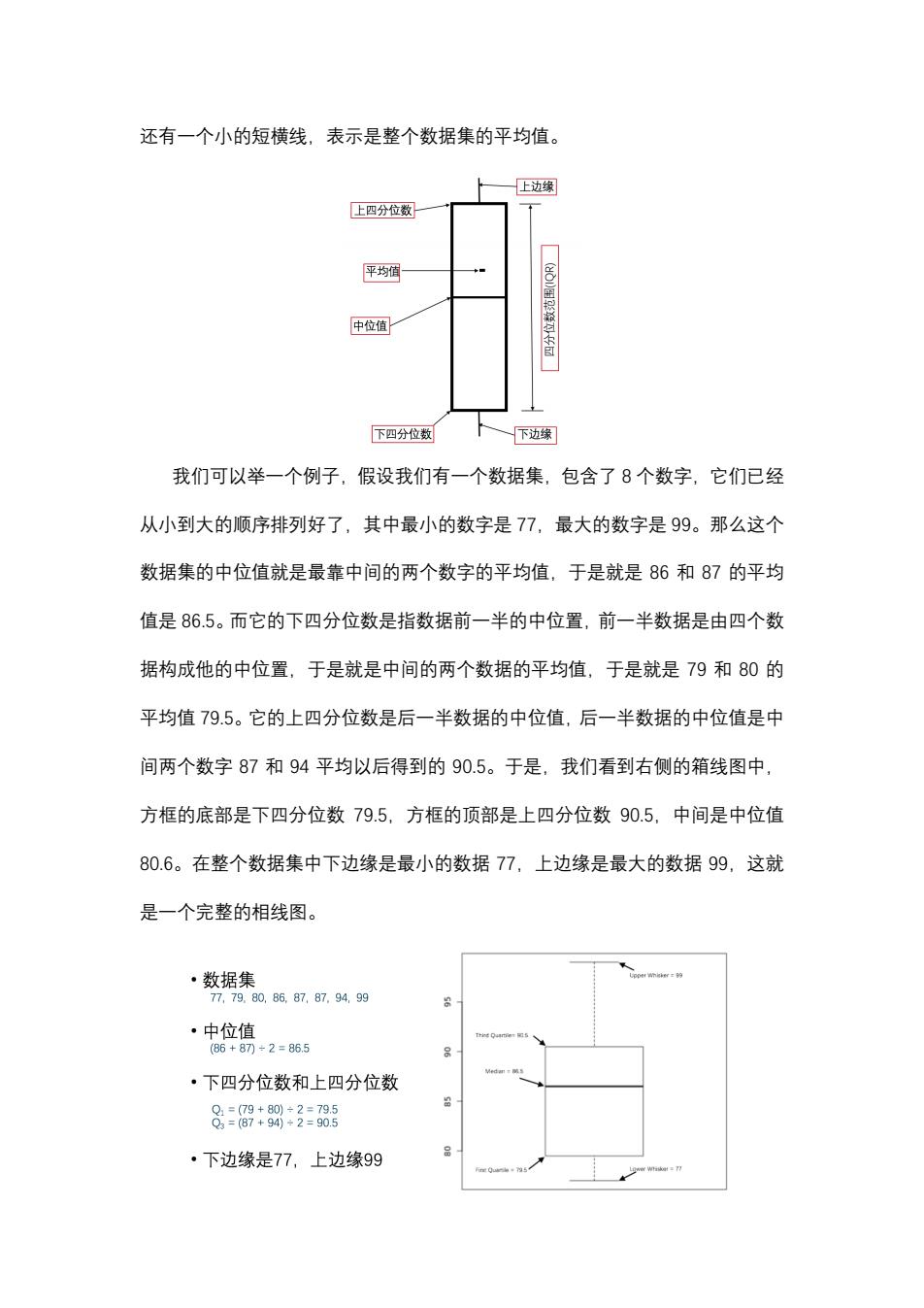
还有一个小的短横线,表示是整个数据集的平均值。 上边缘 上四分位数 平均值 中位值 下四分位数 下边缘 我们可以举一个例子,假设我们有一个数据集,包含了8个数字,它们已经 从小到大的顺序排列好了,其中最小的数字是77,最大的数字是99。那么这个 数据集的中位值就是最靠中间的两个数字的平均值,于是就是86和87的平均 值是86.5。而它的下四分位数是指数据前一半的中位置,前一半数据是由四个数 据构成他的中位置,于是就是中间的两个数据的平均值,于是就是79和80的 平均值79.5。它的上四分位数是后一半数据的中位值,后一半数据的中位值是中 间两个数字87和94平均以后得到的90.5。于是,我们看到右侧的箱线图中, 方框的底部是下四分位数79.5,方框的顶部是上四分位数90.5,中间是中位值 80.6。在整个数据集中下边缘是最小的数据77,上边缘是最大的数据99,这就 是一个完整的相线图。 ·数据集 77,79.80,8687,87.94.99 ·中位值 (86+87)+2=86.5 ·下四分位数和上四分位数 8=89+8*子:8 ·下边缘是77,上边缘99
还有一个小的短横线,表示是整个数据集的平均值。 我们可以举一个例子,假设我们有一个数据集,包含了 8 个数字,它们已经 从小到大的顺序排列好了,其中最小的数字是 77,最大的数字是 99。那么这个 数据集的中位值就是最靠中间的两个数字的平均值,于是就是 86 和 87 的平均 值是 86.5。而它的下四分位数是指数据前一半的中位置,前一半数据是由四个数 据构成他的中位置,于是就是中间的两个数据的平均值,于是就是 79 和 80 的 平均值 79.5。它的上四分位数是后一半数据的中位值,后一半数据的中位值是中 间两个数字 87 和 94 平均以后得到的 90.5。于是,我们看到右侧的箱线图中, 方框的底部是下四分位数 79.5,方框的顶部是上四分位数 90.5,中间是中位值 80.6。在整个数据集中下边缘是最小的数据 77,上边缘是最大的数据 99,这就 是一个完整的相线图
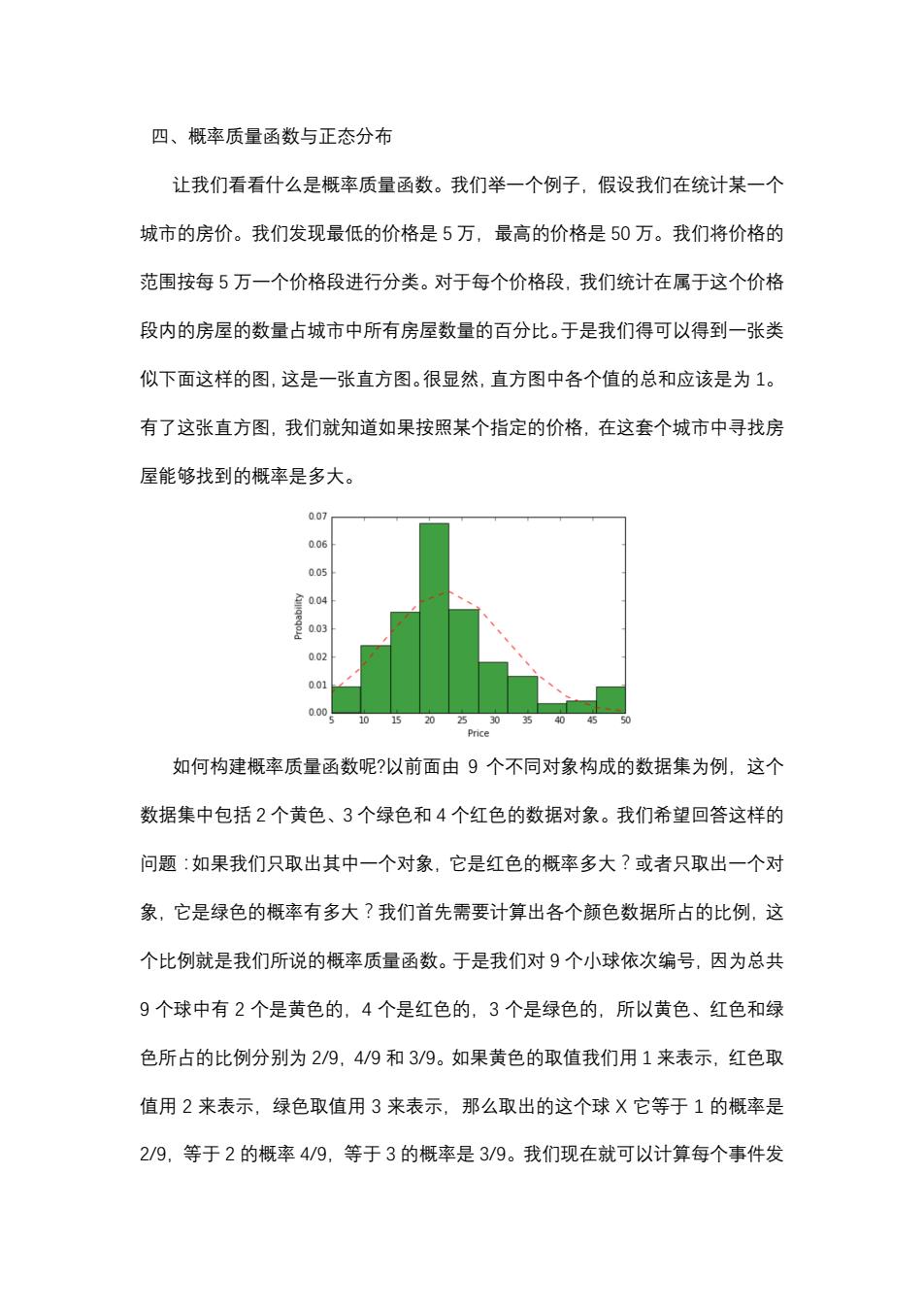
四、概率质量函数与正态分布 让我们看看什么是概率质量函数。我们举一个例子,假设我们在统计某一个 城市的房价。我们发现最低的价格是5万,最高的价格是50万。我们将价格的 范围按每5万一个价格段进行分类。对于每个价格段,我们统计在属于这个价格 段内的房屋的数量占城市中所有房屋数量的百分比。于是我们得可以得到一张类 似下面这样的图,这是一张直方图。很显然,直方图中各个值的总和应该是为1。 有了这张直方图,我们就知道如果按照某个指定的价格,在这套个城市中寻找房 屋能够找到的概率是多大。 0.07 006 0.05 室0.04 0.03 0.02 0.01 0.00 10 15 20 2530 5 40 Price 如何构建概率质量函数呢?以前面由9个不同对象构成的数据集为例,这个 数据集中包括2个黄色、3个绿色和4个红色的数据对象。我们希望回答这样的 问题:如果我们只取出其中一个对象,它是红色的概率多大?或者只取出一个对 象,它是绿色的概率有多大?我们首先需要计算出各个颜色数据所占的比例,这 个比例就是我们所说的概率质量函数。于是我们对9个小球依次编号,因为总共 9个球中有2个是黄色的,4个是红色的,3个是绿色的,所以黄色、红色和绿 色所占的比例分别为2/9,4/9和3/9。如果黄色的取值我们用1来表示,红色取 值用2来表示,绿色取值用3来表示,那么取出的这个球X它等于1的概率是 2/9,等于2的概率4/9,等于3的概率是3/9。我们现在就可以计算每个事件发
四、概率质量函数与正态分布 让我们看看什么是概率质量函数。我们举一个例子,假设我们在统计某一个 城市的房价。我们发现最低的价格是 5 万,最高的价格是 50 万。我们将价格的 范围按每 5 万一个价格段进行分类。对于每个价格段,我们统计在属于这个价格 段内的房屋的数量占城市中所有房屋数量的百分比。于是我们得可以得到一张类 似下面这样的图,这是一张直方图。很显然,直方图中各个值的总和应该是为 1。 有了这张直方图,我们就知道如果按照某个指定的价格,在这套个城市中寻找房 屋能够找到的概率是多大。 如何构建概率质量函数呢?以前面由 9 个不同对象构成的数据集为例,这个 数据集中包括 2 个黄色、3 个绿色和 4 个红色的数据对象。我们希望回答这样的 问题:如果我们只取出其中一个对象,它是红色的概率多大?或者只取出一个对 象,它是绿色的概率有多大?我们首先需要计算出各个颜色数据所占的比例,这 个比例就是我们所说的概率质量函数。于是我们对 9 个小球依次编号,因为总共 9 个球中有 2 个是黄色的,4 个是红色的,3 个是绿色的,所以黄色、红色和绿 色所占的比例分别为 2/9,4/9 和 3/9。如果黄色的取值我们用 1 来表示,红色取 值用 2 来表示,绿色取值用 3 来表示,那么取出的这个球 X 它等于 1 的概率是 2/9,等于 2 的概率 4/9,等于 3 的概率是 3/9。我们现在就可以计算每个事件发

生的概率了。 4 4 9 3 9 3-92-9 2-9 1-9 8 2 3 A 我们看到的概率质量函数和前面表示概率质量函数的直方图都有一个限制, 即,在图中我们看到的X的取值只能是离散的值,就像刚才我们看到的1、2、 3。但是,在很多情况下,我们实际的取值是实数,这也就意味着我们的取值可 能不是几个简单的离散值,而是在光滑的数轴上任意一个位置都可能出现的取值。 例如,我们的速度可以是4公里/每小时,也可以是4.5公里/每小时,或者是在 介于这两者之间的任意一个速度。再例如,我们每天要喝1公斤水或者2.5公斤 水,或者是介于这两个值之间的任意一个数量的水。 在这种情况下,用离散值表达的直方图和概率质量函数就有些不适用了,这 时候我们可以使用概率密度函数。在概率密度函数中,X可以是实数,也就是说, 将其在坐标系中画出来是一条光滑连续的曲线,而不是几个离散的点的取值。概 率密度函数有很多种,马上我们会讨论的是其中一种最常用的,叫做正态分布的 密度函数。由于概率密度函数是光滑连续的曲线,所以当我们在预测某个事件的 取值范围位于A和B之间时,实际上它的概率就是在A和B这个取值范围内计 算这条曲线围成的面积,也就是说对这条曲线在A到B的范围内做积分
生的概率了。 我们看到的概率质量函数和前面表示概率质量函数的直方图都有一个限制, 即,在图中我们看到的 X 的取值只能是离散的值,就像刚才我们看到的 1、2、 3。但是,在很多情况下,我们实际的取值是实数,这也就意味着我们的取值可 能不是几个简单的离散值,而是在光滑的数轴上任意一个位置都可能出现的取值。 例如,我们的速度可以是 4 公里/每小时,也可以是 4.5 公里/每小时,或者是在 介于这两者之间的任意一个速度。再例如,我们每天要喝 1 公斤水或者 2.5 公斤 水,或者是介于这两个值之间的任意一个数量的水。 在这种情况下,用离散值表达的直方图和概率质量函数就有些不适用了,这 时候我们可以使用概率密度函数。在概率密度函数中,X 可以是实数,也就是说, 将其在坐标系中画出来是一条光滑连续的曲线,而不是几个离散的点的取值。概 率密度函数有很多种,马上我们会讨论的是其中一种最常用的,叫做正态分布的 密度函数。由于概率密度函数是光滑连续的曲线,所以当我们在预测某个事件的 取值范围位于 A 和 B 之间时,实际上它的概率就是在 A 和 B 这个取值范围内计 算这条曲线围成的面积,也就是说对这条曲线在 A 到 B 的范围内做积分